Лекция 2. Введение: Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы

Введение: Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы. Его положение в пространстве полностью определяется значением угла поворота вокруг оси оси вращения из некоторого условно выбранного начального положения этого тела. Чем дальше отстоят от оси вращения тела рассматриваемые его точки, тем большие пути они проходят за один и тотже промежуток времени. Соответственно тем больше его скорости. Поэтому для описания вращательного движения тела неудобно пользоваться такими понятиями кинематики точки, как перемещение, пройденный путь, скорость и ускорение точки. В этом случае мы вводим угловые характеристики. Основная часть: Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Для характеристики вращения тела вокруг оси служит угловая скорость. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

ω =

Вектор w направлен вдоль оси вращения по правилу правого винта.

Здесь d j - вектор элементарного (бесконечно малого) угла поворота тела за время dt, направленный вдоль оси вращения также по правилу правого винта.

За время dt точка, перемещаясь по дуге окружности, проходит путь

dS = R dφ.

Поэтому модуль скорости точки

v =

или в векторном виде

v= [ ω, R ].

Периодом вращения называется промежуток времени Т, в течение которого тело, совершает один оборот вокруг оси вращения (поворачивается на угол j = 2p):

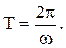
Частотой вращения называется число оборотов, совершаемых телом за единицу времени:

Для характеристики изменения вектора угловой скорости тела вводится вектор углового ускорения тела, равный первой производной от его угловой скорости по времени.

Вектор углового ускорения направлен вдоль оси вращения: при ускоренном движении вектор ε сонаправлен ω, при замедленном – противоположен ему.

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Между движением твеpдого тела вокpуг неподвижной оси и движением отдельной матеpиальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Пpи pешении задач полезно пользоваться этой аналогией. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вpащения твеpдого тела. Кооpдинате s соответствует угол, линейной скоpости v - угловая скоpость, линейному (касательному) ускоpению а - угловое ускоpение. Пpиведем пpимеp того, как можно пользоваться аналогией между поступательным и вpащательным движениями. Известно, что pавноускоpенное движение описывается фоpмулами

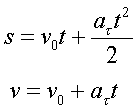
По аналогии можно записать соответствующие фоpмулы для pавноуско­pенного вpащения твеpдого тела:

Выводы: параметрами, описывающими кинематику вращательного движения, являются следующие угловые характеристики: вектор элементарного поворота тела, угловая скорость, угловое ускорение.

Лекция 3

Законы динамики

Динамика занимается изучением движения тел в связи с действующими на них силами. Силой F, действующей на тело, называется мера взаимодействия его с окружающими телами или полями. Любое тело оказывает сопротивление при попытках привести его в движение или изменить скорость. Это свойство называется инертностью. Мера инертности тела называется массой. Масса является также и мерой гравитационного взаимодействия тел. Импульсом тела называется векторная величина, обладающая свойством сохранения и равная произведению массы тела на его скорость:

p = m v.

Первый закон Ньютона. Существуют такие системы отчета, называемые инерциальными, в которых тело, не подверженное внешнему воздействию, находится в покое или движется равномерно и прямолинейно. Системы отчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными.

Второй закон Ньютона. Скорость изменения импульса материальной точки равна действующей на него силе:

если m = const, то m a = F.

Если на материальную точку действует несколько сил F ₁, F ₂, …, F _n, то их равнодействующая сила является суммой всех этих сил:

Этот экспериментальный факт получил название принципа суперпозиции сил.

Третий закон Ньютона. Две материальные точки действуют друг на друга с силами, которые численно равны и направлены в противоположные стороны вдоль прямой, соединяющей эти точки

где F ₁₂ – сила, действующая на первую материальную точку со стороны второй; F ₂₁ – сила, действующая на вторую точку со стороны первой. Эти силы приложены к разным материальным точкам.

Третий закон Ньютона не распространяется на силы инерции.

Поиск по сайту: