 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Закон сохранения импульса. Центр масс
Любую совокупность материальных тел называют механической системой. Силы, действующие между телами системы, называют внутренними, а со стороны тел, не включенных в данную систему, внешними. Если действием внешних тел на тела данной системы можно пренебречь, то систему называют замкнутой.
Из второго закона Ньютона для системы материальных точек следует:

где 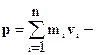 импульс всей системы, F внешн. - равнодействующая всех внешних сил, действующих на нее. Внутренние силы исключаются третьим законом Ньютона. Таким образом, производная по времени от импульса системы материальных точек равна геометрической сумме всех внешних сил, действующих на систему.
импульс всей системы, F внешн. - равнодействующая всех внешних сил, действующих на нее. Внутренние силы исключаются третьим законом Ньютона. Таким образом, производная по времени от импульса системы материальных точек равна геометрической сумме всех внешних сил, действующих на систему.
В замкнутой системе выполняется закон сохранения импульса:

Центром масс системы материальных точек называется точка С, радиус вектор r c которой равен

где r i - радиус-вектор i-й материальной точки, а  - масса всей системы.
- масса всей системы.
Скорость центра масс

Т.к. импульс системы равен произведению массы всей системы на скорость ее центра масс:  то:
то:

где 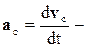 ускорение центра масс. Таким образом, центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
ускорение центра масс. Таким образом, центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
Лекция 4
Энергией называется мера различных форм движения и взаимодействия. Количественной характеристикой процесса обмена энергией между взаимодействующими телами является работа силы А.
Элементарной работой dA силы F на малом перемещении d r точки приложения силы называется скалярное произведение силы F на перемещение d r:

где dS = | d r | - элементарный путь, α - угол между силой F и элементарным перемещением d r, FS =Fcosα - проекция силы F на направление d r. Тогда полная работа на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути, т.е. выражается интегралом: 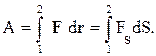
Если зависимость FS задана графически, то работа измеряется площадью криволинейной трапеции S112S2.
Мощность -работа, совершаемая за единицу времени:
N = 
В механике различают два вида энергии: кинетическую и потенциальную. Кинетической энергией Wk называется энергия механического движения системы. Изменение кинетической энергии материальной точки происходит под действием приложенной к ней силы F и равно работе, совершаемой этой силой:
dWk=dA
Используя второй закон Ньютона  , получаем:
, получаем:

 Откуда:
Откуда:
 k
k 
Кинетическая энергия зависит только от массы и скорости тела, т.е., кинетическая энергия системы есть функция состояния ее движения.
Потенциальная энергия - механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Силы, работа которых не зависит от формы траектории, а определяется только положениями начальной и конечной точек, называются консервативными (например, гравитационные и упругие силы). Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения.
Введем понятие потенциальной энергии как некоторой функции состояния взаимодействующих тел (их взаимного расположения) и будем считать, что работа консервативной силы равна убыли потенциальной энергии:

где АК – работа консервативных сил; Wп - потенциальная энергия.
Соответственно, работа консервативных сил при малом изменении конфигурации системы
dA = ‑ dWП.
С другой стороны
dA = F d r.
Следовательно, потенциальная энергия материальной точки

где С – постоянная интегрирования, которая определяется из начальных и граничных условий. То есть потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это не отражается на физических законах, так как они содержат или разность потенциальных энергий в двух положениях тела, или производную Wп по координатам.
Связь между силой и потенциальной энергией имеет вид:
F = ‑ grad WП,
где символом grad обозначена сумма

В общем случае градиентом скалярной функции φ (grad φ) называется вектор, совпадающий по направлению с осью, вдоль которой функция φ возрастает с наибольшей скоростью; модуль градиента φ равен изменению этой функции на единицу длины при перемещении вдоль данной оси.
Потенциальная энергия тела в поле силы тяжести с напряженностью g равна:
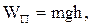
где высота h отсчитывается от нулевого уровня, для которого Wп=0.
Потенциальная энергия в поле тяготения равна:

где r - расстояние между центрами масс, при условии, что потенциальная энергия в центральном поле тяготения равна нулю при удалении взаимодействующих тел на бесконечно большое расстояние друг от друга.
Потенциальная энергия деформированной пружины равна:
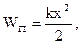
считая, что потенциальная энергия пружины равна нулю при х = 0, т.е. когда пружина не деформирована.
Допустим, что в системе действуют консервативные и диссипативные силы. Работа всех сил А12 при переходе системы из положения 1 в положение 2 равна приращению ее кинетической энергии:
А12=Wk2-Wk1.
Но эту работу можно представить в виде суммы работы консервативных сил А12 кон. и работы диссипативных сил А12 дис.. Первая работа может быть выражена через убыль потенциальной энергии системы:
А12 кон.=Wп1-Wп2.
Поэтому
А12=Wп1-Wп2+ А12 дис.
Приравнивая это выражение к приращению кинетической энергии, получим:
Wk2-Wk1=Wп1-Wп2+ А12 дис, или
W2-W1= А12 дис,
где W=Wk+Wп - полная механическая энергия системы.
Итак, закон сохранения энергии: в замкнутых системах, где действуют только консервативные силы полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно.
В системах с диссипативными силами механическая энергия постепенно уменьшается за счет преобразования в другие виды энергии (например, в энергию беспорядочного движения молекул). Строго говоря, все системы в природе являются диссипативными. Однако, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.
Примером применения законов сохранения импульса и энергии является удар абсолютно упругих и неупругих тел.
Абсолютно упругий удар -это взаимодействие двух тел, в результате которого механическая энергия сохраняется. Рассмотрим центральные удары абсолютно упругих шаров. В этом случае скорости шаров до удара v1 и v2 направлены вдоль прямой, соединяющей их центры. Эта прямая называется линией удара. Скорости шаров после столкновения v1' и v2' находим из законов сохранения импульса и энергии:

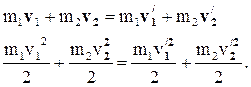
Решая эту систему уравнений, получим:

 Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу. Если массы шаров m1 и m2, их скорости до удара v1 и v2, то используя закон сохранения импульса, можно записать
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу. Если массы шаров m1 и m2, их скорости до удара v1 и v2, то используя закон сохранения импульса, можно записать

где v – скорость движения шаров после удара. Тогда 
При неупругом ударе в соударяющихся телах происходят различные процессы (пластические деформации, трение и др.), в результате которых происходит потеря кинетической энергии, превращающейся в тепловую или другие виды энергии. Эту потерю можно определить по разности кинетической энергии до и после удара:

Лекция 5
При изучении вращения твердых тел, как мера инертности, используется понятие момента инерции.
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу
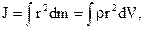
где ρ - плотность тела в данной точке, а интегрирование производится по всему объему тела V.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции JC относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями

Значения моментов инерции для некоторых тел приведены в таблице:
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиусом R | То же |  mR2 mR2
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину |  m l 2 m l 2
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 
|
| Шар радиусом R | Ось проходит через центр шара | 
|
Кинетическая энергия вращения
Рассмотрим абсолютно твердое тело вращающееся около неподвижной оси Z, проходящей через него. Разобьем это тело на маленькие объемы с элементарными массами m1, m2, … mn, находящимися на расстоянии r1, r2, … rn от оси вращения.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi описывают окружности различных радиусов ri и имеют различные линейные скорости vi.
Угловая скорость вращения этих объемов одинакова:

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:


где J – момент инерции тела относительно оси вращения Z.
Таким образом, кинетическая энергия вращающегося тела

В случае плоского движения тела, например, цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

где m – масса катящегося тела;
vC – скорость центра масс тела;
JC – момент инерции тела относительно оси, проходящей через его центр масс;
w – угловая скорость тела.
Поиск по сайту: