Лекция 9

Молекулярная физика – раздел физики, в котором рассматриваются зависимости агрегатных состояний и свойств тел от их строения, взаимодействия между частицами и от характера движения частиц.

Согласно молекулярно-кинетическим представлениям, любое тело (твердое, жидкое или газообразное) состоит из мельчайших обособленных частиц, называемых молекулами. Эти частицы находятся в беспорядочном, хаотическом движении, интенсивность которого зависит от температуры тела. Такое движение молекул называется тепловым.

Существует два способа описания процессов, происходящих в макроскопических телах (то есть телах, состоящих из очень большого числа частиц – атомов или молекул): статистический и термодинамический.

Статистическая физика – раздел физики, посвященный изучению свойств макроскопических тел исходя из свойств частиц, образующих тело и взаимодействий между ними. В совокупном поведении частиц, координаты и импульсы которых случайны в любой момент времени, проявляются особые статистические закономерности.

Термодинамика – раздел физики, изучающий общие свойства макроскопических тел и протекающие в них процессы, не вдаваясь в микроскопическую природу тел. Термодинамический метод основан на анализе условий и количественных соотношений при различных превращениях энергии, происходящих в системе. Термодинамика основывается на законах, установленных опытным путем: первом и втором началах термодинамики.

Термодинамической системой называется система, состоящая из такого большого числа частиц, находящихся в беспорядочном (тепловом) движении, что поведение отдельных частиц не влияет на состояние системы в целом.

Замкнутой системой называется термодинамическая система, не способная к обмену энергией с внешней средой путем совершения работы. Адиабатной системой называется термодинамическая система, не способная к обмену энергией с другими системами путем теплообмена.

Термодинамическими параметрами (параметрами состояния) называются макроскопические величины, являющиеся усредненным выражением микроскопических характеристик частиц термодинамической системы. К ним относят давление, объем, температуру, концентрацию и другие.

Давлением р называется сила, действующая на единицу площади:

,

где dF_n - модуль нормальной силы, действующей на малый участок поверхности площадью dS. В СИ давление измеряется в Н/м² (эта единица называется паскалем, Па). На практике часто пользуются внесистемными единицами:

1 ат – техническая атмосфера, 1 ат = 9,81·10⁴ Па.

1 атм – нормальная атмосфера, 1 атм = 1,013·10⁵ Па = 760 мм рт.ст.

1 мм рт. ст. = 133,3 Па.

Объемом V системы называется часть пространства, занимаемая термодинамической системой. В СИ объем измеряется в кубических метрах (м³). Часто используется внесистемная единица – литр: 1 л=10^{-3 м3}.

Понятие температуры имеет смысл только для равновесных состояний системы.

Равновесным состоянием называется состояние термодинамической системы, при котором параметры состояния не изменяются с течением времени.

Температура системы Т, находящейся в равновесном состоянии, является мерой интенсивности теплового движения атомов, молекул и других частиц, образующих систему. Средняя кинетическая энергия поступательного движения одной молекулы выражается через температуру с помощью постоянной Больцмана к=1,38·10^-23 Дж/К:

.

Постоянная Больцмана является коэффициентом пропорциональности между кинетической энергией одной молекулы и температурой и показывает, сколько Дж в одном Кельвине.

В СИ принята термодинамическая температурная шкала, где единицей измерения является кельвин (К). Величина одного кельвина равна величине одного градуса по шкале Цельсия. Градус равен одной сотой разности температур замерзания и кипения воды при нормальном атмосферном давлении. Термодинамическая температура и температура по шкале Цельсия связаны соотношением

Т=t + 273,15⁰С.

Плотностью называется масса, содержащаяся в единице объема системы. В СИ плотность измеряется в кг/м³.

.

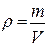Концентрацией называется число частиц в единице объема вещества. В СИ концентрация измеряется в м ^—3:

.

Термодинамическим процессом называется переход системы из одного состояния в другое. Процесс, протекающий при неизменном одном параметре, называется изопроцессом. Примерами изопроцессов являются:

1 изотермический процесс, при котором температура системы не меняется (Т=const);

2 изохорный процесс, происходящий при постоянном объеме системы (V=const);

3 изобарный процесс, происходящий при постоянном давлении в системе (p=const);

4 адиабатный процесс, происходящий без теплообмена между системой и внешней средой (dQ=0).

Идеальным газом называется термодинамическая система, частицы которой имеют пренебрежимо малый объем по сравнению с объемом системы, не взаимодействуют друг с другом на расстоянии, а столкновения происходят как абсолютно упругие.

Уравнение, связывающее давление, объем и температуру газа для данной его массы, называется уравнением состояния:

f (p, V, T) = const.

Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона:

pV = ,

где R =8,31 Дж/моль∙К, - универсальная газовая постоянная; М – молярная масса газа, 1 моль – количество вещества, содержащее число молекул, равное числу Авогадро: N_A =6,02 ∙10²³ моль^-1. Если m₀ – масса одной молекулы, то молярная масса

М=m₀ N_A.

Тогда масса произвольного количества вещества ν равна

m=Mν=m₀N_Aν,

где - число молей вещества.

Употребляется ещё одна форма уравнения состояния. ПостояннаяБольцмана k связана с универсальной газовой постоянной:

k= =1,38∙10^-23 Дж/К.

Уравнение Менделеева – Клапейрона получает вид:

p= = ,

где N=νN_A – число молекул газа; n = -концентрация молекул.

Лекция 10

Числом степеней свободы i тела называется наименьшее число независимых координат, которые необходимо задать для того, чтобы полностью определить положение тела в пространстве.

Молекула одноатомного газа имеет три степени свободы поступательного движения. Молекула двухатомного газа, кроме трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения. Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных.

i=i_пост + i_вращ.

Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная ½ kT. Следовательно, средняя кинетическая энергия молекулы, имеющей i степеней свободы, равна

.

К изучению свойств газов применяется статистический метод. Пусть газ заключен в сосуд, имеющий форму параллелепипеда с основанием S и высотой ,где V – скорость молекулы, 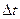– время. Молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения со стенками сосуда абсолютно упругие.

Давление, производимое молекулами газа на стенки сосуда, обусловлено столкновениями их со стенками сосуда. Молекула, движущаяся перпендикуляр-

но площадке S, при каждом соударении передает ей импульс m₀ V-(-m₀ V)=2m₀ V, где m₀ – масса молекулы. За время 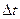площадки S достигнут только те молекулы, которые заключены в объе­ме параллелепипеда. Число этих молекул равно nSV t (n – концентрация молекул).

Необходимо учитывать, что реально молекулы дви­жутся к площадке S под разными углами. Поэтому хаотическое движение молекул заменяется движением вдоль трех взаимно перпендикулярных направлений, причем половина молекул движется вдоль данного направления в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет . При столкновении с площадкой эти молекулы передадут ей импульс:

.

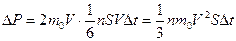Тогда давление газа, оказываемое им на стенку сосуда,

.

В действительности скорости теплового движения молекул различны как по направлению, так и по модулю. Поэтому нужно рассматривать среднюю квадратичную скорость

,

где V_i – скорость i -й молекулы.

Если ввести эту скорость в выражение для давления, то

.

Так как n = ,

.

Итак, уравнение кинетической теории для давления идеального газа имеет вид:

,

где 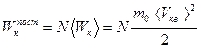- кинетическая энергия поступательного движения всех молекул N.

Из сравнения с уравнением Менделеева-Клапейрона следует, что

.

Лекция 11

Внутренняя энергия U включает в себя энергию всевозможных видов движения и взаимодействия всех частиц (молекул, атомов и др.), образующих рассматриваемую систему, кроме кинетической энергии системы как целого и потенциальной энергии во внешнем силовом поле. Внутренняя энергия идеального газа равна сумме кинетических энергий беспорядочного движения всех молекул. Для молей идеального газа внутренняя энергия равна

.

Внутренняя энергия является однозначной функцией состояния термодинамической системы, т.е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние).

Первое начало термодинамики является законом сохранения энергии применительно к механической и тепловой энергии: теплота, сообщаемая системе Q, расходуется на изменение внутренней энергии системы dU и на совершение системой работы против внешних сил А:

Q= dU+dA.

В этом выражении dU является полным дифференциалом, dQ и А не являются полными дифференциалами, т.к. ни теплота, ни работа не являются функциями состояния.

Вычислим работу, связанную с расширением или сжатием газа. Пусть газ находится в цилиндре, который закрыт подвижным поршнем, имеющим площадь S. Под действием приложенной внешней силы F поршень опустился на расстояние dx, сжав при этом газ. Газ будет сжиматься до тех пор, пока сила F не уравновесится силой, действующей на поршень со стороны газа и равной pS, где р – давление газа. Работа dА, затраченная на перемещение поршня на расстояние dx:

,

где 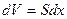- изменение объема газа.

Работа, совершаемая при конечных изменениях объема, вычисляется путем интегрирования:

.

На графике работа численно равна площади фигуры под этой кривой.

Теплоемкостью вещества называется физическая величина, равная количеству теплоты , которое нужно сообщить веществу для изменения его температуры на единицу:

.

Удельной теплоемкостью вещества называется физическая величина, равная количеству теплоты, которое нужно сообщить единице массы вещества для изменения его температуры на единицу:

.

Молярной теплоемкостью называется физическая величина, равная количеству теплоты, которое нужно сообщить одному молю вещества для изменения его температуры на единицу:

.

Удельная теплоемкость связана с молярной соотношением:

.

Первое начало термодинамики можно представить в виде:

.

Лекция 12

Первое начало термодинамики для различных изопроцессов идеальных газов принимает вид:

1. В изохорном процессе (V =const) , поэтому dU= Q, т.е.

,

где – молярная теплоемкость газа при постоянном объеме.

4. В изобарном процессе (р = const) , где - молярная теплоемкость газа при постоянном давлении. Элементарная работа .

dQ=dU+dA,

.

Отсюда следует, что 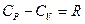, или .

3. В изотермическом процессе (Т =const) . Вся теплота, сообщаемая газу, расходуется на совершение газом работы против внешних сил: dQ=dA,

.

Теплоемкость газа в изотермическом процессе , т.к. , а .

4. В адиабатном процессе .Первое начало термодинамики имеет вид: , т.е. система совершает работу за счет убыли внутренней энергии.

.

Теплоемкость при адиабатном процессе .

Связь между параметрами состояния в адиабатном процессе:

,

,

,

где - показатель адиабаты.

Политропными процессами называются процессы, в которых теплоемкость имеет любое, но постоянное на протяжении всего процесса значение. Все рассмотренные ранее процессы являются частными случаями политропного процесса. Уравнение политропы имеет вид:

,

где n – показатель политропы. При Т=const n=1; p=const n=0; V=const n= .

Лекция 13

Круговым процессом или циклом называется такая совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние.

Тепловым двигателем (машиной) называется круговой процесс (цикл), с помощью которого возможно многократное превращение тепла в работу. Принцип действия теплового двигателя приведен на рисунке. От термостата с более высокой температурой Т₁, называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой Т₂, называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа А=Q₁-Q₂. Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине.

Рабочим телом называется тело, совершающее круговой процесс и обменивающееся энергией с другими телами.

Термический коэффициент полезного действия для кругового процесса .

Циклом Карно называется цикл, обладающий максимальным к.п.д, состоящий из двух изотерм 1-2, 3-4 и двух адиабат 2-3, 4-1. В качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

При изотермическом процессе U=const, поэтому количество теплоты Q₁, полученное газом от нагревателя, равно работе расширения А₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

.

При адиабатном расширении 2-3 работа расширения А₂₃ совершается за счет изменения внутренней энергии:

.

При изотермическом сжатии количество теплоты Q₂, отданное газом холодильнику, равно работе сжатия А₃₄:

.

При адиабатном сжатии: .

Работа, совершаемая в результате кругового процесса,

A=A₁₂+A₂₃+A₃₄+A₄₁=Q₁ –Q₂.

Термический к.п.д. цикла Карно

.

Лекция 14

Обратимым процессом называется термодинамический процесс, совершаемый системой, если после него можно возвратить систему и все взаимодействовавшие с ней тела в их начальные состояния таким образом, чтобы в других телах не возникло каких-либо остаточных изменений, т.е. процесс, протекающий в прямом и обратном направлении через последовательность одних и тех же состояний. Процесс, не удовлетворяющий этим условиям, является необратимым. Всякий обратимый процесс является равновесным.

Приведенным количеством теплоты называется отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела. Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно . В любом обратимом круговом процессе

,

следовательно, - полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние:

.

Энтропией называется функция состояния, дифференциалом которой является . Неравенство Клаузиуса называется математической формулировкой второго начала термодинамики:энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов):

.

Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

.

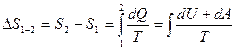Энтропия определяется с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий.

Так как , , то

или ,

т.е. изменение энтропии идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1 2.

Для адиабатного процесса () .

Для изотермического процесса (Т=const) .

Для изохорного процесса (V=const) .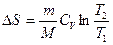

В статистической физике энтропия связывается с термодинамической вероятностью состояния системы. Термодинамической вероятностью или статистическим весом W состояния системы называется число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, W ≥1). Согласно Больцману, энтропия системы и термодинамическая вероятность связаны между собой: 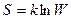, где k – постоянная Больцмана. То есть энтропия является мерой неупорядоченности системы.

Второе начало термодинамики определяет направление протекания термодинамических процессов. Второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает. По Больцману, возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Укажем другие формулировки второго начала термодинамики:

1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, результатом которого является самопроизвольная передача теплоты от менее нагретого тела к более нагретому.

Третье начало термодинамики: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

Лекция 15

Благодаря беспорядочному движению и взаимным столкновениям молекулы газа распределяются по скоростям так, что среди них имеются как очень быстрые, так и очень медленные молекулы. Такое распределение подчиняется статистическому закону Максвелла.

.

В таком виде распределение Максвелла справедливо для любых систем, частицы которых находятся в беспорядочном тепловом движении, то есть для термодинамических систем.

Функция распределения молекул по скоростям f (V) определяет относительное число молекул , скорости которых лежат в единичном интервале около скорости V, т.е. . Величина имеет смысл вероятности: это вероятность того, что любая из молекул газа, содержащихся в единице объема, обладает скоростью, лежащей в интервале от V до V+ΔV. Поэтому f (V) называют плотностью вероятности. Графически вид функции распределения Максвелла представлен на рисунке. Функция распределения обращается в нуль при V= 0 и при V = . Скорость V_в, которой соответствует максимум кривой распределения Максвелла, называется наиболее вероятной скоростью.

.

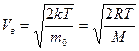С увеличением температуры газа максимум кривой смещается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями, уменьшается, а доля молекул с большими скоростями увеличивается.

Средней арифметической скоростью называется отношение суммы всех скоростей всех молекул в единице объема к числу молекул в единице объема. Чтобы ее найти, нужно долю молекул 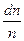, обладающих некоторой скоростью V, умножить на эту скорость и просуммировать по всем скоростям. Так как скорость изменяется непрерывно, то суммирование заменяется интегрированием.

,

.

Если термодинамическая система находится в внешнем силовом поле, то распределение частиц системы зависит от разности потенциальных энергий в контактирующих частях системы. Например, зависимость давления атмосферного воздуха от высоты над поверхностью Земли описывается барометрической формулой

.

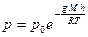Здесь p₀ – давление газа на высоте h= 0.

Если использовать уравнение состояния идеального газа в форме p=nkT, то барометрическая формула приводит к соотношению

n= .

Если учесть, что mgh=ΔW_п – потенциальная энергия молекулы в поле тяготения вблизи поверхности Земли, то формулу можно переписать в виде:

.

Здесь ΔW_п – разность потенциальных энергий частиц с концентрацией n и n₀.

Это выражение называется законом Больцмана для распределения частиц термодинамической системы во внешнем потенциальном поле.

Поиск по сайту: