Момент силы. Уравнение динамики вращательного движения твердого тела

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F:

Модуль момента силы

где a - угол между r и F;

d=r sin a - кратчайшее расстояние между линией действия силы и точкой О – плечо силы.

Вектор М перпендикулярен плоскости, в которой лежат вектора r и F, и направлен в ту сторону, в которую будет двигаться винт с правой нарезкой, если его головку вращать в том же направлении, в каком необходимо поворачивать вектор r для совпадения с вектором F по кратчайшему пути.

Моментом силы относительно неподвижной оси Z называется проекция на эту ось вектора М момента силы отно­сительно произвольной точки О на данной оси Z.

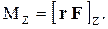
Найдем выражение для работы при вращении тела. Пусть си­ла F приложена в точке В, находящейся от оси Z на расстоянии r, и a - угол между направлением силы и радиусом-вектором r. При повороте тела на бесконечно малый угол dj точка В проходит путь

dS = r dj и работа

dA = F_SdS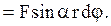

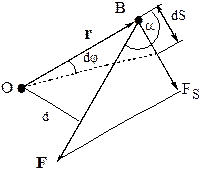Так как момент силы относительно оси Z, то можно записать:

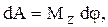
Работа при вращении тела идет на увеличение его кинетической энергии:

но

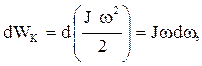
поэтому

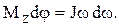
Учитывая, что получаем: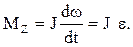

Это уравнение представляет собой уравнение динамики вращательного дви­жения твердого тела относительно неподвижной оси: произведение момента инерции твер­дого тела относительно неподвижной оси на угловое ускорение равно моменту внешних сил относительно той же оси.

В любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые при вращении тела не изменяют своей ориентации в пространстве без действия на них внешних сил. Они называются главными осями инерции.

Если ось Z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

где J – главный момент инерции тела.

Лекция 6

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением

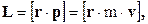
где r – радиус-вектор, проведенный из точки О в точку А, p = m v – импульс материальной точки.

Модуль вектора момента импульса

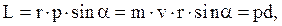
где a - угол между векторами r и p, d – плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси Z называется скалярная величина L_Z, равная проекции на эту ось вектора момента импульса, определенного относите­льно произвольной точки О данной оси.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

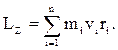
Используя формулу: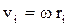

получим: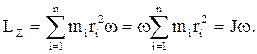

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость

.

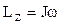Продифференцируем это уравнение по времени:

Производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. В векторном виде уравнение имеет вид:

В замкнутой системе момент внешних сил:

откуда

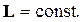
Данное выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Лекция 7

Рассмотpим, как пpеобpазуются кооpдинаты и вpемя события пpи пеpеходе от одной ИСО к дpугой. Рассмотpим две ИСО: К и К ', у котоpых кооpдинатные оси х и х' напpавлены вдоль их относительной скоpости v, а оси y, y' и z,z' соответственно паpаллельны. Пусть в момент t = 0 начала кооpдинат систем совпадали. На pис. 5.7 изобpажены такие системы.

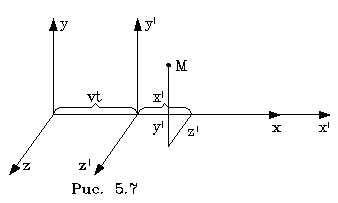
Если бы одновpеменность событий была абсолютной и никаких pелятивистских эффектов не было, то пpеобpазования кооpдинат и вpемени некотоpого события М имели бы вид:

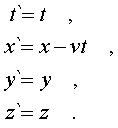
(5.12)
Эти пpеобpазования имеют место в классической физике и называются пpеобpазованиями Галилея.
Второй закон Ньютона можно использовать в неинерциальных системах отчета, если учесть силы инерции. Силы инерции F _ин должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение a', каким оно обладает в неинерциальной системе отчета, то есть:

m a' = F + F _ин.

При поступательном движении системы отчета с ускорением а₀

F _ин = -m a₀.

Во вращающейся с угловой скоростью ω системе отcчета на покоящееся тело действует сила инерции, называемая центробежной силой инерции:

F _ц = -mω² R.

Во вращающейся с угловой скоростью ω системе отcчета на движущееся тело со скоростью v' действует сила Кориолиса:

F _k = 2m [ v',ω ].

Лекция 8

Поиск по сайту: