 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Арифметика комплексных чисел
Для цепей переменного тока, так же как и для цепей постоянного тока, справедливы законы Кирхгофа. Поэтому все основанные на их использовании методы расчета цепей применимы и для цепей переменного тока. Однако токи, сходящиеся в узле, так же как и напряжения, действующие на элементах контура, суммируются геометрически, т. е. складываются соответствующие векторы.
В этом случае электротехническая задача может быть сведена к задаче геометрической, к расчету треугольников.
Такой метод требует точного построения векторной диаграммы, что невозможно без проведения предварительных расчетов токов и напряжений приемника.
Символический метод расчета электрических цепей основан на описании векторов комплексными числами, что позволяет заменить геометрическое сложение векторов суммированием комплексных чисел, соответствующих векторам.
В данный момент времени положение вращающегося вектора на плоскости можно описать двумя методами:
1) задавая его проекции на оси координат.
2) задавая его длину (в математике длина вектора называется модулем) и угол, который вектор образует с положительным направлением горизонтальной оси.
| А |
| +j |
| -j |
| +1 |
| -1 |
| b |
| a |
| j |
| Рис. 12. Вращающийся вектор на комплексной плоскости |
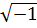 и называется мнимой единицей (рис. 12).
и называется мнимой единицей (рис. 12).
Положение вектора на комплексной плоскости можно записать (рис. 12):
 .
.
Сомножители 1 перед a и j перед b указывают, на какие оси спроектирован вектор. Подчеркивание снизу символа A означает комплексную величину.
Такая форма записи называется алгебраической и удобна для проведения операций сложения и вычитания. Например, требуется сложить два вектора:  и
и  . Имеем:
. Имеем:
 .
.
Из рисунка 12видно, что проекции вектора A на оси равны:
a=Acosj, b=Asinj,
где А – модуль или длина вектора A (обратите внимание, что этот символ не имеет никаких подчеркиваний).
Тогда:
A =Acosj + jAsinj = A(cosj + jsinj).
Такая форма записи комплексного числа называется тригонометрической.
Учитывая, что cosj + jsinj = ejj, получаем:
A =A ejj.
Такая форма записи комплексного числа называется показательной, она удобна для умножения и деления. Например, требуется перемножить и разделить векторы: A =5 ej30, В =10 e-j90. Имеем:
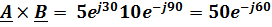 ,
,
 .
.
Для перехода от показательной формы записи к алгебраической и, наоборот, от алгебраической к показательной воспользуемся треугольником, выделенным на рисунке 12, и применим теорему Пифагора:

Например:

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ АКТИВНОГО СОПРОТИВЛЕНИЯ R,
КОНДЕНСАТОРА С И ИНДУКТИВНОСТИ L
Рассмотрим цепь с активным, индуктивным и емкостным сопротивлениями, включенными последовательно (рис.13).

Рис.13. Последовательное соединение элементов цепи.
Для анализа схемы разложим напряжение сети U на три составляющие:
UR - падение напряжения на активном сопротивлении,
UL - падение напряжения на индуктивном сопротивлении,
UC - падение напряжения на емкостном сопротивлении.
Ток в цепи I будет общим для всех элементов:


Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I.
Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном - отстает от него на 90°.
Графически это можно показать на векторной диаграмме (рис. 14).

Рис. 14. Векторная диаграмма
Изображенные выше три вектора падения напряжений можно геометрически сложить в один (рис. 15).

Рис. 15. Сложение трех векторов напряжения.
В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак.
Интересным является режим, когда = 0.
В этом случае

Такой режим работы схемы называется резонансом напряжений.
Полное сопротивление при резонансе напряжений имеет минимальное значение:
 , и при заданном напряжении U ток I может достигнуть максимального значения.
, и при заданном напряжении U ток I может достигнуть максимального значения.
Из условия  определим резонансную частоту
определим резонансную частоту

Явления резонанса напряжений широко используется в радиотехнике и в отдельных промышленных установках.
Задача3. Электрическая цепь, показанная на рис. 3.1. питается от источника синусоидального тока с частотой 200 Гц и напряжением 120 В. Дано: R = 4 Ом, L = 6,37 мГн, C = 159 мкФ.
Вычислить ток в цепи, напряжения на всех участках, активную, реактивную, и полную мощности. Построить векторную диаграмму, треугольники сопротивлений и мощностей.

Рис. 3.1.
1. Вычисление сопротивлений участков и всей цепи
Индуктивное реактивное сопротивление
XL = 2πf L = 2×3,14×200×6,37·10-3 Ом.
Емкостное реактивное сопротивление
XC = 1 / (2πf C) = 1 / (2×3,14×200×159·10-6) Ом.
Реактивное и полное сопротивления всей цепи:
X = XL - XC = 3 Ом;  Ом.
Ом.
2. Вычисление тока и напряжений на участках цепи
Ток в цепи
I = U / Z = 120 / 5 А.
Напряжения на участках:
U1 = R I = 96 В; U2 = XL I = 192 В; U3 = XC I = 120 В.
3. Вычисление мощностей
Активная мощность
P = R I2 = U1 I = 2304 Вт.
Реактивные мощности:
QL = XL I2 = U2 I = 4608 ВАр; QC = XC I2 = U3 I = 2880 ВАр.
Полная мощность цепи
 ВА.
ВА.
4. Расчет цепи методом комплексных чисел
Запишем в комплексном виде сопротивление каждого элемента и всей цепи
R = 4ej0° = 4 Ом; XL = 8e+j90° = j8 Ом; XC = 5e-j90° = -j5 Ом.
Z = R + j(XL - XC) = 4 + j(8 - 5) Ом.
На комплексной плоскости в масштабе: в 1 см – 2 Ом, построим треугольник сопротивлений (рис. 3.2. а).

Рис. 3.2.
Из треугольника определим величину полного сопротивления Z и угол фазового сдвига φ
 Ом;
Ом;
 .
.
В показательной форме полное сопротивление всей цепи запишется в виде
Z = Ze+jφ = 5e+j37°Ом.
Примем начальную фазу приложенного к цепи напряжения за нуль и определим по закону Ома ток в данной цепи
Í = Ú / Z = 120e+j0° / 5e+j37° А.
Следовательно, в данной цепи ток отстает по фазе от напряжения на угол φ. Зная величину тока I, определим мощности для отдельных элементов и всей цепи.
P = 2304 Вт; QL = 4608 ВАр; QC = 2880 ВАр.
 .
.
Треугольник мощностей в масштабе: в 1 см – 1000 Вт (ВАр); (ВА), построим (рис. 3.2. б) на основе выражения для полной мощности
S2 = P2 + (QL - QC)2.
Для построения векторных диаграмм по току и напряжениям примем начальную фазу тока равной нулю, т.к. ток I в данной схеме является одним и тем же для всех элементов в цепи.
Í = Ie+j0° / 24e+j0°А.
Запишем выражения для напряжений в комплексной форме
Ú1 = R Í = 96e+j0° В; Ú2 = XL Í = 192e+j90°В;
Ú3 = XC Í = 120e-j90° В; Ú = Z Í = 120e+j37° В.
Выберем масштабы для векторной диаграммы: в 1 см – 6 А; в 1 см – 50 В. Векторная диаграмма напряжений строится на основе второго закона Кирхгофа для данной цепи
Ú = Ú1 + Ú2 + Ú3.
Векторная диаграмма цепи показана на рис. 3.2. в. При последовательном соединении элементов построение диаграммы начинают с вектора тока Í, по отношению к которому ориентируются вектора напряжений на участках цепи: напряжение на активном сопротивлении Ú1 совпадает с ним по направлению, напряжение на индуктивности Ú2 опережает его на 90°, на емкости отстает на 90°. Полное напряжение Ú строится как их векторная сумма.
Поиск по сайту: