 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Расчет разветвленной электрической цепи с несколькими источниками питания
Одним из методов расчета сложных электрических цепей является метод контурный токов
При расчете электрических цепей этим методом в основе лежит II закон Кирхгофа, который гласит: алгебраическая сумма ЭДС, действующих в контуре, равна алгебраической сумме падений напряжений в том же контуре:
 ;
;
При расчете цепей методом контурных токов предполагается, что в каждом контуре протекает независимый расчетный ток, который называется контурным.
При расчете методом контурных токов количество уравнений определяется числом независимых контуров или по формуле:
p = m - (n - 1),
где m – число ветвей, n – число узлов.
Ветвь – участок цепи, в любом сечении которого течет один и тот же ток.
Узел – точка цепи соединения 3-х и более ветвей.
Контур – любой путь вдоль электрической цепи, начинающегося и заканчивающегося в одной и той же точке. Контур электрической цепи, содержащий хотя бы один элемент принадлежащий только ему, называется независимым.
При расчете рекомендуется соблюдать следующую последовательность:
1. Выделить независимые контуры.
2. На схеме указать номера независимых контуров и указать направление их обхода (направление обхода всех контуров лучше выбирать одним и тем же).
3. Указать направления контурных токов в каждом независимом контуре (чтобы избежать ошибок направления контурных токов должны совпадать с направлением обхода контуров).
4. Для всех независимых контуров составить уравнения по второму закону Кирхгофа: ЭДС считаются положительными, если их направление совпадает с направлением обхода контура; падение напряжения IkiRi считается положительным, если направление контурного тока совпадает с направлением обхода контура.
5. Решить составленную систему линейных уравнений.
6. Произвести проверку правильности решения системы линейных уравнений.
7. По вычисленным значениям контурных токов найти величины токов в ветвях и их направление: ток и его направление в наружной ветви соответствует контурному току; ток в смежных ветвях определяем, как алгебраическую сумму контурных токов, протекающих в этой ветви, и его направление будет совпадать с направлением большего контурного тока.
8. Составить баланс мощностей.
Рассмотрим алгоритм решения на примере цепи, изображенной на рисунке 2.1.
1. По признакам, данным в определении независимого контура, можно выделить следующие независимые контуры: a-b-c-g-a (контур I), c-d-e-g-c (контур II), a-g-e-f-a (контур III).

Рис.2. 1. Расчетная схема
2. Направление обхода указывается стрелкой снаружи схемы. Направление обхода по контурам выбрали совпадающим с направлением движения часовой стрелки.
3. Направления контурных токов в независимых контурах выбрали такими же, как и направления обхода контуров, по часовой стрелке.
1. По второму закону Кирхгофа для каждого независимого контура составляем уравнения (ЭДС считаются положительными, если их направление совпадает с направлением обхода контура; падение напряжения IkiRi считается положительным, если направление контурного тока совпадает с направлением обхода контура). Обратите внимание, что в смежных ветвях протекают два контурных тока, причем они направлены в разные стороны:
Контур I a-b-c-g-a: E1=IК1R1+ IК1R6+ IК1R5–IК2R6– IК3R5;
Контур II c-d-e-g-c: –E2 +E3=IК2R2+ IК2R3+ IК2R6–IК3R3– IК1R6;
Контур III a-g-e-f-a: - E3 +E4=IК3R3+ IК3R4+ IК3R5–IК1R5– IК2R3.
Сгруппировав слагаемые, получим систему уравнений:
E1=IК1 (R1+R6+ R5)–IК2R6– IК3R5; (1)
–E2 +E3=IК2 (R2+ R3+ R6)–IК3R3– IК1R6; (2)
- E3 +E4=IК3 (R3+ R4+R5)–IК1R5– IК2R3. (3)
2. Полученная система уравнений может быть решена любым известным методом. Не рекомендуется вести решение подстановкой, так как при этом ошибки допускаются чаще, чем при решении другими способами.
Для удобства записи введем следующие обозначения:
a1,a2,a3 – коэффициенты при контурном токе IК1;
b1,b2,b3 – коэффициенты при контурном токе IК2;
c1,c2,c3 – коэффициенты при контурном токе IК3;
d1,d2,d3 – свободные члены в правой части системы уравнений.
Тогда систему линейных уравнений можно переписать следующим образом:
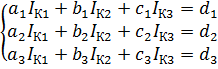
При ручном расчете решение полученной системы уравнений можно найти по формулам Крамера:
 ,
,
где

Для вычисления определителя третьего порядка удобно приписать к нему справа два первых столбца, тогда произведения элементов, вычеркнутых в таблице сплошной линией, будут складываться, а произведения элементов, вычеркнутых пунктирной линией, вычитаться, например для вычисления Δ:
 ,
,
Δ1, Δ2, Δ3 вычисляются аналогично.
При составлении таблиц элементов и вычислении определителей следите за знаками элементов и знаками их произведений.
При расчете на ЭВМ составляется матрица коэффициентов:
 .
.
Если в исходных уравнениях некоторые неизвестные контурные токи отсутствуют, в матрицу коэффициентов проставляются соответствующие нули.
3. После вычисления контурных токов проведите первую проверку правильности расчета. Исходные уравнения должны превращаться в тождество при подстановке в них полученных значений контурных токов.

Рис.2. 2. Расчетная схема после расчета контурных токов
Значения контурных токов, полученные в результате расчета, могут быть положительными и отрицательными. Если контурный ток получился отрицательным, то меняем его направление на схеме на противоположное. При этом контурный ток, протекающий через резисторы, также меняет направление (рис. 2). Допустим контурные токи Ik1, Ik2 положительные, а контурный ток Ik3 – отрицательный. На схеме (рис. 2.2) направления контурных токов Ik1, Ik2 оставляем прежними, а направление контурного тока Ik3 меняем на противоположное. Следовательно, токи в наружных ветвях цепи (в нашем примере на рис. 2.2 ветви E1-R1, E2-R2, E4-R4) равны по величине и направлению соответствующим контурным токам. На схеме около каждого резистора укажите действительное направление тока в нем. Номер тока указывается в соответствии с номером резистора.
В смежных ветвях, принадлежащих одновременно двум контурам (в нашем примере ветви E3-R3, R5, R6), протекают одновременно по два контурных тока. Поэтому действительные токи в ветвях определяют как алгебраическую сумму контурных токов, протекающих по этим ветвям (см. рис. 2.2). Если контурные токи в резисторе направлены в противоположные стороны, то для нахождения действительных значений токов в этих ветвях необходимо из большего контурного тока, протекающего в данной ветви, вычесть меньший контурный ток, протекающий в этой же ветви, и принять направление большего контурного тока. Если контурные токи направлены в одну и ту же сторону, то для определения тока в ветви их необходимо сложить и направление полученного тока будет совпадать с направлением этих расчетных контурных токов.
Допустим, что  , причем Ik1, Ik2 - положительные, а Ik3 – отрицательный, тогда токи в ветвях будут равны:
, причем Ik1, Ik2 - положительные, а Ik3 – отрицательный, тогда токи в ветвях будут равны:
I1 =Ik1; I2 =Ik2; I4 = Ik3; I3 =Ik2 + Ik3; I5 =Ik1 + Ik3; I6 =Ik1 - Ik2.
На схеме указываем направления токов в ветвях:
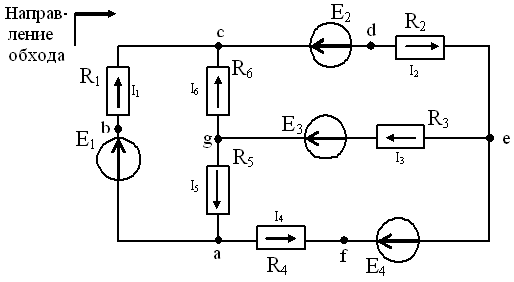
Рис. 2.3. Расчетная схема после расчета токов в ветвях
4. Правильность расчета проверяют, составляя баланс мощностей. Согласно закону сохранения энергии, мощность, отдаваемая источниками, должна быть равна мощности, поглощаемой приемниками, т. е.:
 или
или 
Перед произведением EI знак «+» ставится, если направление тока совпадает с направлением ЭДС. Знак «-», если направление тока не совпадает с направлением ЭДС.

Если равенство выполняется, то расчет правильный. При правильно рассчитанных токах расхождение мощностей не должно превышать 2%.
Еще одним методом расчета является метод непосредственного применения первого и второго законов Кирхгофа.
В качестве примера рассмотрим цепь, схема которой приведена на рис. 2.4. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа (1.3) составляют уравнения для (n–1) узлов. Недостающие m–(n–1) уравнения получают по второму закону Кирхгофа составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.
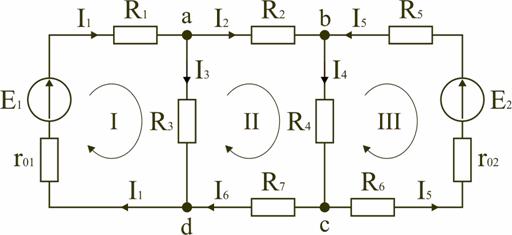
Рис. 2.4
1. Обозначение токов во всех ветвях. Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендеются, чтобы направление токов совпадало с направлением ЭДС.
2. Составление уравнений по первому закону Кирхгофа. Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения:
узел a: I1−I2−I3=0;
узел b: I2−I4+I5=0;
узел c: I4−I5+I6=0.
3. Составление уравнений по второму закону Кирхгофа. Необходимо составить 6–3=3 уравнения. В схеме на рис.2. 4 выбираем контура I, II, III и для них записываем уравнения:
контур I: E1=I1(r01+R1)+I3R3;
контур II: 0=I2R2+I4R4+I6R7−I3R3;
контур III: −E2=−I5(r02+R5+R6)−I4R4.
4. Решение полученной системы уравнений и анализ результатов. Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя.
5. Проверка правильности расчетов. Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений:
узел d: I3+I6−I1=0
внешний контур схемы: E1−E2=I1(r01+R1)+I2R2−I5(r02+R5+R6)+I6R7.
Независимой проверкой является составление уравнения баланса мощностей с учетом режимов работы элементов схемы с ЭДС:
 .
.
Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.
Поиск по сайту: