Пример 40.2

Проверить опорный план, полученный в примере 40.1, на оптимальность. Найти оптимальный план.

Решение.

Полученный план является невырожденным, так как число занятых клеток таблицы , где – число поставщиков (), – число потребителей (). Проверим найденный план на оптимальность с помощью метода потенциалов.

Для этого каждому поставщику поставим в соответствие потенциал , а каждому потребителю – потенциал .

Для каждой занятой клетки таблицы должно выполняться условие , а для каждой свободной – (, ).

Составим таблицу потенциалов (табл. 40.3).

Таблица 40.3

Таблица потенциалов для плана

	– 13	– 10

Для каждой свободной клетки вычислим оценки 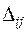по формуле:

.

Данный план не является оптимальным так как оценка и оценка . План необходимо улучшить, перераспределив груз по циклу (табл. 40.4).

Таблица 40.4

Улучшение плана путем перераспределения груза по циклу

План	-Q 180			+Q
	+Q		-Q 20
			+Q	-Q

В клетку, для которой положительная оценка 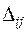наибольшая ставим знак «+», и далее расставляем чередуя знаки «–» и «+» во всех вершинах цикла. Количество груза, которое необходимо перераспределить по этому циклу, определяется как величина, наименьшая из поставок, стоящая в клетках со знаком «–»:

.

Таким образом, нам необходимо перераспределить по замкнутому циклу 20 единиц груза.

После проделанной операции получаем новый план 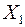(табл. 40.5), для которого стоимость перевозки изменяется на величину и равна

.

Таблица 40.5

План перевозок

План

Проверим план на оптимальность с помощью метода потен-циалов (табл. 40.6).

Таблица 40.6

Таблица потенциалов для плана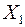

План не является оптимальным, так как имеется две положительные оценки и . Определяем, что , то есть, необходимо сделать поставку в клетку , .

Перераспределение груза по циклу представлено в табл. 40.7.

Таблица 40.7

Улучшение плана путем перераспределения груза по циклу

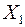
План	-Q 160	+Q
+Q	-Q

По представленному циклу перераспределяем груз в количестве единиц. Получаем новый план (табл. 40.8) и проверяем его на оптимальность (табл. 40.9).

Таблица 40.8

План перевозок

План				20

Таблица 40.9

Таблица потенциалов для плана

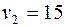
Все оценки 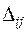положительны. Следовательно, получен оптимальный план. Общая стоимость перевозок по этому плану минимальна и равна:

.

Решим теперь эту задачу методом минимального элемента матрицы стоимостей (табл. 40.10).

Таблица 40.10

Исходный опорный план

Поставщики	Потребители	Запасы,
Потребности,

Полученный план является невырожденным, так как число занятых клеток таблицы , где – число поставщиков (), – число потребителей ().

Сравнивая полученные результаты решения задачи двумя методами, можем сделать вывод, что найденный план является оптимальным и задача решена.

Следовательно, минимальная стоимость перевозки груза в размере 10280 достигается при .

Поиск по сайту: