Метод потенциалов. Одним из наиболее эффективных и распространенных методов определения оптимальности плана ТЗ является метод потенциалов

Одним из наиболее эффективных и распространенных методов определения оптимальности плана ТЗ является метод потенциалов. Впервые он был предложен в 1949 г. Л. В. Канторовичем и М. К. Гавуриным.

Позже на базе общих идей линейного программирования аналогичный метод был предложен Дж. Данцигом.

Этот метод позволяет проверить, является ли данный опорный план оптимальным, и если нет, то определить такой путь улучшения этого плана, по которому каждая следующая итерация дает опорный план, которому отвечает меньшее значение целевой функции.

Следует заметить что, при решении транспортной задачи может оказаться, что число занятых клеток меньше, чем . В этом слу­чае задача имеет вырожденное решение.

Для возможного исключения вырожденного решения целесообразно поменять местами поставщиков и потребителей или ввести в свободную клетку с наименьшим тарифом нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и каждом столбце было не менее одной занятой клетки.

Найденное исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: ес­ли опорное решение транспортной задачи является оптималь­ным, то ему соответствует система действительных чи­сел и , удовлетворяющих условиям 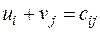для заня­тых клеток и для свободных клеток.

Числа и называют потенциалами. В распределитель­ную таблицу добавляют строку и столбец .

Потенциалы и находят из равенства 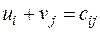, спра­ведливого для занятых клеток. Одному из потенциалов дает­ся произвольное значение, например 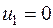, тогда остальные потенциалы определяются однозначно. Так, если известен по­тенциал , то ; если известен потенциал , то .

Обозначим . Эту оценку называют оценкой свободных клеток. Если 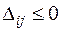, то опорное решение является оптимальным. Если хотя бы одна из оценок , то опор­ное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.

Алгоритм метода потенциалов

1. Строится система потенциалов, отвечающая найденному опорному решению. Для этого решают систему уравнений , для , которая имеет множество решений.

Для нахождения частного решения системы одному из потен-циалов (обычно тому, которому отвечает наибольшее число занятых клеток) задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам: если известен потенциал то если ; и, если известен потенциал , то если

2. Проверяется выполнение условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формуле и те из них, которые больше нуля, записывают в левые нижние углы клеток.

Если для всех свободных клеток , то найден оптимальный план и задача решена. Остается только вычислить значение целевой функции. Если же имеется одна или несколько клеток с положительной оценкой, то опорное решение не является оптимальным.

3. Осуществляется переход к новому опорному плану. Для этого находят клетку таблицы, которой соответствует самая большая положительная оценка ; строится цикл, который включает в свой состав данную клетку и часть клеток, занятых опорным решением.

4. Определяется цикл (контур) перераспределения и объем груза, который можно перераспределить в соответствии с этим циклом. Клетка, которой отвечает самая большая положительная оценка, вместе с другими из занятых клеток должна образовывать замкнутый контур.

Поворот можно осуществлять под прямым углом только в занятых клетках (или в условно занятых, если опорный план вырожденный) (рис. 17.1).

Всем угловым клеткам цикла присваивают соответствующий знак.

Свободную клетку, в которую необходимо осуществить поставку, обозначают знаком «+», следующую угловую клетку цикла – знаком «–», дальше – знаком «+». Знаки расставляем до тех пор, пока не вернемся к исходной клетке.

Рис. 40.1. Типы контуров перераспределения груза

Для определения объема груза , который можно перераспределить по этому циклу, рассматривают те угловые клетки, которые вошли в цикл перевозок со знаком «–», и по ним определяют наименьший объем груза. Это и есть то количество груза, которое необходимо перераспределить по данному циклу.

5. Количество груза в каждой угловой клетке цикла меняют на величину , причем так, что перевозка во всех клетках со знаком «–» уменьшается на , а во всех клетках со знаком «+» увеличивается на (в клетках, которые не обозначены никакими знаками, объем груза не меняется).

Вследствие перераспределения груза получают новый опорный план, по которому целевая функция имеет значение, меньше предыдущего на . Этот план снова проверяют на оптимальность методом потенциалов.

Процесс продолжают до тех пор, пока не будет получен оптимальный план.

Поиск по сайту: