Границы применимости Ньютоновской механики

1. выполняются только в инерциальных системах отсчета
2. неприменимы к явлениям микромира
3. нельзя применить для объектов, скорость движения которых сравнима со скоростью света

1. Импульс системы. Закон сохранения импульса.

Механическая система и её состояние. Внутренние и внешние силы. Замкнутая система. Импульс системы. Закон сохранения импульса. Центр масс. Центр масс системы и способы его нахождения. Уравнение движения центра масс. Реактивное движение. Уравнение Мещерского и формула Циолковского.

Импульс – векторная величина, являющаяся мерой механического движения тела. В классической механике импульс равен: 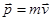. В системе СИ импульс измеряется в кг*м/с.

Механическая система и её состояние. Совокупность тел называют механической системой. Примером механической системы может быть любой механизм: тепловоз с вагонами, Солнце с планетами, а также любое тело, если его рассматривать как совокупность отдельных частиц. Если в условиях рассматриваемой задачи формой, размерами и внутренней структурой тел, входящих в механическую систему, можно пренебречь, то их рассматривают как систему материальных точек.

Внутренние и внешние силы. В классической механике масса является аддитивной

величиной: суммарная масса механической системы равна сумме масс входящих в систему тел (материальных точек). Силы, действующие между телами (материальными точками), которые составляют данную систему, называют внутренними. Силы, действующие на тела системы со стороны других тел, которые не входят в систему, называются внешними.

Замкнутая система. Такой системой называется механическая система, на каждое из тел которой не действуют внешние силы. В изолированной системе проявляются внутренние силы, т.е. силы взаимодействия между телами, входящими в систему.

Центр масс. Для описания движения каждой точки можно использовать законы Ньютона. Однако, особенно если система состоит из большого количества точек, это описание весьма громоздкое и не учитывает поведения системы в целом. Движение системы как целого удобно рассматривать, используя понятие центра масс. Центром масс системы материальных точек называется такая точка, радиус-вектор () которой равен отношению суммы произведений масс всех точек и их радиус-векторов к суммарной массе системы. 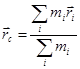, радиус-вектор i-й точки.

Импульс механической системы равен: , где масса системы равна сумме всех масс системы i. Считая массу системы неизменной, получим: . Импульс системы равен произведения массы системы на скорость её центра масс.

Уравнение движения центра масс: 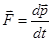. Центр масс системы движется, как МТ, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил действующих на систему. Из закона сохранения импульса вытекает, что центр масс замкнутой системы движется прямолинейно и равномерно или остаётся неподвижным.

Закон сохранения импульса. При любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы остаётся постоянным. Закон сохранения полного импульса изолированной системы – универсальный закон природы.

Реактивное движение. Движение, которое происходит как результат отделения от тела какой-либо части или как результат присоединения к телу другой части.

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

; V – конечная (после выброса всего топлива)скорость аппарата, I - удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива); M1 - начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо); M2 - конечная масса летательного аппарата (полезная нагрузка + конструкция). Из нее следует, что конечная скорость, приобретаемая ракетой при отсутствии внешних сил, не зависит от закона изменения массы и ограничена только отношением начальной и конечной масс ракеты.

Уравнение Мещерского – это уравнение движения тел переменной массы, , левая часть представляет собой произведение массы и ускорения ракеты. Следовательно, справа должна стоять сумма сил, которые действуют на ракету.(F – внешняя сила).

Случай, когда внешние силы отсутствуют (F=0) т.е. система ракета + выбрасываемые газы является замкнутой. На основе закона сохранения импульса можно утверждать, что суммарный импульс системы остается неизменным. В этом случае получаем соотношение , на основе которого можно сделать вывод о том, что ракета получает такое же приращение импульса, как и выбрасываемые газы, только в противоположном направлении. Причиной изменения импульсов отдельных частей замкнутой системы могут быть только внутренние силы, действующие между ними. Та-

ким образом, на ракету со стороны газов действует реактивная сила:

1. Работа и мощность силы

Работа и мощность, единицы их измерения. Работа силы тяжести, силы упругости, силы трения. Механическая энергия системы и закон её сохранения. Энергия. Кинетическая энергия и её связь с работой внешних сил. Потенциальная энергия и её связь с силой поля. Механическая энергия. Закон сохранения механической энергии.

Работа и мощность. Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой (A), совершаемой постоянной силой (F) называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения

. Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы. Если направление силы, приложенной к телу, перпендикулярно направлению перемещения тела, то работа в этом случае равна нулю

Мощность (N) Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: 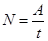. Мгновенная мощность в данный момент времени: . В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Поиск по сайту: