 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кинематика прямолинейного движения
Электромагнитное поле - это особая форма материи, посредством которой осуществляется взаимодействие между заряженными частицами. Представляет собой взаимосвязанные переменные электрическое поле и магнитное поле. Взаимная связь электрического и магнитного полей заключается в том, что всякое изменение одного из них приводит к появлению другого: переменное электрическое поле, порождаемое ускоренно движущимися зарядами (источником), возбуждает в смежных областях пространства переменное магнитное поле, которое, в свою очередь, возбуждает в прилегающих к нему областях пространства переменное электрическое поле, и т. д. Таким образом, электромагнитное поле распространяется от точки к точке пространства в виде электромагнитных волн, бегущих от источника. Благодаря конечности скорости распространения электромагнитное поле может существовать автономно от породившего его источника и не исчезает с устранением источника (например, радиоволны не исчезают с прекращением тока в излучившей их антенне).
Известно, что около проводника, по которому протекает ток, возникают одновременно электрическое и магнитное поля. Если ток не меняется во времени, эти поля не зависят друг от друга. При переменном токе магнитное и электрическое поля связаны между собой, представляя единое электромагнитное поле.
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию.
Частота электромагнитного поля — это число колебаний поля в секунду. Единицей измерения частоты является герц (Гц) — частота, при которой совершается одно колебание в секунду.
Длина волны — это расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах.
Поляризация — это явление направленного колебания векторов напряженности электрического поля или напряженности магнитного поля.
Электромагнитное поле обладает определённой энергией и характеризуется электрической и магнитной напряжённостью, что необходимо учитывать при оценке условий труда.
В целом общий электромагнитный фон состоит из источников естественного (электрические и магнитные поля Земли, радиоизлучения Солнца и галактик) и искусственного (антропогенного) происхождения (телевизионные и радиостанции, линии электропередачи, электробытовая техника). Источниками электромагнитных излучений также служат радиотехнические и электронные устройства, индукторы, конденсаторы термических установок, трансформаторы, антенны, фланцевые соединения волноводных трактов, генераторы сверхвысоких частот и др.
Современные геодезические, астрономические, гравиметрические, аэрофотосъёмочные, морские геодезические, инженерно-геодезические, геофизические работы выполняются с использованием приборов, работающих в диапазоне электромагнитных волн, ультравысокой и сверхвысокой частот, подвергая работающих опасности с интенсивностью облучения до 10 мкВт/см2.
Электромагнитное излучение подразделяется на:
радиоволны (начиная со сверхдлинных),
терагерцовое излучение,
инфракрасное излучение,
видимый свет,
ультрафиолетовое излучение,
рентгеновское излучение и жёсткое (гамма-излучение).
Электромагнитное излучение способно распространяться практически во всех средах. В вакууме (пространстве, свободном от вещества и тел, поглощающих или испускающих электромагнитные волны) электромагнитное излучение распространяется без затуханий на сколь угодно большие расстояния, но в ряде случаев достаточно хорошо распространяется и в пространстве, заполненном веществом (несколько изменяя при этом своё поведение).
Вибратор Герца (диполь Герца, антенна Герца) — простейшая система для получения электромагнитных колебаний, электрический диполь, дипольный момент которого быстро изменяется во времени. Представляет собой развёрнутый колебательный контур с минимальной ёмкостью и индуктивностью. Технический эквивалент — небольшая антенна, размер которой много меньше длины волны. Первые опыты с этим вибратором были осуществлены Герцем в 1888 году.
Герц использовал медные стержни с металлическими шарами на концах, в искровой промежуток которых включалась катушка Румкорфа. Если подать на такую конструкцию высокое напряжение, в промежутке проскочит искра, а в вибраторе возникнут колебания с периодом меньше, чем время горения искры. Длина электромагнитных волн примерно в два раза превышает размеры самого вибратора. Наименьший из применявшихся Герцем вибраторов (0,26 м) позволял получить колебания с частотой порядка 5·108 Гц, что соответствует длине волны в 0,6 м. Герц также помещал вибраторы в фокусе вогнутых зеркал для получения направленных плоских волн.
С помощью металлических зеркал и асфальтовой призмы Герц убедился в том, что законы отражения и преломления электромагнитных волн невидимого спектра подчиняются законам геометрической оптики видимого спектра.
Герц также померил скорость электромагнитной волны, создав стоячую волну и измерив её 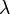 .
.
Электромагнитные волны регистрировались Герцем с помощью приемного вибратора, представляющего собой точно такое же устройство, что и излучающий вибратор. Под действием переменного электрического поля электромагнитной волны в приемном вибраторе возбуждаются колебания тока. Если собственная частота приемного вибратора совпадет с частотой электромагнитной волны, наблюдается резонанс и колебания в приемном вибраторе происходят с большой амплитудой. Герц обнаруживал их, наблюдая искорки в очень малом промежутке между проводниками приемного вибратора.
Своими опытами Герц доказал:
1)существование электромагнитных волн;
2)волны хорошо отражаются от проводников;
3)образование стоячих волн;
4)определил скорость волн в воздухе (она примерно равна скорости в вакууме - c).
Рассмотрим несколько понятий, касающихся опытов Герца:
1.Закрытый колебательный контур. Контур называется закрытым, так как он не излучает электромагнитные волны в пространство. Энергия, сообщаемая конденсатору, идет на нагревание проводов, а поэтому колебания затухающие (контур не излучает энергию в пространство).
2.Открытый колебательный контур.
| Открытый колебательный контур представляет из себя прямой кусок проводника (иногда один его конец заземляют). Открытый колебательный контур излучает энергию в виде электромагнитной волны и часть ее идет на нагревание контура. Открытый колебательный контур хорошо излучает волны, длина которых в 2 раза больше размеров контура (или в 4 раза больше, если контур заземлен). |
Кинематика прямолинейного движения
Материальная точка. Система отсчёта. Скорость и ускорение. Траектория, путь, перемещение. Уравнение траектории.
Кинематика – раздел механики, изучающий закономерности движения тел независимо от причин, вызывающих это движение
Материальная точка: Для описания движения тел в зависимости от условий конкретных задач в механике используются различные физические модели. Простейшей моделью является материальная точка. Материальная точка позволяет определять положение тела, независимо от размеров, формы и т.п. Тело можно считать материальной точкой только в тех случаях, когда его размеры, форма, вращение не имеют существенного значения в условиях решаемой задачи и ими можно пренебречь
Система отсчёта: Для определения положения движущегося тела в любой момент времени, вида движения, его скорости и т.п. необходимы три вещи: прибор для отсчета времени, тело отсчета и связанная с ним система координат. Система координат, тело отсчета и прибор для измерения времени образуют систему отсчета. Относительно системы отсчета и рассматривают движение тела. В декартовой системе координат положение точки в данный момент времени по отношению к этой системе характеризуется тремя координатами X,Y,Z или радиус вектором 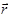 , проведенным из начала системы координат к точке. При этом проекции радиус-вектора на оси системы отсчета эквивалентны координатам материальной точки: X,Y,Z.
, проведенным из начала системы координат к точке. При этом проекции радиус-вектора на оси системы отсчета эквивалентны координатам материальной точки: X,Y,Z. 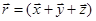 . В процессе движения МТ её координаты с течением времени изменяются. В общем случае её движение определяется скалярным ур-ниями: x=x(t); y=y(t); z=z(t) или
. В процессе движения МТ её координаты с течением времени изменяются. В общем случае её движение определяется скалярным ур-ниями: x=x(t); y=y(t); z=z(t) или 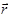 =
= 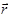 (t) – кинематические ур-ния движения материальной точки.
(t) – кинематические ур-ния движения материальной точки.
Траектория движения: Траектория движения материальной точки – линия описываемая этой точкой в пространстве. В зависимости от формы траектории поступательное движение может быть прямолинейным или криволинейным.
Уравнение траектории: Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат.
Движение точки в пространстве задается тремя уравнениями: x = f1(t); y = f2(t); z = f3(t);
Движение точки в плоскости (рис. 203) задается двумя уравнениями: x = f1(t); y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме.
Путь: Пройденный путь равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина. Длина участка траектории пройденного МТ с начала отсчета времени, называется длинной пути (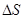 ) и является скалярной функцией времени
) и является скалярной функцией времени 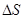 (t).
(t).
Перемещение: Направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение – векторная величина. Вектор 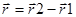 проведённый из начального положения движущейся точки в положение её в данный момент времени называется перемещением. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения
проведённый из начального положения движущейся точки в положение её в данный момент времени называется перемещением. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения  равен пройденному пути
равен пройденному пути 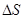 .
.
Скорость (V): Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки. Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени: 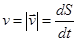 . Единица скорости – метр за секунду (м/с).
. Единица скорости – метр за секунду (м/с).
Ускорение (а): Скорость движения может изменяться как по модулю, так и по направлению. Быстрота изменения скорости характеризуется вектором ускорения  . Среднее ускорение – отношение изменения скорости
. Среднее ускорение – отношение изменения скорости 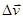 к промежутку времени
к промежутку времени 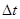 , в течении которого произошло это изменение.
, в течении которого произошло это изменение. 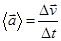 . Вектор среднего ускорения совпадает по направлению с вектором изменения скорости. Ускорение – векторная величина, равная первой производной скорости по времени. Единица ускорения – метр на секунду в квадрате (м/с2).
. Вектор среднего ускорения совпадает по направлению с вектором изменения скорости. Ускорение – векторная величина, равная первой производной скорости по времени. Единица ускорения – метр на секунду в квадрате (м/с2). 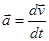
При использовании для описания движения декартовой системы координат положение материальной точки задаётся координатами X,Y,Z. При движении точки эти координаты изменяются во времени, и её движение описывается ур-ниями: x=x(t); y=y(t); z=z(t). В этом случае векторы скорости можно разложить на три взаимно перпендикулярные компоненты:  причём
причём 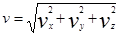 , а вектор ускорения (а) на
, а вектор ускорения (а) на 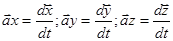 причём
причём 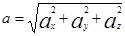
- Кинематика криволинейного движения МТ
Тангенциальное, нормальное и полное ускорение. Формулы расчёта тангенциального и нормального ускорения. Принцип относительности и суперпозиции движений.
Тангенциальное (касательное) ускорение 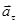 – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
– это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
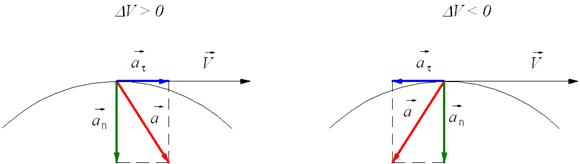
Направление вектора тангенциального ускорения 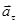 совпадает с направлением линейной скорости или противоположно ему.
совпадает с направлением линейной скорости или противоположно ему. 
Нормальное ускорение (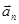 ) – характеризует изменение скорости по направлению и совпадает с нормалью траектории к центру её кривизны. Нормальное ускорение зависит от радиуса R окружности, по дуге которой тело движется в данный момент.
) – характеризует изменение скорости по направлению и совпадает с нормалью траектории к центру её кривизны. Нормальное ускорение зависит от радиуса R окружности, по дуге которой тело движется в данный момент. 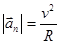 . Вектор
. Вектор 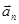 всегда направлен к центру окружности.
всегда направлен к центру окружности.
Полное ускорение, так как нормальное и тангенциальное ускорения взаимно перпендикулярны, полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой: 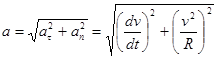
Направление полного ускорения также определяется правилом сложения векторов: 
Принцип относительности движения: Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчёта равноправны. Однако кинематические характеристики (траектория, перемещение, скорость) в разных системах оказываются различными. Величины, зависящие от выбора систем отсчёта, в которой производится их измерение, называют относительным.
Принцип суперпозиции движения: один из общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
- Кинематика вращательного движения твёрдого тела относительно неподвижной оси.
Угловое перемещение, угловая скорость и угловое ускорение. Связь между угловыми и линейными кинематическими величинами. Уравнение зависимости угла поворота от времени.
Угловое перемещение: Векторная величина, характеризующая изменение угловой координаты в процессе её движения. Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения 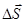 удобно рассматривать угловое перемещение
удобно рассматривать угловое перемещение 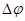 (угол поворота), измеряемое в радианах.
(угол поворота), измеряемое в радианах. 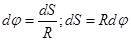
 Линейное перемещение конца радиус-вектора связанно с углом поворота
Линейное перемещение конца радиус-вектора связанно с углом поворота  соотношением
соотношением 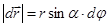 , в векторном виде
, в векторном виде 
При рассмотрении таких величин, как радиус-вектор, скорость, ускорение, вопрос в выборе их направления не возникает. Такие векторы называются полярными. Векторы типа 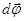 , направление которых связанно с направлением вращения называют аксиальными. Они не имеют точек приложения – их можно отложить от любой точки оси вращения.
, направление которых связанно с направлением вращения называют аксиальными. Они не имеют точек приложения – их можно отложить от любой точки оси вращения.
Угловая скорость (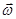 ): Если за промежуток времени
): Если за промежуток времени 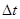 тело проворачивается на угол
тело проворачивается на угол 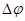 , быстрота его вращения характеризуется угловой скоростью.
, быстрота его вращения характеризуется угловой скоростью.  . Вектор
. Вектор 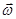 направлен вдоль оси вращения (как и вектор
направлен вдоль оси вращения (как и вектор 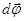 ), направление можно определить пользуясь правилом правого винта. Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора
), направление можно определить пользуясь правилом правого винта. Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора 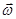 . Если
. Если 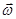 = const, то вращательное движение называют равномерным. Единица угловой скорости – радиан в секунду (рад/с).
= const, то вращательное движение называют равномерным. Единица угловой скорости – радиан в секунду (рад/с).
Время одного полного оборота тела вокруг оси называют периодом вращения T, а величину V, обратную периоду – частотой 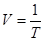 . За один период угол поворота радиус-вектора точки равен 2π рад.
. За один период угол поворота радиус-вектора точки равен 2π рад. 
Угловое ускорение: изменение вектора 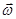 со временем характеризуют вектором углового ускорения
со временем характеризуют вектором углового ускорения  .
. 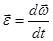 . Направление вектора
. Направление вектора  совпадает с направлением вектора
совпадает с направлением вектора  (приращение вектора
(приращение вектора 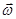 ). При ускоренном вращении
). При ускоренном вращении  совпадает с вектором
совпадает с вектором 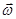 , при замедленном вращении
, при замедленном вращении  противоположно
противоположно 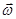 . Единица углового ускорения – радиан в секунду в квадрате (рад/с2).
. Единица углового ускорения – радиан в секунду в квадрате (рад/с2).
Связь между угловыми и линейными кинематическими величинами:
связь между линейной и угловой скоростью 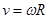 ; R – радиус окружности, по которой движется точка А,
; R – радиус окружности, по которой движется точка А, 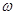 - угловая скорость точки А
- угловая скорость точки А
связь между тангенциальным и угловым ускорением (ось вращения неподвижна) 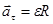
связь между нормальным (центростремительным) ускорением, угловой скоростью и линейной скоростью. 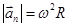
Модуль полного ускорения 
Уравнение зависимости угла поворота от времени:
При равномерном движении точки по окружности её траекторией является дуга. Точка движется с постоянной угловой скоростью 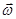 , а зависимость угла поворота точки от времени является линейной:
, а зависимость угла поворота точки от времени является линейной: 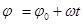 , где
, где 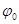 — начальное значение угла поворота.
— начальное значение угла поворота.
Эта же формула определяет угол поворота абсолютно твёрдого тела при его равномерном вращении вокруг неподвижной оси, то есть при вращении с постоянной угловой скоростью 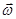 . Важной характеристикой данного типа движения является линейная скорость материальной точки
. Важной характеристикой данного типа движения является линейная скорость материальной точки 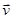 . Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения).
. Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения).
- Законы Ньютона.
Формулировка 1 закона Н. и принципы его действия. Причины изменения скорости тела. Инерциальные и неинерциальные системы отсчёта. Принцип относительности Галилея. Преобразования Галилея. Масса, сила, импульс тела. Формулировка второго закона Н. и уравнение движения материальной точки в инерциальной системе отсчёта. Третий закон Н. и принципы его действия. Инвариантность уравнения движения относительно преобразований Галилея.
Формулировка 1 закона Н. и принципы его действия: 1 закон Ньютона (закон Инерции): существуют системы отсчёта, в которых всякая материальная точка (тело)сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока при воздействии со стороны других тел это состояние не изменится. Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Если тело отсчета, входящее в систему отсчета покоится или совершает равномерное, прямолинейное движение, то на это тело не действуют никакие силы (1 з.Н.) или результирующая сил равна 0. Такая система может покоиться или двигаться только равномерно и прямолинейно (по инерции) и называется инерциальной.
Причины изменения скорости тела. Причиной изменения скорости тела является действие на него силы. Сила – векторная величина, которая является мерой механического воздействия на тело со стороны других тел или полей, в результате чего тело приобретает ускорение или деформируется.
Инерциальные и неинерциальные системы отсчёта. Инерциальная система отсчёта — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта. Неинерциальная система отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того, чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.
Принцип относительности Галилея. Принцип относительности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта. Различают принцип относительности Эйнштейна и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов механики.
Преобразования Галилея. Преобразования Галилея — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Преобразования Галилея подразумевают, одинаковость времени во всех системах отсчета и выполнение принципа относительности. Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, много меньше скорости света. Если ИСО S движется относительно ИСО S' с постоянной скоростью V вдоль оси X, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: x’=x+vt; y’=y; z’=z; t’=t или, используя векторные обозначения,  ; t’=t.
; t’=t.
Это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).
Масса, сила, импульс тела. Сила – векторная величина, которая является мерой механического воздействия на тело со стороны других тел или полей, в результате чего тело приобретает ускорение или деформируется. Единица силы – ньютон (Н). Ньютон – сила, которая сообщает ускорение 1 м/с2 телу массой 1 кг в направлении действия силы.
Масса – физическая величина определяющая инерционные (инертная масса) и гравитационные (гравитационная масса) свойства тела. В классической механике масса тела считается постоянной и равна массе покоя. Масса тела равна сумме масс всех частиц (материальных точек) из которых оно состоит. Массы взаимодействия тел обратно пропорциональны ускорениям, приобретаемыми телами в результате их взаимодействия.
Импульс тела — векторная физическая величина, являющаяся мерой механического движения тела. 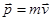 . Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
Формулировка второго закона Н. и уравнение движения материальной точки в инерциальной системе отсчёта. В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. 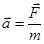 , а – ускорение тела, F – сила, приложенная к телу, m – масса материальной точки.
, а – ускорение тела, F – сила, приложенная к телу, m – масса материальной точки.  . Если на МТ одновременно действует несколько сил, то каждая из них действует независимо от других сил и сообщает точке ускорение, определяемое 2м з.Н. В инерциальных системах, ускорение, приобретаемое МТ, прямо пропорционально вызывающей его силе и совпадает с ней по направлению. И обратно пропорционально массе материальной точки. В инерциальных системах отсчёта производная импульса МТ по времени = действующей на неё силе. Скорость изменения импульса точки равна равнодействующей силе действующей на точку.
. Если на МТ одновременно действует несколько сил, то каждая из них действует независимо от других сил и сообщает точке ускорение, определяемое 2м з.Н. В инерциальных системах, ускорение, приобретаемое МТ, прямо пропорционально вызывающей его силе и совпадает с ней по направлению. И обратно пропорционально массе материальной точки. В инерциальных системах отсчёта производная импульса МТ по времени = действующей на неё силе. Скорость изменения импульса точки равна равнодействующей силе действующей на точку.  .F – результирующая всех сил, p – импульс MT.
.F – результирующая всех сил, p – импульс MT.
Если сила постоянна в течение конечного промежутка времени  , то закон изменения импульса принимает вид:
, то закон изменения импульса принимает вид: 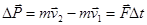 , v1 v2 – скорости тела во время t1 t2.
, v1 v2 – скорости тела во время t1 t2.
Третий закон Н. и принципы его действия. Тела действуют друг на друга с силами равными по модулю и противоположными по направлению. С какой силой тело 1 действует на тело 2, с такой же силой, но противоположной по направлению тело 2 действует на тело 1 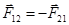 . Третий закон Ньютона справедлив независимо от того, покоятся взаимодействующие тела или находятся в движении, находятся они в контакте друг с другом или разделены пространством.
. Третий закон Ньютона справедлив независимо от того, покоятся взаимодействующие тела или находятся в движении, находятся они в контакте друг с другом или разделены пространством.
Инвариантность уравнения движения относительно преобразований Галилея. Инвариантность уравнений движения относительно преобразований Галилея представляет собой математическую формулировку принципа относительности классической механики: законы движения одинаковы во всех системах координат, равномерно движущихся относительно друг друга. Первый постулат теории относительности согласуется с этим принципом и обобщает его на законы распространения света. Однако одновременное применение обоих постулатов находится в противоречии с преобразованиями Галилея. Если ИСО S движется относительно ИСО S' с постоянной скоростью V вдоль оси X, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: x’=x+vt; y’=y; z’=z; t’=t или, используя векторные обозначения,  ; t’=t.
; t’=t.
- Силы в механике.
Классификация сил природы. Закон всемирного тяготения. Физический смысл гравитационной постоянной. Сила тяжести и веса тела. Упругие силы, закон Гука. Силы трения и сопротивления. Сложение сил.
Классификация сил природы. Сила количественная мера изменения скорости тела. Силы могут иметь различную физическую природу (сила трения, сила тяжести, сила упругости…). Сила является векторной величиной. Векторная сумма всех сил действующих на тело называется равнодействующей силой. Эталонная сила в системе СИ называется – Ньютон(Н). Все силы в природе делятся на фундаментальные силы (сила всемирного тяготения, сила электромагнитного взаимодействия и т.д.) и нефундаментальные (сила Архимеда, сила упругости, сила трения и тд.).
Закон всемирного тяготения. Сила тяготения (гравитационная сила) – силы притяжения, которые подчиняются закону всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними: 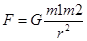 Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной G = 6,67·10–11 Н·м2/кг2 (СИ).
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной G = 6,67·10–11 Н·м2/кг2 (СИ).
Сила тяжести и вес тела. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R З – ее радиус, m – масса данного тела, то сила тяжести равна 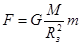 ,
, 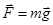
где g – ускорение свободного падения у поверхности Земли:  . Под действием силы притяжения к земле все тела падают в данном месте с одинаковым ускорением (g), которое называется ускорением свободного падения. Тогда на основании 2 з.Н. что это ускорение вызывается силой тяжести.
. Под действием силы притяжения к земле все тела падают в данном месте с одинаковым ускорением (g), которое называется ускорением свободного падения. Тогда на основании 2 з.Н. что это ускорение вызывается силой тяжести. 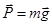 . Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2.
. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2.
Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Сила тяжести равна весу, когда ускорение тела относительно земли = 0, т.е. когда тело неподвижно относительно земли или движется с постоянной скоростью. Если имеет место ускорение, то  . Вес тела может быть больше или меньше силы тяжести: если g и a направлены в одну сторону (тело движется вниз или падает), то G < mg, и если наоборот, то G < mg. Если же тело движется с ускорением a = g, то G = 0 – т.е. наступает состояние невесомости.
. Вес тела может быть больше или меньше силы тяжести: если g и a направлены в одну сторону (тело движется вниз или падает), то G < mg, и если наоборот, то G < mg. Если же тело движется с ускорением a = g, то G = 0 – т.е. наступает состояние невесомости.
Упругие силы, закон Гука. Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости. При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются.
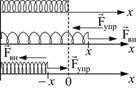 Рассмотрим упругие деформации. В деформированном теле возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы – Fвн пружина получает удлинение x, в результате в ней возникает упругая сила – Fупр, уравновешивающая Fвн. Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости Fупр.
Рассмотрим упругие деформации. В деформированном теле возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы – Fвн пружина получает удлинение x, в результате в ней возникает упругая сила – Fупр, уравновешивающая Fвн. Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости Fупр.
Закон Гука -Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации. 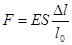 ; E- модуль Юнга (характеризует упругие св-ва матер.), S – площадь поперечного сечения,
; E- модуль Юнга (характеризует упругие св-ва матер.), S – площадь поперечного сечения, 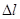 - абсолютное удлинение,
- абсолютное удлинение, 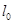 - длина в недеформированном состоянии. В виде уравнения закон Гука записывается в следующей форме: F = –kx, где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействует деформации: при растяжении стремится укоротиться, а при сжатии — распрямиться. Зкон Гука действует только при относительно небольших сжатиях или растяжениях. Пока вещество сохраняет свои упругие свойства, силы деформации прямо пропорциональны ее величине, и вы имеете дело с линейной системой — каждому равному приращению приложенной силы соответствует равное приращение деформации. Стоит перетянуть резину за предел эластичности, и межатомные связи-пружины внутри вещества сначала ослабевают, а затем рвутся — и простое линейное уравнение Гука перестает описывать происходящее. В таком случае принято говорить, что система стала нелинейной.
- длина в недеформированном состоянии. В виде уравнения закон Гука записывается в следующей форме: F = –kx, где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействует деформации: при растяжении стремится укоротиться, а при сжатии — распрямиться. Зкон Гука действует только при относительно небольших сжатиях или растяжениях. Пока вещество сохраняет свои упругие свойства, силы деформации прямо пропорциональны ее величине, и вы имеете дело с линейной системой — каждому равному приращению приложенной силы соответствует равное приращение деформации. Стоит перетянуть резину за предел эластичности, и межатомные связи-пружины внутри вещества сначала ослабевают, а затем рвутся — и простое линейное уравнение Гука перестает описывать происходящее. В таком случае принято говорить, что система стала нелинейной.
Силы трения и сопротивления. Силой трения называют силу, которая возникает при соприкосновении двух тел и препятствует их относительному перемещению. Трение является одним из проявлений контактного взаимодействия сил. Трение бывает двух видов: внутреннее и внешнее. Силы внешнего трения возникают на поверхности контакта двух тел. Они приложены к телам в соответствии с третьим законом Ньютона и направленны по касательной к поверхности контакта. Внутреннее трение – тангенциальное взаимодействие между слоями одного и того же тела.
Трение тв. Тел без смазки – сухое трение. Существует 3 вида сухого трения: трение покоя, трение скольжения, трение качения.
Трение покоя. Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону. Сила трения покоя не может превышать некоторого максимального значения (F тр) max. Если внешняя сила больше (F тр)max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения и зависит от относительной скорости тел. Однако, во многих случаях приближенно силу трения скольжения можно считать независящей от величины относительной скорости тел и равной максимальной силе трения покоя. Эта модель силы сухого трения применяется при решении многих простых физических задач. Сила трения скольжения пропорциональна силе нормального давления тела на опору, а следовательно, и силе реакции опоры 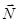 .
.  . – закон Кулона (Амонтона). Коэффициент пропорциональности μ называют коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости.
. – закон Кулона (Амонтона). Коэффициент пропорциональности μ называют коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости.  . Коэффициент трения равен
. Коэффициент трения равен 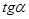 , при котором начинается скольжение тела по наклонной плоскости.
, при котором начинается скольжение тела по наклонной плоскости.
Трение качения. Сопротивление движению, возникающее при перекатывании тел друг по другу т.е. сопротивление качению одного тела (катка) по поверхности другого.  .
. 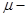 коэффициент трения качения, имеющий размерность длины, N – прижимающая сила, R – радиус катящегося тела.
коэффициент трения качения, имеющий размерность длины, N – прижимающая сила, R – радиус катящегося тела.
Жидкое трение. Сила трения, которая ввозникает при движении твёрдого тела в жидкости или газе. Отсутствует сила трения покоя. Если тело покоится относительно жидкости или газа, то на него действует сила перпендикулярная к поверхности соприкосновения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела.Сила вязкого трения сильно зависит от скорости тела. При достаточно малых скоростях 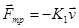 , при больших скоростях
, при больших скоростях 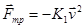 . Сила направленна противоположно скорости. Коэффициенты пропорциональности (К) в этих соотношениях зависят от формы тела.
. Сила направленна противоположно скорости. Коэффициенты пропорциональности (К) в этих соотношениях зависят от формы тела.
Сложение сил. При одновременном действии на одно тело нескольких тел тело движется с ускорением, являющимся векторной суммой ускорений, которые возникли бы под действием каждого тела в отдельности. Действующие на тело силы, приложенные к одной точке тела, складываются по правилу сложения векторов. Векторная сумма всех одновременно действующих на тело сил называется равнодействующей.
- Неинерциальные системы отсчёта.
Неинерциальные системы отсчёта, привести примеры. Сила инерции, сила Кориолиса. Уравнение движения в неинерциальных системах отсчёта. Принцип эквивалентности. Границы применимости Ньютоновской механики.
Неинерциальные системы отсчёта, привести примеры. Система отсчета, в которой наблюдается ускорение движения тел, при отсутствии действия на них сил других тел. Неинерциальная система – система отсчёта, которая ускоряется, замедляется или вращается относительно инерциальной. Например: Карусель, которая вращается относительно стоящего за её приделами человека, является неинерциальной системой отсчёта.
Сила инерции, сила Кориолиса. Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета: 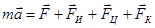 , где
, где
 - сила, действующая на тело со стороны других тел;
- сила, действующая на тело со стороны других тел;
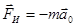 - сила инерции, действующая на тело относительно поступательно движущейся НСО.
- сила инерции, действующая на тело относительно поступательно движущейся НСО. 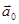 - ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
- ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
 — центробежная сила инерции, действующая на тело относительно вращающейся НСО.
— центробежная сила инерции, действующая на тело относительно вращающейся НСО. 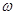 - угловая скорость НСО относительно ИСО,
- угловая скорость НСО относительно ИСО, 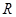 - расстояние от тела до центра вращения;
- расстояние от тела до центра вращения;
 — кориолисова сила инерции, действующая на тело, движущееся со скоростью
— кориолисова сила инерции, действующая на тело, движущееся со скоростью 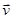 относительно вращающейся НСО.
относительно вращающейся НСО. 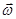 - угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
- угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
Сила Кориолиса, действующая на материальную точку в неинерциальной системе отчёта, вызывает ускорение точки, равное ускорению Кориолиса, взятому со знаком минус.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Сила Кориолиса определяет направление вращения вихрей циклонов, которые мы наблюдаем на снимках, полученных с метеоспутников. Изначально воздушные массы начинают прямолинейно устремляться из областей высокого атмосферного давления в области пониженного атмосферного давления, однако сила Кориолиса заставляет их закручиваться по спирали. (С тем же успехом можно утверждать, что воздушные потоки продолжают двигаться прямолинейно, но, поскольку Земля под ними поворачивается, нам, находящимся на поверхности планеты, кажется, что они движутся по спирали.). В Северном и Южном полушариях сила Кориолиса действует на движущееся тело в прямо противоположных направлениях. Именно поэтому в Северном полушарии вихри циклонов кажутся закрученными против часовой стрелки, а в Южном — по часовой стрелке.
Уравнение движения в неинерциальных системах отсчёта. При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной. Основное уравнение динамики относительного движения материальной точки имеет вид: 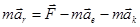 где m - масса тела,
где m - масса тела, 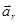 -ускорение тела относительно неинерциальной системы отсчёта,
-ускорение тела относительно неинерциальной системы отсчёта,  - сумма всех внешних сил, действующих на тело,
- сумма всех внешних сил, действующих на тело, 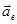 - переносное ускорение тела,
- переносное ускорение тела, 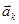 - кориолисово ускорение тела.
- кориолисово ускорение тела.
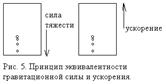 Принцип эквивалентности. Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное достаточно малое тело — гравитационная или сила инерции Однородное гравитационное поле эквивалентно постоянному ускорению.
Принцип эквивалентности. Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное достаточно малое тело — гравитационная или сила инерции Однородное гравитационное поле эквивалентно постоянному ускорению.
Поиск по сайту: