Кинетическая и потенциальная энергия

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.

Механическая энергия. Закон сохранения полной механической энергии: Есть разные формы энергии, и они могут превращаться одна в другую. Если из двух видов энергии один уменьшается ровно на столько, на сколько увеличивается другой, то это значит, что сумма энергий обоих видов остается неизменной. . Сумма кинетической и потенциальной энергии системы называется полной механической энергией. Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

1. Момент силы. Момент импульса частицы.

Момент силы. Момент импульса. Пара сил. Момент пары сил. Изменение момента импульса. Закон сохранения момента импульса.

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. , в системе СИ –Н*м. При применении момента силы речь идет о статике, о неподвижных системах, в которых нет ни вращательного, ни орбитального движения, и потому модуль радиус-вектора r является обычным расстоянием с размерностью L и единицей метр. Момент Силы характеризует способность силы вращать тело.

Момент импульса. Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. , единица изменения в системе СИ - м²·кг·с⁻¹. r — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p (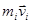) — импульс частицы. Момент импульса направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы и и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от к 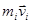происходит против часовой стрелки). Векторную сумму моментов импульсов всех материальных точек системы называют моментом импульса (количества движения) системы относительно точки О.

Пара сил. Момент пары сил. Парой сил называется приложенная к твердому телу система двух сил (), равных по модулю, параллельных и направленных в противоположные стороны: .

Расстояние d между линиями действия сил пары называется плечом пары; плоскость , в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар.

Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары характеризуется векторной величиной, называемой моментом пары. Момент пары сил относительно точки O

не зависит от выбора точки O и равен моменту одной из сил пары относительно точки приложения другой силы: . Момент пары сил M перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары: . Векторный момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором. Две пары сил, имеющие одинаковые векторные моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.

Изменение момента импульса. Для изменения момента вращения необходим момент силы — то есть, сила, приложенная по направлению, отличному от направления оси вращения, и на некотором удалении от нее.

Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке, и состоит в следующем: если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется. Если M = 0, то , откуда 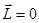. Другими словами, момент импульса замкнутой системы с течением времени не изменяется. Из основного закона динамики тела вращающегося вокруг неподвижной оси z (), следует закон сохранения момента импульса тела относительно оси. Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью.

1. Уравнение динамики вращательного движения твёрдого тела. Кинетическая энергия вращающегося тела.

Момент импульса тела относительно оси. Момент инерции тела относительно оси. Теорема Штейнера. Уравнение динамики твёрдого тела, вращающегося вокруг неподвижной оси. Кинетическая энергия вращающегося тела. Работа внешних сил при вращении твердого тела.

Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если 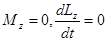, откуда .

Момент инерции тела относительно оси вращения z – это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси: .

Теорема Штейнера. Теорема Штейнера сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс.Момент инерции тела J_z относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс (С) тела, сложенному с произведением массы m тела на квадрат расстояния, а между осями: .

Уравнение динамики твёрдого тела, вращающегося вокруг неподвижной оси. Суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение: . Учитывая, что момент импульса твердого тела , уравнение динамики твердого тела можно представить в виде .

Кинетическая энергия вращающегося тела. При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:

то есть кинетическая энергия вращающегося тела равна той работе, которую может совершить это тело до полной остановки.

Поиск по сайту: