 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача о разорении в математической постановке
Для ее решения вводятся следующие характеристики:
1. Скорость получения страховки (U (t)
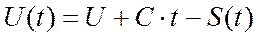 (50)
(50)
где U – начальные активы;
S(t) – суммарные страховые выплаты;
t- текущее время;
С- фиксированная скорость
2. Вероятность окончательного разорения (φ(u))
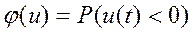 (51)
(51)
где – P- вероятность.
3.Верхняя граница этой вероятности задается неравенством Лундсберга
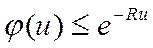 (52)
(52)
где – R-коэффициент Лундсберга.
23.Задача о перестраховании, при которой используются три подхода;
1. пропорциональное перестрахование;
2.эксценотное перестрахование;
3.перестрахование с учетом разорения.
ММ, и формулы их описывающие выглядят так:
Y=αX (53)
H=(1-α)X(54)
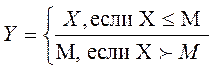 (55)
(55)
 (56)
(56)
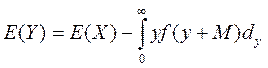 (57)
(57)
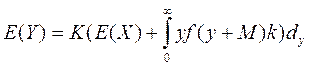 (58)
(58)
где Y –сумма, выплачиваемая страховщиком;
Х- размер требование;
Н - сумма, выплачиваемая перестраховщиком;
М -сумма (уровень) удержания –безусловная франшиза – льгота, условия страхового договора, предусматривающее освобождение страховщика от возмещения убытков, не превышающих определенного размера;
К - некоторый множитель
Поиск по сайту: