Проверить наличие мультиколлинеарности в модели. Сделать вывод

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. В результате высококоррелированные объясняющие переменные действуют в одном направлении и имеют недостаточно независимое колебание, чтобы дать возможность модели изолировать влияние каждой переменной. Проблема мультиколлинеарности возникает только в случае множественной регрессии. Мультиколлинеарность особенно часто имеет место при анализе макроэкономических данных (например, доходы, производство). Получаемые оценки оказываются нестабильными как в отношении статистической значимости, так и по величине и знаку (например, коэффициенты корреляции). Следовательно, они ненадежны. Значения коэффициентов R² могут быть высокими, но стандартные ошибки тоже высоки, и отсюда t- критерии малы, отражая недостаток значимости.

Для проверки появления мультиколлинеарности применяются два метода, доступные во всех статистических пакетах[3][3]:

Ø Ø Вычисление матрицы коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными очень велики, то, следовательно, они коллинеарны. Однако, при этом не существует единого правила, в соответствии с которым есть некоторое пороговое значение коэффициента корреляции, после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии.

Ø Ø Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:

ü ü 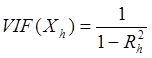, где - значение коэффициента множественной корреляции, полученное для регрессора 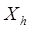как зависимой переменной и остальных переменных 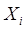. При этом степень мультиколлинеарности, представляемая в регрессии переменной 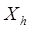, когда переменные включены в регрессию, есть функция множественной корреляции между 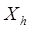и другими переменными .

ü ü Если , то объясняющие переменные, коррелирующие между собой, считаются мультиколлинеарными.

Существует еще ряд способов, позволяющих обнаружить эффект мультиколлинеарности:

Ø Ø Стандартная ошибка регрессионных коэффициентов близка к нулю.

Ø Ø Мощность коэффициента регрессии отличается от ожидаемого значения.

Ø Ø Знаки коэффициентов регрессии противоположны ожидаемым.

Ø Ø Добавление или удаление наблюдений из модели сильно изменяют значения оценок.

Ø Ø Значение F-критерия существенно, а t-критерия – нет.

Для устранения мультиколлинеарности может быть принято несколько мер:

Ø Ø Увеличивают объем выборки по принципу, что больше дан­ных означает меньшие дисперсии оценок МНК. Проблема реализации этого варианта решения состоит в трудности на­хождения дополнительных данных.

Ø Ø Исключают те переменные, которые высококоррелированны с остальными. Проблема здесь заключается в том, что воз­можно переменные были включены на теоретической основе, и будет неправомочным их исключение только лишь для то­го, чтобы сделать статистические результаты «лучше».

Ø Ø Объединяют данные кросс-секций и временных рядов. При этом методе берут коэффициент из, скажем, кросс-секционной регрессии и заменяют его на коэффициент из эквивалентных данных временного ряда.

Проделанные манипуляции позволяют предположить, что мультиколлинеарность может присутствовать (оценки любой регрессии будут страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными), однако в данном примере это не влияет на результаты оценки регрессии. Следовательно, выделять «лишние» переменные не стоит, так как это отражается на содержательном смысле модели.

Поиск по сайту: