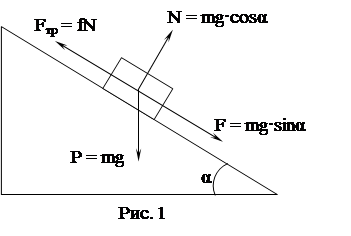
Введение. Рассмотрим тело, находящееся на наклонной плоскости (рис.1)

Рассмотрим тело, находящееся на наклонной плоскости (рис.1).

Движение тела в поле силы подчиняется второму закону Ньютона

где а – ускорение тела, F – сила действующая на тело и m – масса. В случае постоянства действующей силы и неизменности массы ускорение тела является постоянной величиной. Зная, что

получим уравнения:

(1)

где S₀ – начальная координата, V₀ – начальная скорость. Не трудно видеть, что V(t) представляет собой прямую, а S(t) параболу. В случае равенства нулю начальной скорости и координаты уравнения (1) примут вид:

(2)

Определяя экспериментально зависимость S(t), можно определить V(t) путем однократного численного дифференцирования, а ускорение двукратным дифференцированием.

Сила трения – сила, которая препятствует скольжению соприкасающихся тел относительно друг друга. Различают внешнее (сухое) трение, которое возникает в плоскости касания тел при их относительном перемещении и внутреннее (жидкое или вязкое) трение, которое возникает между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. При сухом трении, если тела неподвижны относительно друг друга, то говорят о трении покоя, если же происходит относительное перемещение тел, то в зависимости от характера движения говорят о трении скольжения, качения или верчения. В случае, когда скользящие тела разделены прослойкой жидкости (смазки), трение происходит в слое смазки. При этом говорят о гидродинамическом трении.

Движение тела начнется, только тогда, когда тангенциальная составляющая F = mg∙sinα силы тяжести Р = mg окажется больше силы трения F_TP = fN (N = mg∙cosα – реакция опоры). В предельном случае (начало скольжения) F = F_TP, или Рsinα₀ = f_пPcosα₀, откуда

f_п = tgα₀ - коэффициент трения покоя. (3)

Для определения коэффициента трения скольжения воспользуемся вторым законом Ньютона применительно к рассматриваемой задаче:

mа = mgsinα - fmgcosα.

Из полученного выражения выразим коэффициент трения скольжения f

(4)

Закон сохранения энергии – один из фундаментальных законов природы, результат обобщения многих экспериментальных данных. Идея закона принадлежит М.В.Ломоносову, а количественная формулировка дана Ю.Майером и Г.Гельмгольцем. В случае отсутствия внешних неконсервативных сил закон сохранения механической энергии можно представить в виде: Т + П = Е = const, т.е. полная механическая энергия системы остается постоянной.

Рассмотрим процесс скатывания тела вращения по наклонной плоскости под действием силы тяжести. При качении тела без проскальзывания (т.е. в отсутствии рассеяния механической энергии) происходит превращение потенциальной энергии П = mgh в кинетическую энергию поступательного и вращательного движения тела. Здесь m, V, J, ω – масса, скорость центра тяжести, момент инерции относительно центра тяжести, угловая скорость. Закон сохранения энергии запишется в виде:

(5)

С учетом того, что уравнение (1) перепишем в виде

выражая отсюда скорость поступательного движения, получим

где – коэффициент, определяющий долю кинетической энергии потерянной на вращение при переходе потенциальной энергии в кинетическую. Подставив выражения для момента инерции шара и диска в коэффициент легко убедиться, что для шара ξ = 0,40 и для диска ξ = 0,5.

Если угол установки направляющей известен и равен α, то при длине участка S_i максимально возможная скорость скатывания тела будет равна (то есть, равна скорости свободно падающего тела). Здесь h_i=S_isinα.

Определяя при скатывании различных тел V_i на разных участках пути S_i при фиксированном угле наклона α, можно определить значение потерь энергии на вращение и сравнить их с теоретическими, сопоставляя V_{mах i} и V_i.

Поиск по сайту: