Применение теории вычетов

Вычеты

В случае, когда комплекснозначная функция регулярна в области, интеграл от нее по границе области равен нулю согласно интегральной теореме Коши. Возникает вопрос: чему равен интеграл по границе области в случае, когда внутри области содержится конечное число особых точек однозначного характера интегрируемой функции? Итак, предположим, что функция регулярна в области D, за исключением конечного числа особых точек однозначного характера. Пусть замкнутая кривая C лежит в области D и ограничивает область , внутри которой содержатся особых точек . Вырежем из области попарно непересекающиеся окрестности особых точек, ограниченных замкнутыми кривыми . Мы получим новую – (n +1)-связную (то есть имеющую n дырок) область .

В области функция регулярна, поэтому согласно интегральной теореме Коши , где все замкнутые контуры обходятся против часовой стрелки. Следовательно, справедлива формула: . Таким образом, если в области функция имеет конечное число особенностей однозначного характера, интеграл по границе области равен сумме интегралов по замкнутым кривым, окружающим каждую особую точку. Такой интеграл по замкнутой кривой, окружающей одну особую точку однозначного характера и проходимой против часовой стрелки, деленный на 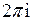, называется вычетом функции в точке и обозначается 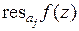. То есть, 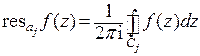. С учетом введенного обозначения справедлива теорема о вычетах:

.

Мы знаем, что в кольце, расположенном в окрестности особой точки однозначного характера регулярная функция раскладывается в ряд Лорана. Следовательно, если разложение функции в окрестности особой точки имеет вид , то согласно правилу интегрирования степеней получим . Таким образом, . То есть, вычет функции в особой точке однозначного характера равен коэффициенту при степени (-1) разложения функции в ряд Лорана в окрестности этой особой точки.

Таким образом, интегрирование функций по замкнутым контурам сводится к вычислению коэффициентов при степени (-1) разложения функции в ряд Лорана в окрестности всех особых точек однозначного характера, расположенных в области, ограниченной заданным контуром и .

Вычисление вычета функции f(z) в точке a с помощью MAXIMA возможно при применении команды residue(f(z),z,a).

П р и м е р ы. 1. Для того, чтобы вычислить вычет функции в особой точке , введем команду residue((8*z^3-z^2+3*z)*(z^2+4)^(-3),z,2*%i) и нажмемShift+Enter. Ответом будет .

2. Вычислить , где C – а) окружность радиуса 1 с центром в точке 0, б) граница полукруга радиуса 3, основанием которого является отрезок [-3,3], расположенного в верхней полуплоскости, в) граница полукруга радиуса 3, основанием которого является отрезок [-3,3], расположенного в нижней полуплоскости, г) окружность радиуса 4 с центром в точке 0. Все контуры проходятся против часовой стрелки.

а) Для функции особыми точками являются точки 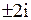, в круге радиуса 1 с центром в 0 особых точек нет. Значит согласно интегральной теореме Коши =0.

б) Для функции , заданной в верхнем полукруге радиуса 3 с центром 0, особой точкой является точка 2i. Следовательно, .

в) Для функции , заданной в нижнем полукруге радиуса 3 с центром 0, особой точкой является точка -2i. Следовательно, .

г) Для функции , заданной в круге радиуса 4 с центром в точке 0, обе особые точки однозначного характера 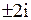находятся в этом круге. Следовательно, согласно теореме о вычетах

Применение теории вычетов

Теорему о вычетах удобно применять для вычисления не только интегралов по замкнутому контуру от комплекснозначных функций, но и собственных и несобственных интегралов от функций вещественного переменного.

1. Вычисление интегралов от -периодической функции вида , где означает рациональную дробь по каждому из переменных. Такие интегралы сводятся к вычислению контурных интегралов по единичной окружности с помощью представлений и замены переменной интегрирования: . Если исходная переменная интегрирования проходит, возрастая, отрезок , комплексная переменная проходит единичную окружность против часовой стрелки. При этом . Поэтому 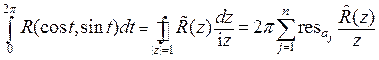. Здесь суммируются вычеты во всех особых точках функции , попавших внутрь единичного круга.

П р и м е р. Вычислить .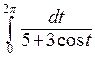

После введения переменного получим

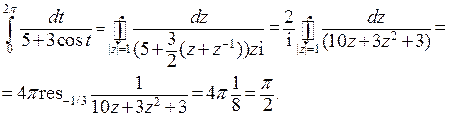
Заметим, что у функции особой точкой является не только

-1/3, но и -3. Вторая особая точка расположена вне единичного круга, поэтому вычет в этой точке не вычислялся.

2. Вычисление несобственных интегралов вида , где – рациональная дробь и для сходимости несобственного интеграла 1-го родя необходимым условием является требование: .

Мы знаем, что 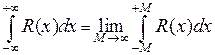. Введем интеграл по замкнутому контуру С, ограничивающему полукруг радиуса M с центром 0, расположенный в верхней полуплоскости.

Этот контур состоит из отрезка [- M,M ] и дуги . То есть . На отрезке [- M,M ] комплексное переменное z превращается в вещественное переменное x. На полуокружности введем новое переменное интегрирование: , где . Тогда . Согласно условию сходимости несобственного интеграла 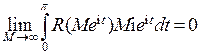. Поэтому 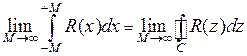. Согласно теореме о вычетах для вычисления интеграла по контуру C следует сложить вычеты во всех особых точках, расположенных внутри соответствующего полукруга. Но так как с ростом числа M полукруг превращается в полуплоскость,

, где , – особые точки функции R(z), расположенные в верхней полуплоскости.

П р и м е р. Вычислить .

Найдем особые точки подынтегральной функции с помощью MAXIMA. Запишем solve(x^4+10*x^2+9=0,x) и нажмемShift+Enter. Мы получим 4 особые точки – нули знаменателя подынтегральной функции: -i, i, -3i, 3i. Только 2 из них расположены в верхней полуплоскости: i и 3i. Поэтому .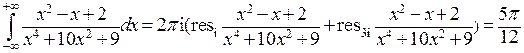

Поиск по сайту: