Геометрическое изображение функции двух переменных

Функция у = f(x) одной переменной допускает наглядное изображение в виде некоторой линии - графика функции на плоскости Оху. Аналогично, функцию двух переменных z = f(x, y) можно наглядно представить с помощью некоторой поверхности. Рассмотрим пространственную прямоугольную систему координат Охуz и функцию z = f(x, y) = f(P), определенную на некотором множестве D точек плоскости Оху. Каждой точке P(x,y) из множества D соответствует некоторое число z = f(Р).

Проведем в точке Р перпендикуляр к плоскости Оху и на нем отложим отрезок РМ, длина которого равна | f(P) |, при этом точку М возьмем над плоскостью Оху, если f(Р) > 0, и под плоскостью Оху, если f(Р) < 0. Таким образом, точка М имеет координаты (x, y, z), где х и у − координаты точки Р, а z − значение функции в этой точке, т.е. z = f(P). Такое построение проделаем для каждой точки Р из области определения функции z = f(x, y). Множество точек пространства, координаты которых связаны соотношением z = f(x, y), образуют некоторую поверхность, которая называется графиком данной функции и является ее геометрическим изображением.

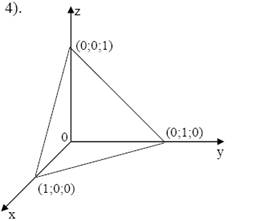
Пример 6. Графиком функции

z = 1 - x - y

является плоскость, проходящая через точки (1; 0; 0;), (0; 1; 0) и (0; 0; 1) на рис. 3.

Рис. 3

Определение 3. Линией уровня функции z = f(x, y) называется множество точек плоскости Оху, в которых функция принимает одно и то же значение.

Эту линию можно получить пересе­че­нием графика функции z = f(x, y) плос­костью z = с (с - константа) и проектиро­ванием линии пересечения на плоскость Оху (рис. 5). Рис. 5

Поиск по сайту: