Ошибки, возможные в определении

Определение должно быть соразмерным т. е. объем опре­деляющего понятия должен быть равен объему определяемого понятия. Dfd=Dfn. Это правило часто нарушается, в результате чего возникают логические ошибки в определении. Типы этих логических ошибок:

а) широкое определение; когда Dfd<Dfn. Такая ошибка содер­жится в следующих определениях: «Лошадь — млекопитающее и позвоночное животное» (Здесь понятие «лошадь» нельзя от­личить от понятий «корова» или «коза».);

б) узкое определение, когда Dfd>Dfn. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?);

в) определение в одном отношении широкое, в другом — уз­кое. В этих неправильных определениях Dfd>Dfn и Dfd<Dfn (в
разных отношениях). Например, «Бочка — сосуд для хранения
жидкостей». С одной стороны, это широкое определение, так как
сосудом для хранения жидкостей может быть и чайник, ведро и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей.

Приемы, сходные с определением понятий:

– Описание состоит в перечислении внешних черт предмета с це­лью нестрогого отличения его от сходных с ним предметов. Описание дает чувственно-наглядный образ предмета, который человек может составить с помощью творческого или воспроиз­водящего представления. Описание включает как существенные, так и несущественные признаки;

– Характеристика дает перечисление лишь некоторых внутрен­них, существенных свойств человека, явления, предмета, а не его внешнего вида, как это делается с помощью описания;

– Сравнение, при помощи которого один предмет сопоставляется с другим, сходным в каком-либо отношении.К сравнению прибегают как на уровне научного познания, так и на уровне художественного отображения действительности.

Классификационные операции с понятиями. При изучении какого-либо понятия нередко встает задача раскрыть его объем, т.е. распределить предметы, которые мыслятся в понятии на отдельные группы.

1. Деление — это логическая операция, посредством которой объём делимого понятия (множество) распределяется на ряд подмножеств с помощью избранного основания деления. Напри­мер, органы чувств делят на органы зрения, слуха, обоняния, осязания и вкуса. Если с по­мощью определения понятия раскрывается его содержание, то с помощью деления понятия раскрывается его объем.

Признак, по которому производится деление объема понятия, называется основанием деления. Подмножества, на которые раз­делен объем понятия, называются членами деления. Делимое понятие — это родовое, а его члены деления — это виды данного рода, соподчиненные между собой, т. е. не пересекающиеся по своему объему

Объем понятия можно делить по различным основаниям в зависимости от цели деления, от практических задач. Но при каждом делении на некотором его уровне должно браться лишь одно основание. Так, например, мышцы в зависимости от места их расположения делят на мышцы головы, шеи, туловища, мышцы верхних конечностей и мышцы нижних конечностей. Мышцы делят по их форме и функции. В зависимости от формы мышцы делят на широкие, длинные, короткие, круговые. По функции различают мышцы — сгибатели, разгибатели, приводя­щие и отводящие мышцы, а также мышцы, вращающие внутрь и наружу.

Правила деления понятий:

– Соразмерность деления: объем делимого понятия должен быть равен сумме объемов членов деления, Например, высшие растения делятся на травы, кустарники и деревья;

– Деление должно проводиться только по одному основанию. Это означает, что нельзя брать два или большее число призна­ков, по которым бы производилось деление. Если будет нарушено это правило, то произойдет перекрещи­вание объемов понятий, которые появились в результате деления. Неправильным является такое деление: «Транспорт делится на наземный, водный, воздушный, транспорт общего пользования, транспорт личного пользования», — ибо допущена ошибка «подмена основания», т. е. деление произведено не по одному основанию;

– Члены деления должны исключать друг друга, т. е. не иметь общих элементов, быть соподчиненными понятиями, объемы которых не пересекаются. Нельзя, к примеру, разбивать все целые числа на такие классы: числа, кратные двум; числа, кратным трем; числа, кратные пяти и т.д. Эти классы пересекаются, и, допустим, число 10 попадает и в первый и в третий классы, а число 6 — и в первой и во второй классы;

– Деление должно быть непрерывным, т. е. нельзя делать скачки в делении. Будет допущена ошибка, если мы скажем: «Сказуемые делятся на простые, на составные глагольные; и составные именные». Правильным будет сначала разделить сказуемые на простые и составные, а затем уже составные сказуемые разделить на составные глагольные и составные именные.

Виды деления:

– по видообразующему признаку – основа­нием деления является тот признак, по которому образуются видовые понятия. На­пример, по величине углы делятся на прямые, острые, тупые;

– дихотомическое (двучленное) деление – объем делимого понятия делится на два противоречащих понятия: А и не-А. Примеры: «Организмы делятся на одноклеточные и многокле­точные (т. е. неодноклеточные)»; «Вещества делятся на органи­ческие и неорганические».

2.Классификация является разновидностью деления понятия, представляет собой вид последовательного деления и образует развернутую систему, в которой каждый ее член (вид) делится на подвиды и т. д. От обычного деления классификация отличается относительно устойчивым характером.

Для классификации обязательно выполнение всех правил, сформулированных относительно операции деления понятий.

Существует классификация по видообразующему признаку и дихотомическая.

Очень важен выбор основания классификации. Разные основа­ния дают различные классификации одного и того же понятия.

Классификация может производиться по существенным при­знакам (естественная) и по несущественным признакам (вспомо­гательная).

Каждая классификация относительна, приблизительна, она в огрубленной форме раскрывает связи между классифициру­емыми предметами. Существуют переходные формы, которые трудно отнести к той или иной определенной группе.

Обобщение и ограничение.

Обобщить понятие — значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Например, обобщая понятие «Минис­терство юстиции Российской Федерации», мы переходим к понятию «министерство юстиции». Продолжая операцию обобщения, можно последовательно обра­зовывать понятия «министерство», «орган государственного управ­ления». Каждое последующее понятие является родом по отноше­нию к предыдущему.

Пределом обобщения являются категории. Категории в философии — это предельно общие, фундамен­тальные понятия, отражающие наиболее существенные, законо­мерные связи и отношения реальной действительности и позна­ния. К ним относятся категории: материя и движение, простран­ство и время, сознание, отражение, истина, тождество и проти­воречие, содержание и форма, количество и качество, необходи­мость и случайность, причина и следствие и др.

Ограничить понятие — значит перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но большим содержанием. Чтобы, например, ограничить понятие «юрист», мы переходим к понятию «следователь», которое в свою очередь можем ограничить, образо­вав понятие «следователь прокуратуры». Пределом ограничения по­нятия является единичное понятие (например, «следователь проку­ратуры Иванов»).

В процессе обобщения и ограничения понятий следует отличать переходы от рода к виду, от отношений целого к части (и наоборот). Так, например, неправильно обобщать понятие «центр города» до понятия «город» или ограничивать понятие «завод» до понятия «цех», так как в обоих случаях речь идет не об отношении рода и вида, а об отношении части и целого.

Операции с классами. Операции с классами — это такие логические действия, которые приводят нас к образованию нового класса.

Существуют следующие операции с классами: объединение, пересечение, вычитание, дополнение.

Объединение (или сумма) двух классов — это класс тех элементов. которые принадлежат хотя бы к одному из этих двух классов. Объединение обозначается: А + В или А U B. Объединение класса четных чисел с классом нечетных чисел дает класс целых чисел.

При выражении операции объединения классов пользуются, обычно союзом «или» в исключающем смысле. Например, говоря, что некто — член волейбольной или гимнастической сек­ции, мы не исключаем того, что этот человек может быть одновременно членом обеих секций.

В языке существует и такое употребление союза «или», при котором этот союз понимается в строго разделительном смысле, например: «Данный глагол первого или второго спряжения» Соответствующая операция над классами называется симмет­рической разностью.

При объединении могут встретиться следующие 6 случаев (рис. 1 —6).

Тождество Подчинение Пересечение

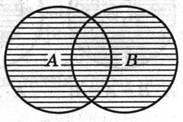
А + В = А = В А + В = А А + В

Рис. 1 Рис. 2 Рис. 3

Соподчинение Противоположность Противоречие

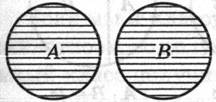
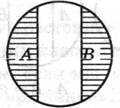
А + В А + В А +В

Рис. 4 Рис. 5 Рис. 6

Общей частью или пересечением двух классов называется класс тех элементов, которые содержаться в обоих данных множествах, т.е. это множество (класс) элементов, общих обоим множествам.

Пересечение обозначается А * Вили А∩В; ø — пустое множество. При пересече­нии могут встретиться следующие 6 случаев (см. рис. 7 – 12, где результат пересечения заштрихо­ван).

Тождество Подчинение Пересечение

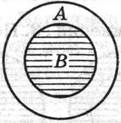
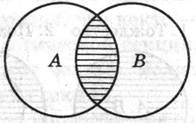
А * В = А =В А * В = В А * В

Рис. 7 Рис. 8 Рис. 9

Соподчинение Противоположность Противоречие

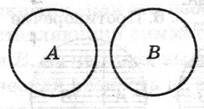
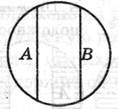
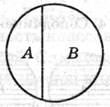
А *В = ø А *В = ø А *В = ø

Рис. 10 Рис. 11 Рис. 12

Поиск по сайту: