Определение срока ссуды и величины процентной ставки

При разработке условий контрактов или их анализе и сравнении возникает необходимость в решении ряда задач, связанных с определением срока ссуды и размера процентной ставки в том или ином ее виде при прочих заданных условиях.

Срок ссуды. В этом случае задача ставится таким образом, что требуется найти временной интервал, за который исходная сумма при заданной ставке процентов вырастет до нужной величины; или срок, обеспечивающий определенный дисконт с заданной величины. Другими словами, речь идет о решении формул (1.3) и (1.4) относительно n. Срок в годах:

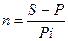(при использовании простой ставки наращения i);

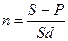(при использовании учетной ставки d).

Срок в днях (используется чаще, т.к. простые ставки используются в краткосрочных операциях) выражается как t = nK, где K – временная база, т.е.

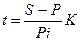или .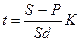

Пример 7. Какова должна быть продолжительность ссуды в днях для того, чтобы долг, равный 100 ден. ед., вырос до 120 ден. ед. при условии, что начисляются простые проценты по ставке 25% годовых (схема 365/365)?

Решение. По формуле находим: 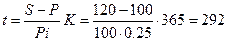дня.

Величина процентной ставки. Уровень процентной ставки может служить мерой доходности операции, критерием сопоставления альтернатив и выбора наиболее выгодных условий. Из тех же формул (1.3) и (1.4) получаем ставку наращения i и учетную ставку d для сроков, измеренных в годах и днях:

,

.

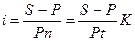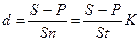Надо заметить, что срок в этих формулах имеет разный смысл: в первом случае это весь срок операции, а во втором – оставшийся срок до погашения.

Пример 8. Определить доходность операции для кредитора, если им предоставлена ссуда в размере 2 млн. руб. на 100 дней и контракт предусматривает сумму погашения долга 2,5 млн. руб. Доходность выразить в виде простой ставки процентов i. Временную базу принять равной 360 дней.

Решение. Воспользуемся полученной формулой: , т.е. 90%.

Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли от суммы погасительного платежа (процента скидки или общей учетной ставки). Таким образом, уровень процентной ставки здесь задается в неявном виде. Нетрудно вывести формулы, с помощью которых значения этих ставок можно вычислить.

Пусть S - размер погасительного платежа, d_n - доля этого платежа, определяющая величину дисконта за весь срок ссуды n. Требуется определить, каким уровням годовых ставок i и d эквивалентны такие условия.

Итак, S – сумма возврата в конце срока ссуды, P = S (l – d_n) – реально выдаваемая ссуда в момент заключения договора. Получаем:

,

.

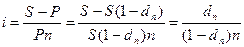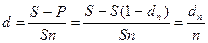Пример 9. Стороны договорились, что что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой ставки простых процентов i. Считать временную базу К равной 365 дням.

Решение. Воспользуемся полученными формулами:

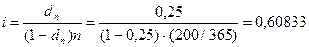, т.е. 60,833%,

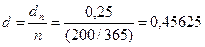, т.е. 45,625%.

Поиск по сайту: