АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Построение однофакторных уравнений линейной регрессии

Читайте также:
  1. MathCad: построение, редактирование и форматирование графиков в декартовой системе координат.
  2. MathCad: способы решения системы уравнений.
  3. V. Построение одного тренировочного занятия
  4. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  5. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  6. XI. Метод регрессии
  7. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  8. Арифметические выражения и алгоритм линейной структуры
  9. Вопрос 2. Построение доверительного интервала при неизвестном законе генерального распределения.
  10. Вопрос№5 Движение по окружности. Связь угловой и линейной скорости
  11. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
  12. Второе важное обстоятельство - преобразования Галилея меняют вид уравнений Максвелла

Для факторов х2 и х3 однофакторные уравнения линейной регрессии имеют вид:

 

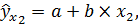(3.1)

 

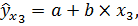(3.2)

 

где 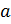–– параметр, представляющий значение у при х равном нулю;

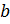–– коэффициент регрессии указывающий направление связи.

Параметры однофакторного уравнения регрессии находятся по формулам:

 

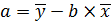, (3.3)

 

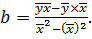(3.4)

 

Используя формулы (3.3) и (3.4) рассчитаем параметры для уравнения (3.1)

 

 

 

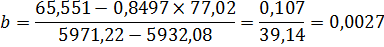
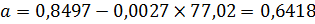
Используя формулы (3.3) и (3.4) рассчитаем параметры для уравнения (3.2)

 

 

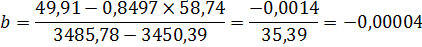
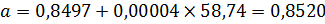
Таким образом используя рассчитанные коэффициенты получим однофакторные уравнения линейной регрессии:

 

 

 

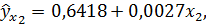
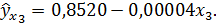
Коэффициенты детерминации рассчитываются по формуле:

 

 

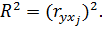
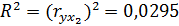или 2,95% –– доля факторной дисперсии в общей является низкой.

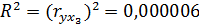или 0,0006% –– доля факторной дисперсии в общей практически отсутствует.


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)