Т е о р и я м е т о д а. Вращательное движение твердого тела характеризуется углом поворота j, угловой скоростью ,угловым ускорением ,вращательным моментом

Вращательное движение твердого тела характеризуется углом поворота j, угловой скоростью , угловым ускорением 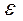, вращательным моментом и моментом инерции где

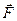-действующая сила, 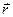-радиус вектор, m_i –масса любой точки тела.

Основное уравнение динамики вращательного движения выражает связь между М, J, 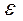М = J× 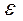(1)

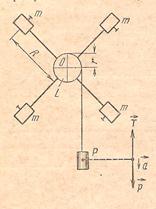рис.1.

Крестообразный маятник состоит из шкива ра-диуса r, закрепленного на оси О, четырех стерж-ней, расположенных под углом 900 друг к другу и 4-х муфт, которые могут перемещаться и зак-репляться на стержень в нужном положении. Момент инерции системы можно менять, пере-мещая муфты (грузы) вдоль стержня. На шкив наматывается нить, к свободному концу которой крепится груз рис.1 массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение.

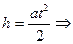
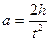
Угловое ускорение e может быть найдено, если измерить h и время падения t груза 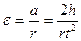(2)

здесь r - радиус шкива, на которую наматывают нить.

Из уравнения поступательного движения груза определим силу натяжения нити (силой трения пренебрегаем)

ma = mg – T 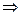T = mg – ma = m (g - a) (3)

Тогда вращательный момент М равен:

M = T× r = m(g-a)r (4)

Таким образом из уравнений (1), (2), (4) получаем экспериментальную формулу для определения момента инерции маятника

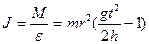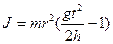Þ (5)

Момент инерции муфт находят опытным путем как разность моментов инерции системы (крестовины вместе с муфтами) J и крестовины без муфт J₀ J_м = J - J₀ (6)

Размеры муфт малы по сравнению с расстоянием R от оси вращения до центров масс грузов, поэтому теоретическое значение моментов инерции муфт равно J^¢_M = 4m₁R² (7)

где m₁ -масса одной муфты.

Поиск по сайту: