 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 8. Молекулярно - кинетическая теория идеальных газов
Молекулярная физика и термодинамика - разделы физики, в которых изучаются макроскопические (параметры) процессы в телах, связанные с огромным числом атомов и молекул, содержащихся в телах.
Для исследования этих процессов применяют два метода: статистический (молекулярно-кинетический) и термодинамический.
Молекулярная физика изучает строение и свойства вещества, исходя из молекулярно – кинетических представлений, основывающихся на том что:
1) все тела состоят из молекул
2) молекулы непрерывно и беспорядочно движутся
3) между молекулами существуют силы притяжения и отталкивания - межмолекулярные силы.
Статистический метод основан на том, что свойства макроскопической системы определяются, в конечном счете, свойствами частиц системы.
Термодинамика – изучает общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями и не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического метода. Основа термодинамического метода – определение состояния термодинамической системы.
Термодинамическая система – совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией между собой и внешней средой.
Состояние системы задается термодинамическими параметрами: p, V, T.
Применяют две шкалы температуры: Кельвина и Цельсия.
T = t + 2730 - связь между температурами t и Т
где t - измеряется в Цельсиях 0 С; Т - измеряется в кельвинах К.
В молекулярно – кинетической теории пользуются моделью идеального газа, согласно которой:
- собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда
- между молекулами газа отсутствуют силы взаимодействия
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Состояние идеального газа характеризуется 3 параметрами: p, V, T.
- уравнение Менделеева - Клайперона
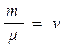или уравнение состояния идеального газа
здесь: - количество вещества [ моль ]
R = 8,31 - универсальная газовая постоянная
Опытным путем был установлен целый ряд законов, описывающих поведение идеальных газов.
Рассмотрим эти законы:
1) T – const – изотермический процесс
р
T –растет pV = const -
закон Бойля – Мариотта
V
2) 
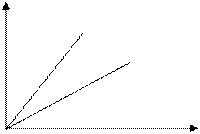p = const - изобарный процесс
V
p2-const - закон Гей - Люссака
p1 p2
p1>p2
Т
3) V – const – изохорный процесс
р
V1 - закон Шарля
V2
V1>V2
T
4) Закон Авогадро: моли любых газов при одинаковой температуре и давлении имеют одинаковые объемы.
При нормальных условиях: V = 22,4×10-3м3/моль
В 1 моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро
NA = 6,02×1023 моль-1
5) Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов.
p = p1 + p2 +... + pn – закон Дальтона
где p1, p2 ,... pn – парциальные давления.
- постоянная Больцмана k = 1,38 ×10-23 Дж/К
При одинаковых температурах и давлении все газы в единице объема содержат одинаковое число молекул.
Число молекул, содержащихся, в 1 м3 газа при нормальных условиях называется числом Лошмидта NL = 2,68×1025 м3
Нормальные условия: р0 = 1,013×103 Па
V0 = 22,4×10-3м3/моль
Т0 = 273 К
R = 8,31 Дж/мольК
На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяет вычислить давление газа, если известны m - масса молекулы газа, среднее значение квадрата скорости u2 и концентрация n молекул.
 |
- основное уравнение молекулярно-кинетической теории
Средняя кинетическая энергия поступательного движения молекул
 |
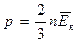Тогда - первое следствие из основного уравнения МКТ
- концентрация молекул
Температура – есть мера средней кинетической энергии молекул.
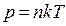Тогда - второе следствие из основного уравнения МКТ
Теперь запишем <u> - среднюю квадратичную скорость движения молекул
или
Средняя арифметическая скорость движения молекул определяется по формуле
или 
Молекулы, беспорядочно двигаясь, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь, который называется длиной свободного пробега.
Длина свободного пробега все время меняется, поэтому следует говорить о средней длине свободного пробега <l>, как о среднем пути, проходимом молекулой между двумя последовательными соударениями
 |
<z> - среднее число столкновений, испытываемых молекулой за 1с
<u> - средняя скорость.
Минимальное расстояние, на которое при столкновении сближаются центры двух молекул называется эффективным диаметром молекулы. – d.
 |
d
Среднее число столкновений за одну секунду равно числу молекул в объеме
<z> = nV, где n – концентрация молекул
V = pd2<u>
<z> =pd2n<u> при учете движения всех молекул
- средняя длина свободного пробега молекул
Тогда <z> =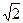 
pd2n<u> - среднее число столкновений молекул за 1 с.
Таким образом, <l> обратно пропорциональна концентрации молекул.
Тема 9. Статистические распределения
Из-за хаотического движения молекул все направления движения являются равновероятными, т.е. в любом направлении в среднем движется одинаковое число молекул. По молекулярно-кинетической теории как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул, находящихся в состоянии равновесия (Т=const), остается постоянной и равной
<υ> = 
Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически выведен Максвеллом. Максвелл предположил, что газ состоит из очень большого числа N молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Закон Максвелла описывается функцией f (υ) – функция распределения молекул по скоростям. Если разбить диапазон 
скоростей молекул на малые интервалы, равные dυ, то на каждый интервал скорости приходит некоторое число молекул dN (υ), имеющих скорость, заключенную в этом интервале. Функция f (υ) определяет относительное число молекул dN (υ) / N, скорости которых лежат в интервале от υ до υ + dυ,, т.е.
Отсюда 
Применяя методы теории вероятностей, Максвелл получил функцию
- закон о распределении молекул идеального газа по скоростям
Вид функции зависит от рода газа (m0. - массы молекулы) и от температуры. Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью
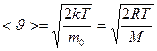
Исходя из распределения молекул по скоростям, можно найти распределение молекул по энергиям теплового движения
Проинтегрировав это выражение, получим среднюю кинетическую энергию молекул идеального газа 
При выводе основного уравнения МКТ и максвелловского распределения, предполагалось, что на молекулы газа не действуют внешние силы, поэтому молекулы равномерно распределены по объему. Мы знаем, что молекулы любого газа находятся в поле тяготения Земли и давление газа с высотой убывает по закону 
Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то можно записать
- барометрическая формула
р – давление на высоте h.
Используя формулу р = n kT, барометрическую формулу можно преобразовать
n – концентрация молекул на высоте h
n0 - концентрация молекул на высоте h =0
Так как М = m0NA, а R = kNA
то 
где Еp = m0gh - потенциальная энергия в поле тяготения
Тогда 
- распределение Больцмана для внешнего потенциального поля.
Поиск по сайту: