Т е о р и я м е т о д а. Изменение состояния идеального газа связано с изменением его параметров

Изменение состояния идеального газа связано с изменением его параметров. Согласно 1 закона термодинамики, количество теплоты , сообщенное системе, идет на увеличение внутренней энергии системы 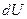и на совершение термодинамической работы

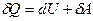(1)

Количество теплоты, необходимое для нагревания единицы массы вещества на один градус, называется удельной теплоемкостью:

(2)

Удельная теплоемкость газа зависит от условий, при которых происходит нагревание. Различают теплоемкости (удельную и молярную) при постоянном давлении (c_p и 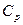) и при постоянном объеме (c_v и 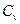). Для жидких и твердых тел, объем которых мало изменяется по сравнению с газом, значения 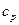и близки друг к другу по величине. Для разного рода практических расчетов их можно считать одинаковым. Сообщенное при постоянном давлении тепло идет на совершение работы и на изменение внутренней энергии, а при постоянном объеме – только на изменение внутренней энергии. Поэтому , а их отношение больше единицы и зависит от количества атомов, составляющих молекулу. Теплоемкости могут быть выражены через степени свободы молекул (число независимых переменных, полностью определяющих положение системы в пространстве):

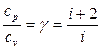(3)

Отношение теплоемкостей газа при постоянном давлении и постоянном объеме играет в термодинамике важную роль. В частности, оно входит в уравнение Пуассона, которое описывает адиабатный процесс.

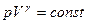(4)

Процесс, при котором отсутствует теплообмен между системой и окружающей средой, называется адиабатным, т.е. .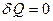

В случае адиабатного процесса из уравнения (1):

1) - работа внешних сил увеличивает внутреннюю энергию газа.

2) 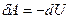- газ совершает работу за счет убыли внутренней энергии системы

Одним из простых методов определения пока-зателя адиабаты является метод Клемана-Дезорма. Экспериментальная установка сос-тоит из стеклянного баллона, соединенного с водяным манометром и насосом. Посредством крана баллон может быть соединен с атмосферой. Если в баллон накачать некоторое количество воздуха, то давление и температура в баллоне повысятся, но в результате теплообмена с внешней средой через некоторое время температура воздуха в баллоне сравнивается с температурой окружа-

ющей среды , а давление , где - атмосферное давление, - избыточное давление, измеряемое разностью уровней жидкости в манометре. Таким образом, первое состояние газа определяется параметрами , , . Если открыть кран на короткое время, то воздух будет расширяться до объема 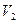, давление упадет до атмосферного и температура понизится до . Это будет второе состояние. Процесс перехода из состояния 1 в состояние 2 протекает очень быстро, поэтому его можно считать адиабатным. Согласно уравнению Пуассона или (5)

Через некоторое время газ нагреется вследствие теплообмена до температуры окружающей среды и давление возрастет до , где -новая разность уровней жидкости в манометре. Это новое третье состояние газахарактеризуется параметрами 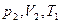. Так как в первом и третьем состояниях температура одинакова, то параметры этих состояний можно связать уравнением Бойля-Мариотта:

или (6)

Подставляя отношение объемов из уравнения (6) в уравнение (5) получим

Прологарифмируем это выражение и найдем показатель адиабаты

Так как значения давления мало отличаются друг от друга, в первом приближении разность логарифмов заменим разностью самих величин:

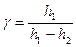или (7)

Поиск по сайту: