Т е о р и я м е т о д а

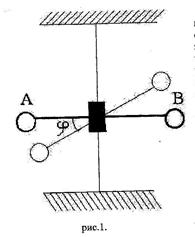
Крутильно-баллистический маятник (рис.1) представляет собой массивное тело А со значительным моментом инерции J, подвешенное на упругой нити. Если это тело повернуть в горизонтальной плоскости на угол j, то нить закручивается, в ней возникает упругий момент М, пропорциональный углу закручивания и стремящийся вернуть тело к равновесию. М =- k j (1) k - коэффициент пропорциональности, зависящий от упругихсвойств нити и геометрических размеров; j - угол закручивания; М – упругий момент.

Знак «-» означает, что крутящий момент направлен противоположно направлению закручивания. В результате тело будет совершать гармонические колебания. Кинетическая энергия маятника пере-ходит в потенциальную энергию упруго деформированной нити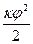

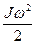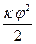= (2)

По основному закону динамики для вращательного движения крутящий момент М равен М = J×e (3)

J - момент инерции

e - угловое ускорение, равное второй производной от угла поворота.

e = j ²

Приравнивая уравнения (1) и (3) получим J×e = - kj или J×e +kj = 0.

Заменяя e на j ², получим J j ² + k × j или j ²+ 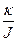× j = 0. Это уравнение описывает гармоническое колебательное движение, а 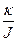= w². Угловая частота связана с периодом колебаний w= следовательно

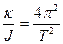
Маятник будет совершать колебания с периодом Т = 2p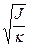

Колебания маятника начнутся после попадания снаряда в него. Момент импульса снаряда передается маятнику, т.е. переходит в момент импульса маятника

m× u× r = Jw_max (5)

m – масса снаряда

u – скорость снаряда

r - расстояние от точки попадания снаряда до центра вращения.

Из формулы (5) выражаем скорость полета снаряда

u = 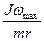(6)

Таким образом, для вычисления скорости полета снаряда необходимо измерить массу снаряда m и расстояние r от точки попадания снаряда до центра вращения.

Момент инерции маятника J и угловую скорость w_max определяем следующим образом:

Поиск по сайту: