 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 6 страница
Если система состоит из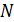 
частиц, то их среднее число 
в элементарном объёме 
вблизи точки 
равно
Чтобы получить локальную концентрацию молекул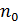 
в точке, разделим на элементарный объём
Объединив константы перед экспонентой, запишем окончательный вид формулы для пространственной концентрации молекул в потенциальном поле
Новая константа 
равна концентрации молекул в том месте, где 
.
Она может быть легко определена, если известна концентрация частиц, хотя бы в одной точке пространства. При отсутствии такой информации постоянную находят из условия нормировки на полное число частиц 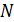в заданном объёме 
:
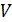При этом, подразумевается, что во всех точках объёма 
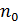концентрация должна быть одинаковой.
Изложенных выше сведений, относящихся к распределению Больцмана, вполне достаточно, чтобы приступить к рассмотрению зависимости концентрации молекул от координат в реальных силовых полях.
6.3. Зависимость концентрации молекул газа от координат в однородном гравитационном поле и поле центробежных сил
Ограничимся изучением распределения молекул в пространстве для двух важных в практическом отношении случаев: однородное гравитационное поле и поле центробежных сил.
На схеме 6.3.1 приведен параллельный вывод формул для концентрации молекул в этих полях, который позволяет легко вести сравнительный анализ исходных данных и результатов.
Схема 6.3.1.
Однородное гравитационное поле
Поле центробежных сил
Газ образует изотермическую атмосферу в однородном поле сил тяжести Рис. 6.1.
Потенциальная энергия молекулы на высоте z
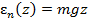, тогда
- концентрация на нулевом уровне (
). Число частиц в слое толщиной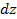 
в столбе газа с площадью сечения 
(рис. 6.1) равно
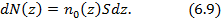
Рис. 6.1.
Полное число частиц в бесконечно высоком столбе
Газ находится в центрифуге, вращающейся с постоянной угловой скоростью 
. Геометрические параметры центрифуги приведены на Рис. 6.2.
Потенциальная энергия молекулы во вращающейся системе координат на расстоянии 
от оси вращения
тогда
- концентрация на оси вращения центрифуги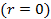 
. Число частиц в тонком цилиндрическом слое от до 
высотой 
равно
Рис. 6.2.
Полное число частиц в центрифуге
Графическое представление зависимости концентрации молекул от координат
На Рис. 6.3 можно сравнить вид зависимостей концентрации молекул газа от координат (6.8) и (6.11) для двух различных значений параметров системы. В случае поля тяжести (aи б) этими параметрами являются масса молекулы 
и температура газа 
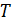. В поле центрифуги (в и г) – это её угловая скорость 
и температура газа .
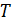а б
в г
Рис. 6.3.
6.4. Экспериментальное подтверждение распределения Больцмана: опыты Перрена
В начале ХХ века французский физик-экспериментатор Жан Батист Перрен решил проверить закон распределения Больцмана в лабораторных условиях, используя рукотворные крупные «молекулы», размер и массу которых можно измерить. Чтобы распределение таких частиц было наблюдаемым на небольшом интервале высот 
, их массы должны быть достаточно малыми, иначе они все окажутся на дне сосуда. Как сделать частицы крупными, но не тяжёлыми?
Перрен пришёл к заключению, что этого можно достигнуть, помещая частицы в жидкость, плотность которой лишь немного меньше плотности материала частиц, тогда поле тяжести будет сильно ослаблено архимедовой силой. При этих условиях можно считать, что частица обладает эффективной массой 
:
,
где 
– объём шарообразной частицы,
– плотность вещества частицы,
– плотность жидкости.
Перед Перреном встало несколько весьма трудных экспериментальных задач, с которыми он блестяще справился.
Получение макромолекул
Перрен получил макромолекулы из гуммигута, путём смешивания его со спиртом и многократного встряхивания, в результате чего им была получена эмульсия желтого цвета, в которой при наблюдении в микроскоп можно различить множество мелких шариков разного размера. Многократным разбавлением этой эмульсии водой была получена водная эмульсия шариков гуммигута.
Гуммигут – сгущённый млечный сок, получаемый из надрезов в коре некоторых видов южно-азиатских деревьев.
Выделение частиц одинакового размера
Для отбора шариков одинакового размера Перрен подвергал взвешенные в воде частицы многократному центрифугированию, в результате чего получил однородную эмульсию, состоящую из одинаковых шарообразных частиц с радиусом меньше микрометра.
Измерение диаметра макромолекулы
Прямым методом определить размеры частиц было невозможно, т.к. их диаметры были порядка или меньше длины световой волны, поэтому Перрен измерял длину ряда, составленного из известного и достаточно большого числа шариков вплотную прилегавших друг к другу. Путём деления полученной длину ряда на количество шариков в нём опредёлялся диаметр макромолекулы.
Подсчёт количества частиц на определённой высоте
Эмульсия помещалась в плоскую стеклянную кювету глубиной 0,1 мм и рассматривалась с помощью микроскопа.
Измерения нужно было производить при ничтожных разностях высот – несколько сотых миллиметра. Объектив микроскопа был сильного увеличения с малой глубиной фокуса, так что одновременно можно было видеть только частицы, находящиеся внутри очень тонкого горизонтального слоя с толщиной порядка микрометра.
Фокусируя микроскоп на определённый горизонтальный слой эмульсии, можно было сосчитать число частиц в этом слое. Разность высот измерялась микрометрическим винтом микроскопа. В результате эксперимента была подтверждена экспоненциальная зависимость
Эти уникальные опыты были выполнены в 1908 – 1911 годах и имели большое значение для утверждения идей молекулярной теории. Работы Перрена доказали применимость распределения Больцмана не только к молекулам, но и к макрочастицам. Измерения числа частиц на разных высотах позволили Перрену определить постоянную Больцмана и постоянную Авогадро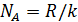 
. Полученное им на различных эмульсиях значение 
лежало в пределах 
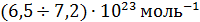, что находится в хорошем согласии со значениями, полученными впоследствии другими, более точными методами.
Напомним, что современное значение 
равно 
.
6.5. Барометрическая формула
Если рассматривать идеализированную изотермическую атмосферу, где 
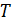и не зависят от высоты, тогда из формулы Больцмана для концентрации (6.8) и выражения для давления получим барометрическую формулу
На рисунке 6.4 показаны два графика 
) для одного и того же газа при разных температурах. Обратите внимание, что кривая 
начинается в одной точке независимо от температуры
Земная атмосфера не является равновесной, и меняются с высотой. Поэтому барометрическая формула (6.14) имеет очень ограниченную область применения.
| Рис. 6.4. |
где 
- давление в кПа, 
– высота в км. Эта формула получена эмпирическим способом при некоторых средних условиях, в частности, считается, что среднее значение температуры по высоте равно 
6.6. Закон распределения Максвелла – Больцмана
Вывод распределений Максвелла и Больцмана проводился нами дедуктивным методом из распределения Гиббса. Выросшие из одного корня, эти распределения могут быть объединены в одно – закон распределения Максвелла – Больцмана. Приведём одну из его формулировок.
Среднее значение молекул в объёме вблизи точки 
, имеющих проекции скорости в интервалах 
, 
, 
, определяется как
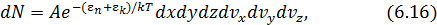
где 
Математическая структура и физический смысл (6.16) имеют простое толкование
,
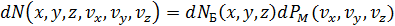– это общее число молекул в объёме (по Больцману) и оно умножается на долю молекул
проекции скоростей которых лежат в указанных выше интервалах (распределение Максвелла).
Если обе части уравнения (6.16) разделить на объём , то получим выражение для средней концентрации молекул 
в данном месте пространства 
, проекции скоростей которых находятся в соответствующих интервалах:
здесь использовано обозначение полной энергии молекулы 
. Формула (6.17) выражает распределение Максвелла – Больцмана в более компактной математической форме чем (6.16), не меняя его сути. При решении конкретных задач мы используем то или иное выражение закона, исходя из соображений удобства.
Контрольные вопросы
1. Какие внешние силовые поля совместимы с состоянием термодинамического равновесия статистической системы?
2. На какой вопрос отвечает распределение Больцмана? Запишите общий вид этого распределения.
3. Как определить константу в формуле для концентрации частиц в потенциальном поле?
4. Запишите формулы для концентрации частиц в однородном поле сил тяжести и в поле центробежных сил. Поясните смысл в каждом случае.
5. Постройте примерные графики зависимостей 
и 
.
6. Как подсчитать полное число частиц в центрифуге, зная зависимость 
?
7. Как подсчитать полное число частиц в бесконечно высоком столбе атмосферы ( =const), зная зависимость 
?
8. С какой целью в своих экспериментах Ж. Перрен смешивал шарики гуммигута с водой? Что из себя представляет гуммигут?
9. Какие экспериментальные задачи пришлось решать Ж. Перрену для подтверждения распределения Больцмана?
10. Значения каких величин определил Ж. Перрен в своих опытах? Получите формулы для нахождения этих величин.
11. Запишите барометрическую формулу. Какова область ее применимости?
12. Сформулируйте закон распределения Максвелла-Больцмана. Какова область его применимости?
ЛЕКЦИЯ 7
ТЕОРЕМА О РАВНОРАСПРЕДЕЛЕНИИ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ И ЕЁ ПРИЛОЖЕНИЯ
Прямые вычисления на основе распределения Максвелла убедительно показали, что на каждую степень свободы поступательного движения молекулы приходится одна и та же величина средней энергии равная 
.
Больцман обобщил этот факт в виде классической теоремы о равнораспределении средней энергии по степеням свободы. Теорема расширяет идею о равномерном распределении энергии для многоатомных молекул и идеальных твердых тел.
7.1. Формулировка теоремы и её доказательство
Формулировка теоремы
На каждую степень свободы статистической системы, находящейся в состоянии термодинамического равновесия, приходится одна и та же величина средней энергии:
Актуальные свойства модели статистической системы
• Система находится в состоянии термодинамического равновесия.
• Распределение энергии между малыми частями системы (молекулами и атомами) описывается распределением Гиббса.
• Массы частиц могут быть различными.
• Температура системы соответствует области применимости классических идеальных моделей материального тела.
Доказательство теоремы
В основе доказательства лежит тот факт, что выражение для всех видов внутренней энергии молекулы, приходящейся на одну степень свободы, имеет однотипную квадратичную форму: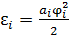 
, где 
– обобщённая координата, описывающая поступательное или вращательное движение молекулы как целого или колебательное движение отдельного атома в молекуле 
. Положительная константа 
описывает инертные или упругие свойства микроструктуры 
.
• Энергия молекулы
сумма всех квадратичных форм, исчерпывающе описывающая энергию сложной или простой частицы.
• Обратите внимание на то, что закон Гиббса применим к распределению энергии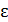 
, но не 
Другими словами выражение
• Получить правильное и простое решение (доказательство) можно путём перехода от распределения по энергиям 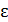к многомерному распределению по обобщённым координатам. Математическая структура этого распределения точно такая, как у распределения Максвелла в декартовой системе координат в пространстве скоростей.
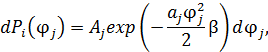
• Применим процедуру усреднения к квадрату обобщённой координаты:
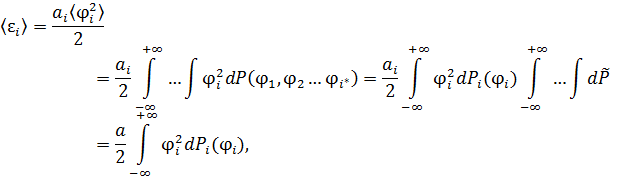
где 
, 
– по условию нормировки.
• Оставшийся интеграл легко берётся по частям
Что и требовалось доказать.
7.2. Статистические степени свободы
Опираясь на теорему равнораспределения энергии, можно сделать вывод, что для расчёта средней внутренней энергии любой молекулы идеального газа достаточно знать число квадратичных форм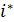 
в представлении её энергии в виде (7.1), тогда
Число 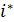принято называть числом статистических степеней свободы молекулы.
Для вычисления 
не надо брать никаких интегралов, надо только суметь подсчитать 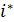. Это не сложно, поскольку 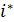зависит от механических степеней свободы 
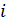. Различают поступательные 
, вращательные 
и колебательные 
степени свободы. Максимальное количество статистических степеней свободы многоатомной молекулы газа определяют следующим образом
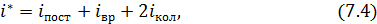
где 
(для нелинейной молекулы) или 2 (для линейной молекулы); 
определяют по остаточному принципу: 
. Полное число механических степеней свободы молекулы 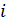всегда равно 
(
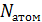– количество атомов в молекуле). Поясним на примере.
Подсчитаем 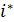для молекул водяного пара. Молекула 
состоит из трёх атомов (
), значит 
. Учитывая, что структура молекулы нелинейная, запишем
Следовательно, средняя энергия молекулы водяного пара
Теорема о равнораспределении используется при решении многих задач молекулярной физики, несмотря на достаточно ограниченную область температур, при которых она справедлива. Мы обсудим возможности применения теоремы при описании броуновского движения, а также при расчёте теплоёмкостей многоатомных газов и идеальных твёрдых тел.
7.3. Броуновское движение и его статистическое описание
Одним из экспериментальных подтверждений теоремы о равномерном распределении энергии по степеням свободы является броуновское движение. Явление было открыто английским ботаником Броуном в 1827 году.
Броуновское движение – этодвижение мельчайших частиц, взвешенных в жидкости или газе. Характер этого движения – хаотичное и непрерывное дрожание, которое можно наблюдать под микроскопом. Это движение никогда не прекращается. Интенсивность броуновского движения зависит от температуры среды, размеров частиц и некоторых других факторов.
Различают поступательное и вращательное броуновское движение. Полная теория броуновского движения была разработана в 1905 – 1906 гг. А.Эйнштейном и независимо польским физиком М. Смолуховским. Полученные ими результаты нашли экспериментальное подтверждение в измерениях Ж. Перрена и Т. Сведберга. Теория броуновского движения применяется в физической химии дисперсных систем (теория коагуляции растворов). В метрологии броуновское движение рассматривают как основной фактор, ограничивающий точность чувствительных измерительных приборов.
Поступательное броуновское движение
Это движение можно наблюдать с помощью микроскопа, рассматривая мелкие частицы (споры растений, частички краски, мелкие капли жидкости) взвешенные в воде или в другой жидкости. Прежде всего, отметим, что движения броуновских частиц совершенно не зависимы друг от друга.
Движение каждой взвешенной частицы происходит под действием случайной силы, возникающей за счет беспорядочных ударов молекул. Она получает толчки с разных сторон с какой-то стороны больше, с какой-то меньше. При этом ее скорость непрерывно меняется по величине и направлению. В результате этого частица двигается по очень сложной, изломанной траектории (рис. 7.1).
| Рис. 7.1. |
Поступательное броуновское движение характеризуется средним значением квадрата удаления частицы от начала координат 
в зависимости от времени движения 
. Статистический анализ случайных блужданий частицы приводит к простой формуле 
. Параметр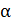 
можно найти из опыта или вычислить теоретически. Его теоретическое нахождение осуществляется решением уравнения движения частицы под действием случайной силы в вязкой среде. При этом используется условие, что на каждую степень свободы поступательное движение броуновской частицы приходится средняя энергия равная 
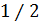kT.
Математическое выражение для , полученное таким способом, носит название формулы Эйнштейна-Смолуховского и имеет следующий вид
где 
– радиус шарообразной частицы, а 
– динамическая вязкость среды. Вывод (7.5) можно найти в [14,11].
Как видно из (7.5) средний квадрат удаления броуновской частицы за время линейно зависит от температуры, обратно пропорционален размеру частицы и вязкости среды. Обратите внимание, что тяжелые и легкие частицы имеют одинаковую среднюю скорость удаления от начала координат, хотя тяжелые частицы дрожат менее интенсивно, чем легкие.
Поиск по сайту: