АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Двумя концентрическими бесконечно длинными цилиндрами

Читайте также:
  1. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  2. Бесконечно - малые последовательности
  3. Бесконечно большие и бесконечно малые функции
  4. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
  5. Бесконечно большие функции и их связь с
  6. Бесконечно большие функции и их связь с бесконечно малыми функциями.
  7. Бесконечно малые и бесконечно большие функции
  8. Бесконечно малые функции
  9. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  10. Бесконечнозначная логика как обобщение многозначной системы Поста
  11. В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ
  12. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени

 

На рис. 16.6. изображена исследуемая система.

 

Однородная среда заполняет пространство между двумя цилиндрическими поверхностями с радиусами . Граничные условия стационарны:

 

Требуется найти зависимость температуры от расстояния от до аксиальной оси. Полный поток через цилиндрическую поверхность радиуса единичной длины равен

Этот поток является постоянной величиной, независящей от радиуса цилиндрической поверхности. Запишем это условие

 

Рис. 16.6.

Следовательно

 

 

Выразим левую часть этого уравнения согласно (16.1), тогда получим

 

 

После интегрирования (16.8) находим решение в общем виде

 

 

Константы 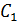и 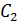находятся из граничных условий. При 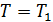, a при . Соответственно

 

 

Вычтем из второго уравнения первое и получим значение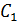

 

 

Подставив полученное выражение для 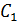в любое из уравнений (16.10) определим 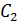. Окончательно решение имеет вид

 

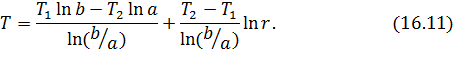
Стационарное распределение температуры


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)