 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Между двумя концентрическими сферами
На рис. 16.7. изображена исследуемая система.
| Рис. 16.7. |
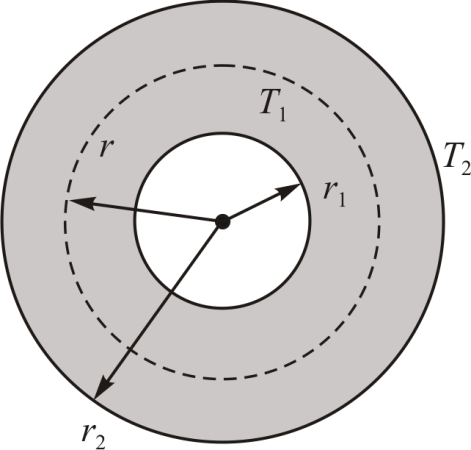 Пространство между сферами радиусов
Пространство между сферами радиусов 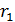 и
и  заполнено однородной средой. Поток теплоты через сферическую поверхность радиуса
заполнено однородной средой. Поток теплоты через сферическую поверхность радиуса  равен
равен 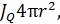 эта величина постоянна и не зависит от радиуса сферы. Поэтому уравнение для плотности потока имеет вид
эта величина постоянна и не зависит от радиуса сферы. Поэтому уравнение для плотности потока имеет вид

После интегрирования (16.12) получим
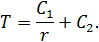
Из граничных условий находим 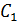 и
и 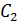 . Окончательно решение имеет вид
. Окончательно решение имеет вид
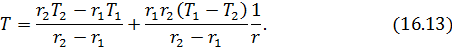
Ещё раз отметим, что распределения температур в слоях вещества с разной симметрией получены при условии, что 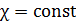 . Если это не так, то зависимость
. Если это не так, то зависимость 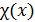 или
или  войдет в соответствующие дифференциальные уравнения. Это приведет к тому, что распределение температуры в слоях будет отличаться от (16.6), (16.11) и (16.13).
войдет в соответствующие дифференциальные уравнения. Это приведет к тому, что распределение температуры в слоях будет отличаться от (16.6), (16.11) и (16.13).
Внешняя теплопередача
Внешней теплопередачей называется теплопередача между двумя различными телами, не находящимися в тепловом равновесии друг с другом. Приведем примеры:
1. Процесс охлаждения нагретого металлического тела потоком воды или воздуха.
2. Процесс теплопередачи между отапливаемым домом и окружающим воздухом.
Идеализируя ситуацию, можно считать, что в каждый момент времени тело имеет одну и ту же температуру 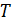 . Аналогично и окружающая среда может характеризоваться в каждый момент времени одной и той же температурой
. Аналогично и окружающая среда может характеризоваться в каждый момент времени одной и той же температурой 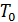 из-за происходящих в ней процессов перемешивания. В результате возникает тепловой поток через границу тел, обусловленный скачком температуры на этой границе. Нормальная составляющая этого потока
из-за происходящих в ней процессов перемешивания. В результате возникает тепловой поток через границу тел, обусловленный скачком температуры на этой границе. Нормальная составляющая этого потока  зависит от материала обеих сред, а также от их температур. При небольшой разности температур тела и среды выполняется закон Ньютона, который заключается в том, что плотность потока пропорциональна разности температур на границе тела с окружающей средой
зависит от материала обеих сред, а также от их температур. При небольшой разности температур тела и среды выполняется закон Ньютона, который заключается в том, что плотность потока пропорциональна разности температур на границе тела с окружающей средой

где 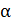 - коэффициент теплопередачи, нормаль
- коэффициент теплопередачи, нормаль 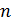 проведена от тела к среде. Опыты показали, что формула Ньютона (16.14) выполняется приближенно. Коэффициент теплопередачи является эмпирическим параметром и не представляет столь важную характеристику как теплопроводность среды.
проведена от тела к среде. Опыты показали, что формула Ньютона (16.14) выполняется приближенно. Коэффициент теплопередачи является эмпирическим параметром и не представляет столь важную характеристику как теплопроводность среды.
Контрольные вопросы
1. Какие процессы называются процессами переноса? Приведите примеры.
2. Почему переход системы к равновесию может характеризоваться несколькими, отличающимися друг от друга временами релаксации?
3. Что называется временем термализации?
4. Почему время релаксации зависит от размеров системы?
5. В чем суть представления о локальном равновесии?
6. Какое уравнение является основой молекулярно-кинетической теории явлений переноса?
7. Какая связь существует между процессами переноса и принципом Ле Шателье-Брауна?
8. Запишите стационарные одномерные уравнения теплопроводности, самодиффузии и внутреннего трения. Какова область их применимости?
9. Какова размерность коэффициентов теплопроводности, самодиффузии и вязкости?
10. Как зависит от координат плотность теплового потока в слое вещества, имеющем плоскую, цилиндрическую и сферическую симметрию?
11. Как используются граничные условия для нахождения распределения температуры в слое вещества?
12. Что называется внешней теплопередачей? Запишите формулу Ньютона, описывающую этот процесс. Какова область её применимости?
ЛЕКЦИЯ 17
ЭЛЕМЕНТАРНАЯ КИНЕТИЧЕСКАЯ ТЕОРИЯ
ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ
Настоящая лекция посвящена раскрытию сущности явлений переноса и нахождению количественных выражений для макроскопических коэффициентов переноса в плотных и ультра разреженных газах. Прежде чем приступить к изложению элементарной теории явлений переноса сконцентрируем свое внимание на рассмотрении столкновений молекул между собой. Именно эти микроскопические процессы играют определяющую роль в механизмах переноса молекулярных свойств, не только в газах, но также в жидкостях и твердых телах.
17.1. Столкновения молекул и их количественные характеристики
Столкновения частиц вещества друг с другом приводят к случайному изменению их кинетических энергий и, в конечном счете, к установлению равновесного распределения молекул по скоростям. Столкновения могут приводить и к другим последствиям. Например, в результате столкновения может произойти ионизация атома, химическая или ядерная реакции и многое другое. Если бы не было столкновений, то распространение запахов в воздухе и выравнивание температур в жидкостях и газах происходило бы практически мгновенно, ведь средние скорости теплового движения молекул равны сотням метров в секунду. В действительности при отсутствии конвективных потоков воздуха или жидкости продолжительность подобных процессов может составлять минуты и часы. Так же медленно происходит выравнивание скоростей макроскопического движения газа или жидкости посредством сил вязкости.
Медленность диффузии и аналогичных ей процессов объясняется тем, то в результате непрерывной череды соударений с другими частицами каждая молекула мечется туда и сюда и поэтому её продвижение вперед происходит не по прямой. Вспомните движение броуновской частицы. Траектория молекулы также изломана, как и линия, представленная на рис. 7.1. Для количественной характеристики интенсивности столкновений молекул используется четыре параметра:
1. Эффективное сечение молекулы  .
.
2. Средняя длина свободного пробега молекул  .
.
3. Среднее время между столкновениями  .
.
4. Средняя частота столкновений 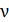 .
.
Все эти параметры связаны между собой.
Эффективное сечение молекул
Обычно, при рассмотрении столкновений одну частицу выделяют как движущуюся, а все остальные считаются неподвижными частицами-мишенями (рис. 17.1).
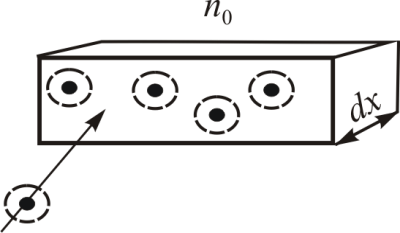
| Рис. 17.1. |
 относительно стенок сосуда, а средней относительной скоростью
относительно стенок сосуда, а средней относительной скоростью  двух произвольно взятых молекул. Прямое вычисление этой скорости с помощью распределения Максвелла дает результат:
двух произвольно взятых молекул. Прямое вычисление этой скорости с помощью распределения Максвелла дает результат:

Вероятность того, что движущаяся частица попадет в одну из частиц-мишеней при прохождении слоя толщиной 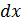 , пропорциональна величине
, пропорциональна величине 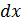 , а так же концентрации молекул-мишеней
, а так же концентрации молекул-мишеней 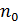 :
:

Коэффициент пропорциональности  имеет размерность площади (м2) и называется эффективным сечением молекулы. В общем случае
имеет размерность площади (м2) и называется эффективным сечением молекулы. В общем случае 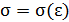 , т.е. зависит от энергии налетающей молекулы. В области применимости к молекулам классических моделей можно говорить, что
, т.е. зависит от энергии налетающей молекулы. В области применимости к молекулам классических моделей можно говорить, что  зависит от их средней относительной скорости движения. Таким образом, формула (17.1) определяет вероятность столкновения с конкретным результатом, который зависит от энергии соударяющихся частиц.
зависит от их средней относительной скорости движения. Таким образом, формула (17.1) определяет вероятность столкновения с конкретным результатом, который зависит от энергии соударяющихся частиц.
При столкновении молекула может изменить направление своего движения, т.е. рассеяться. Может поглотиться, диссоциировать молекулу или ионизировать атом, с которыми она сталкивается. В соответствии с этим говорят об эффективных сечениях рассеяния, поглощения, диссоциации, ионизации и пр.
В ядерной физике и физике элементарных частиц так же широко используется понятие эффективного сечения частицы по отношению к какому-либо процессу. Сильная зависимость  характерна для таких процессов как поглощение нейтронов атомными ядрами, деление тяжелых ядер под действием нейтронов, термоядерные реакции. Расчет эффективных сечений таких процессов возможен на основе законов квантовой механики. Для процессов переноса имеют значения только столкновения, приводящие к упругому рассеянию молекул и атомов на других молекулах и атомах. При этом внутреннее состояние сталкивающихся частиц не изменяется. Эффективное сечение таких процессов слабо зависит от
характерна для таких процессов как поглощение нейтронов атомными ядрами, деление тяжелых ядер под действием нейтронов, термоядерные реакции. Расчет эффективных сечений таких процессов возможен на основе законов квантовой механики. Для процессов переноса имеют значения только столкновения, приводящие к упругому рассеянию молекул и атомов на других молекулах и атомах. При этом внутреннее состояние сталкивающихся частиц не изменяется. Эффективное сечение таких процессов слабо зависит от  . Поэтому для его нахождения можно воспользоваться моделью твердых сфер и считать, что
. Поэтому для его нахождения можно воспользоваться моделью твердых сфер и считать, что 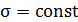 . На рис. 17.2. изображены две шароподобные молекулы в момент их соударения.
. На рис. 17.2. изображены две шароподобные молекулы в момент их соударения.
| Рис. 17.2. |
 Минимальное расстояние, на которое сближаются центры двух тождественных молекул при столкновении, называются эффективным диаметром молекулы
Минимальное расстояние, на которое сближаются центры двух тождественных молекул при столкновении, называются эффективным диаметром молекулы 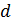 (рис. 17.2.). Площадь ограниченная пунктирной окружностью на рисунке равна эффективному сечению молекулы
(рис. 17.2.). Площадь ограниченная пунктирной окружностью на рисунке равна эффективному сечению молекулы  :
:

Если сталкивающиеся молекулы не тождественны, то

Параметр  так же называют газокинетическим эффективным сечением молекулы. Обратите внимание, что модель жестких сфер использовалась Ван-дер-Ваальсом для описания отталкивания в реальном газе, но у Ван-дер-Ваальса были еще и силы притяжения между молекулами. Таким образом, в допущении
так же называют газокинетическим эффективным сечением молекулы. Обратите внимание, что модель жестких сфер использовалась Ван-дер-Ваальсом для описания отталкивания в реальном газе, но у Ван-дер-Ваальса были еще и силы притяжения между молекулами. Таким образом, в допущении 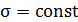 таится модель идеального газа. Сёзерленд в 1893 году учел силы притяжения, с которыми молекулы действуют друг на друга в промежутках между столкновениями. Он пришел к выводу, что силы притяжения, сближая молекулы, пролетающие мимо друг друга, делают возможными те столкновения, которые без притяжения не случились бы. Это приводит к увеличению
таится модель идеального газа. Сёзерленд в 1893 году учел силы притяжения, с которыми молекулы действуют друг на друга в промежутках между столкновениями. Он пришел к выводу, что силы притяжения, сближая молекулы, пролетающие мимо друг друга, делают возможными те столкновения, которые без притяжения не случились бы. Это приводит к увеличению  .
.
Роль притяжения проявляется при малых относительных скоростях движения молекул, т.е. при низких температурах. Эксперименты обнаруживают некоторое уменьшение эффективного сечения молекул с ростом температуры. В своей теории Сёзерленд получил формулу, носящую его имя, для среднего эффективного сечения молекулы реального газа

где,  вычисляется согласно выражению (17.2), а
вычисляется согласно выражению (17.2), а 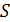 – постоянная, называемая постоянной Сёзерленда.
– постоянная, называемая постоянной Сёзерленда.
Средняя длина свободного пробега молекулы
Продолжим анализ формулы (17.1). Вероятность столкновения, как можно заметить, растет пропорционально пройденному молекулой пути 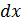 . Длина пути
. Длина пути  , при которой эта вероятность равна единице, называется средней длиной свободного пробега молекул.
, при которой эта вероятность равна единице, называется средней длиной свободного пробега молекул.
Согласно (17.1) получаем равенство

из которого следует, что

Формула (17.5) справедлива, если система состоит только из тождественных молекул. Если молекулы в системе разные, то надо учесть вероятность столкновений, как тождественных молекул, так и разных молекул друг с другом. В этом случае
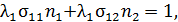
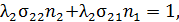
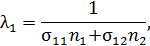
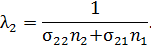
Здесь 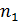 и
и 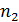 - концентрации молекул двух компонент;
- концентрации молекул двух компонент; 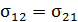 ;
;  и
и 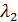 –средняя длина свободного пробега молекул компоненты 1 и компоненты 2 соответственно.
–средняя длина свободного пробега молекул компоненты 1 и компоненты 2 соответственно.
Кинематические параметры  и
и 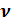
Из определения параметров  и
и  естественным образом определяются параметры
естественным образом определяются параметры  и
и 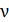 . Действительно среднее время между двумя столкновениями – это путь, деленный на среднюю скорость:
. Действительно среднее время между двумя столкновениями – это путь, деленный на среднюю скорость:

Тогда средняя частота столкновений будет равна

Сделаем количественную оценку четырех кинематических параметров на примере молекулярного азота при нормальных условиях, т.е. в приближении идеального газа:

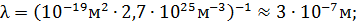
Здесь использовалось число Лошмидта 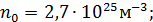
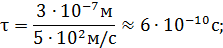
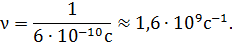
После рассмотрения характеристик столкновений молекул нашей ближайшей задачей будет установление связи между макроскопическими коэффициентами переноса в идеальном газе с его кинематическими параметрами.
17.2. Обобщенное уравнение переноса
Решение поставленной задачи будет базироваться на выводе обобщенного уравнения переноса. Используемый для этой цели метод средней длины свободного пробега является оценочным. Главное достоинство такого подхода состоит в его простоте и акценте на физической сущности явления. Ожидаемые результаты могут отличаться от точных числовыми коэффициентами. Точные решения следуют из кинетического уравнения Больцмана.
Вывод обобщенного уравнения процесса
Описание системы
Рассматриваемая система – идеальный газ в слабо неравновесном состоянии. 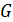 характеризует некоторое молекулярное свойство, отнесенное к одной молекуле газа (энергия, импульс, концентрация, электрический заряд).
характеризует некоторое молекулярное свойство, отнесенное к одной молекуле газа (энергия, импульс, концентрация, электрический заряд). 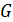 – функция координаты, медленно изменяющаяся вдоль одного направления, например
– функция координаты, медленно изменяющаяся вдоль одного направления, например 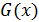 , но не зависящая от времени.
, но не зависящая от времени.
Актуальные свойства модели процесса
• При наличии градиента 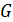 будет происходить движение или перенос
будет происходить движение или перенос 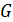 в направлении его уменьшения.
в направлении его уменьшения.
• Перенос 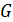 осуществляется встречными молекулярными потоками. Плотность этих потоков описывается известным уравнением эффузии
осуществляется встречными молекулярными потоками. Плотность этих потоков описывается известным уравнением эффузии
 .
.
• Функциональная зависимость G(x) не известна.
• Чтобы восполнить этот пробел воспользуемся разложением 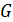 в ряд Тейлора в окрестности некоторой точки. В качестве малого параметра можно взять любую величину
в ряд Тейлора в окрестности некоторой точки. В качестве малого параметра можно взять любую величину 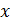 :
: 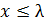 . Неравенство приведет впоследствии к неопределенности числового множителя в уравнении переноса.
. Неравенство приведет впоследствии к неопределенности числового множителя в уравнении переноса.
Постановка задачи
Требуется получить обобщенное уравнение переноса на основе микроскопических представлений.
Вывод уравнения
• Величину малого параметра 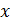 обычно берут равной
обычно берут равной  ,
, 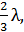
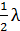 ,… Пусть
,… Пусть  .
.
• Изобразим встречные молекулярные потоки на схематическом рисунке (рис. 17.3), где ось  направлена вдоль градиента
направлена вдоль градиента 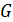 .
.

Рис.17.3.
• Величина  достаточно мала, поэтому
достаточно мала, поэтому 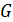 на таком расстоянии от 0 можно представить в виде:
на таком расстоянии от 0 можно представить в виде:

• Тогда, плотность потока 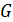 в направлении отрицательных значений оси Х запишем как
в направлении отрицательных значений оси Х запишем как
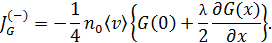
Плотность потока 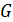 в направлении положительных значений оси
в направлении положительных значений оси  равна
равна
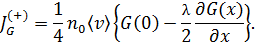
• Суммарная плотность потока в положительном направлении оси Х:
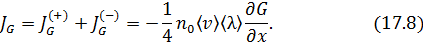
• При 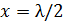 коэффициент получается равным
коэффициент получается равным 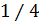 , а при
, а при 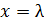 получается, что он равен
получается, что он равен 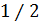 . В этом и проявляется неопределенность (приближенность) метода средней длины свободного пробега. Точное значение числового коэффициента находится из кинетического уравнения Больцмана и равно
. В этом и проявляется неопределенность (приближенность) метода средней длины свободного пробега. Точное значение числового коэффициента находится из кинетического уравнения Больцмана и равно 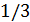 , учитывая это, запишем:
, учитывая это, запишем:

Это и есть обобщенное уравнение переноса.
17.3. Элементарная кинетическая теория теплопроводности,
самодиффузии и вязкости плотных идеальных газов
Получим уравнение теплопроводности, самодиффузии и вязкости, исходя из обобщенного уравнения переноса (17.9).
1. Пусть переносимым молекулярным свойством является внутренняя энергия идеального газа, приходящегося на одну молекулу:
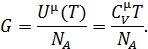
В этом случае обобщенное уравнение переноса переходит в уравнение теплопроводности
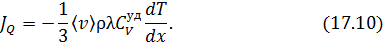
Выражение перед  в (17.10) и есть коэффициент теплопроводности
в (17.10) и есть коэффициент теплопроводности

Формула (17.7) выражает зависимость теплопроводности от микроскопических параметров  и
и  , а также от макроскопических параметров
, а также от макроскопических параметров  и
и  . Зависимость
. Зависимость  от температуры определяется средней скоростью
от температуры определяется средней скоростью 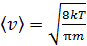 , т.е.
, т.е.  . Как видим, зависимость от температуры достаточно слабая и при решении некоторых задач можно пользоваться приближением, что
. Как видим, зависимость от температуры достаточно слабая и при решении некоторых задач можно пользоваться приближением, что 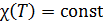 . А вот от давления теплопроводность плотных газов не зависит и не приближенно, а точно.
. А вот от давления теплопроводность плотных газов не зависит и не приближенно, а точно.
В этом легко убедиться. При фиксированной температуре в выражении (17.11) от концентрации частиц зависят два множителя: 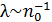 и
и 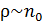 . Эти зависимости аннулируют друг друга.
. Эти зависимости аннулируют друг друга.
Для газов при нормальных условиях  лежит в интервале
лежит в интервале 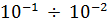 Вт/м·с. Например,
Вт/м·с. Например, 
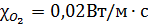 .
.
2. Пусть переносимое молекулярное свойство – концентрация «меченных» атомов, приходящаяся на одну молекулу фона:
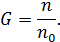
В этом случае обобщенное уравнение переноса переходит в уравнение самодиффузии

Выражение перед  в (17.2) представляет коэффициент самодиффузии
в (17.2) представляет коэффициент самодиффузии

Как видим 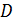 явно зависит только от микроскопических параметров. Зависимость от температуры и давления газа «зашита» внутри этих параметров. Поскольку
явно зависит только от микроскопических параметров. Зависимость от температуры и давления газа «зашита» внутри этих параметров. Поскольку 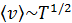 , то и
, то и  . В свою очередь
. В свою очередь 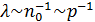 , соответственно и
, соответственно и 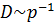 . Для газов при нормальных условиях
. Для газов при нормальных условиях 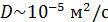 .
.
3. Пусть переносимое молекулярное свойство - это импульс упорядоченного движения одной молекулы:

В этом случае обобщены уравнение переноса переходит в уравнение внутреннего трения или вязкости

Следовательно, коэффициент вязкости  равен
равен

Функциональная зависимость  от температуры и давления подобна зависимости теплопроводности от этих параметров. Порядок величины
от температуры и давления подобна зависимости теплопроводности от этих параметров. Порядок величины  в газах при нормальных условиях составляет
в газах при нормальных условиях составляет 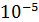 Па·с.
Па·с.
Вы без особого труда самостоятельно можете получить формулы, выражающие один коэффициент переноса через любой другой. Это дает возможность из исследования только какого-то одного явления переноса получить информацию о других процессах переноса. Экспериментальные измерения макроскопических коэффициентов переноса и полученные для них выражения в рамках кинетической теории (17.10), (17.13) и (17.15) позволяют определить такие микроскопические параметры как  ,
,  и
и 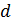 . Подобные экспериментальные задачи включены в программу практикума по молекулярной физике.
. Подобные экспериментальные задачи включены в программу практикума по молекулярной физике.
Физическая сущность таких явлений как теплопроводность и вязкость состоит в том, что в процессе столкновений молекул энергия теплового движения (теплопроводность) и импульс упорядоченного движения (вязкость) передаются от частицы к частице, от слоя к слою как эстафетная палочка. Несмотря на то, что частицы пребывают в хаотическом движении и беспорядочной толкотне, возникает упорядоченное движение определенного молекулярного свойства – поток энергии или поток импульса.
17.4. Явления переноса в ультраразреженных газах
Состояние разреженного газа называют вакуумом. Степень разрежения характеризуют тремя параметрами: 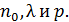 Понятие вакуума относительно, чем больше размеры области, тем при меньшем давлении он достигается. В теоретических рассмотрениях обычно используется сравнение величины
Понятие вакуума относительно, чем больше размеры области, тем при меньшем давлении он достигается. В теоретических рассмотрениях обычно используется сравнение величины  с линейным размером сосуда
с линейным размером сосуда 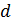 , ограничивающего объем газа. Принято различать четыре степени вакуума. Признаки градации и соответствующие названия вакуума приведены в табл. 17.1.
, ограничивающего объем газа. Принято различать четыре степени вакуума. Признаки градации и соответствующие названия вакуума приведены в табл. 17.1.
Таблица. 17.1.
Соотношение 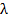 и и 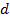
|

|
| низкий |
| Вакуум |
| средний |
| глубокий (высокий) |

|
| ультраразреженный (сверхвысокий) |
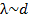
|
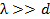
|
| Степени разрежения газа |
Для описания явлений переноса наиболее «прозрачным» является случай ультраразреженного газа. Поскольку в этих условиях столкновения между молекулами практически отсутствуют, то и «эстафетный» механизм передачи молекулярных свойств не работает. Молекулы по прямым линиям летят от одной стенки сосуда к другой и обмениваются с ними, например, энергией (это уже не теплопроводность, а теплопередача) или импульсом упорядоченного движения (трение при малых давлениях). Механизмы переноса можно легко смоделировать, используя уравнение эффузии.
Одной из особенностей высокого вакуума является невозможность возникновения в нем конвекционных потоков. Наиболее трудным для теории является случай среднего вакуума, когда 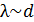 .
.
Трение и теплопроводность ультраразреженных газов
Независимость коэффициентов внутреннего трения и теплопроводности от давления газа, обоснованная нами в 17.3. имеет место при таких давлениях, когда 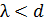 . В сильно разреженных газах, как отмечалось выше, механизм трения совершенно иной, нежели в плотных газах. Изменение импульсов молекул происходит только при ударах о стенку сосуда, поэтому трение становится не внутренним, а внешним. Внешнее трение зависит от числа ударов о стенку, которое пропорционально концентрации частиц, а следовательно, и давлению газа.
. В сильно разреженных газах, как отмечалось выше, механизм трения совершенно иной, нежели в плотных газах. Изменение импульсов молекул происходит только при ударах о стенку сосуда, поэтому трение становится не внутренним, а внешним. Внешнее трение зависит от числа ударов о стенку, которое пропорционально концентрации частиц, а следовательно, и давлению газа.
Аналогичное заключение можно сделать и по поводу теплопередачи. Молекула как пчела, несущая нектар, летит от горячей стенки к холодной и передает ей свою кинетическую энергию. После чего она «холодная и голодная» возвращается к горячей стенке за новой порцией энергии. Механизм выравнивания температуры именно таков. Количество перенесенной молекулами энергии пропорционально числу ударов о стенки, т.е. концентрации или давлению газа. Коэффициент теплопередачи растет пропорционально давлению.
Тепловая и изотермическая эффузия
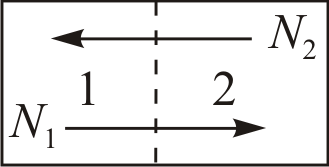
Интересные явления наблюдаются в сосудах с газом, сообщающихся через очень тонкую пористую перегородку. Размеры пор могут быть столь малыми (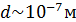 ), что в них соблюдаются условия вакуума уже при нормальном атмосферном давлении. Если по разные стороны перегородки имеется один и тот же газ и поддерживаются различные температуры, то наблюдается явление тепловой эффузии. А если по разные стороны перегородки находятся разные газы при одних и тех же начальных давлениях и температурах – наблюдается явление изотермической эффузии. На схеме 17.4.1 наглядно представлены необходимые начальные условия для тепловой и изотермической эффузии.
), что в них соблюдаются условия вакуума уже при нормальном атмосферном давлении. Если по разные стороны перегородки имеется один и тот же газ и поддерживаются различные температуры, то наблюдается явление тепловой эффузии. А если по разные стороны перегородки находятся разные газы при одних и тех же начальных давлениях и температурах – наблюдается явление изотермической эффузии. На схеме 17.4.1 наглядно представлены необходимые начальные условия для тепловой и изотермической эффузии.
Схема 17.4.1.
| Эффузия разреженных газов |
| Изотермическая |
 Начальные m 1 ≠m 2
условия: T 1 =T 2
p 1 =p 2
Начальные m 1 ≠m 2
условия: T 1 =T 2
p 1 =p 2
|
 Начальные m 1 ≡m 2
условия: T 1 ≠T 2
p 1 ≠p 2 или p 1 =p 2
Начальные m 1 ≡m 2
условия: T 1 ≠T 2
p 1 ≠p 2 или p 1 =p 2
|
| Тепловая |
Число частиц в эффузионном потоке через пористую перегородку в одном направлении равно

здесь произведение всех констант обозначено  . Результирующий поток складывается из двух встречных потоков
. Результирующий поток складывается из двух встречных потоков 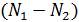 и
и
в равновесном состоянии равен нулю.
В случае тепловой эффузии, когда молекулы тождественны, равновесному состоянию согласно (17.15) соответствует равенство
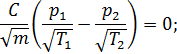
или

Очевидно, что в той половинке сосуда, где температура больше установится и более высокое давление. Это произойдет за счет увеличения концентрации частиц в «теплом» отсеке. Особенно наглядно это проявляется, если первоначально давления в разных отсеках были равны  . Газ начнет перетекать в направлении повышения температуры: от более низкой к более высокой температуре. Явление тепловой эффузии называют также эффектом Кнудсена. Перефразируя известную поговорку, можно сказать: «Рыба ищет, где глубже, а молекула – где теплее».
. Газ начнет перетекать в направлении повышения температуры: от более низкой к более высокой температуре. Явление тепловой эффузии называют также эффектом Кнудсена. Перефразируя известную поговорку, можно сказать: «Рыба ищет, где глубже, а молекула – где теплее».
В случае изотермической эффузии в начальный момент времени 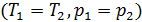 потоки
потоки 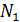 и
и  не равны:
не равны:

Если 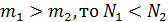 . Это значит, что более легкий газ будет быстрее проходить через пористую перегородку, чем более тяжелый. Образно говоря, стройные молекулы обгоняют молекулы толстушки. При
. Это значит, что более легкий газ будет быстрее проходить через пористую перегородку, чем более тяжелый. Образно говоря, стройные молекулы обгоняют молекулы толстушки. При  происходит одновременное выравнивание давления по обе стороны перегородки и концентрации молекул с разными массами. Зависимость
происходит одновременное выравнивание давления по обе стороны перегородки и концентрации молекул с разными массами. Зависимость  от времени по разные стороны перегородки показана на рис.17.4:
от времени по разные стороны перегородки показана на рис.17.4:
| Рис. 17.4. |
 Рассмотренные виды эффузии имеют практическое значение. Изотермическая эффузия лежит в основе одного из методов разделения изотопов. Тепловая эффузия играет важную роль в явлениях природы, обеспечивая обмен воздуха в почве, необходимый для нормальной жизни растений. Дадим пояснения этому практически значимому феномену.
Рассмотренные виды эффузии имеют практическое значение. Изотермическая эффузия лежит в основе одного из методов разделения изотопов. Тепловая эффузия играет важную роль в явлениях природы, обеспечивая обмен воздуха в почве, необходимый для нормальной жизни растений. Дадим пояснения этому практически значимому феномену.
Летом в дневное время суток поверхность земли нагревается солнечным излучением. Поэтому воздух из более глубоких и менее нагретых слоев почвы выходит по капиллярам природного происхождения наверх и разносится ветром. Ночью верхний слой земли охлаждается и возникает обратный поток воздуха с поверхности в более глубокие слои почвы. Таким образом, осуществляется суточная циркуляция воздуха в плодородных слоях земли.
В заключение темы отметим, что рассмотренные нами процессы переноса в газах не исчерпывают всех явлений такого рода. Например, в плотных газах мы обошли вниманием взаимную диффузию различных газов, а также термодиффузию. Остались в запасниках и некоторые явления в ультраразреженных газах, например, такие как течение Кнудсена, тепловое скольжение, радиометрический эффект. Вот уж воистину, чем больше узнаешь, тем больше граница с непознанным…
Контрольные вопросы
1. Назовите параметры, определяющие интенсивность столкновений молекул друг с другом.
2. Как определяется вероятность столкновения молекулы с другими частицами?
3. Что характеризует эффективное сечение молекулы?
4. Какого рода столкновения молекул определяют явления переноса?
5. Как определяется  в модели твердых тел?
в модели твердых тел?
6. Как определяется  в теории Сёзерленда?
в теории Сёзерленда?
7. Дайте определение средней длины свободного пробега молекул.
8. Назовите исходные положения, необходимые для вывода обобщенного уравнения переноса. Запишите это уравнение.
9. На основе обобщенного уравнения переноса получите выражение для а) теплопроводности; б) вязкости; в) коэффициента диффузии.
10. Раскройте физическую (микроскопическую) сущность явлений переноса.
11. Какие существуют градации состояний разреженного газа?
12. Назовите явления переноса в ультраразреженном газе, которые были рассмотрены на этой лекции? Какие эффекты и количественные соотношения для них характерны?
ЛЕКЦИЯ 18
АТМОСФЕРЫ ПЛАНЕТ
18.1. Атмосфера как открытая система и как открытая книга
Для молекулярной физики атмосферы планет представляют уникальные объекты исследования. Это гигантские газовые тела, не имеющие материальных границ и находящиеся в неоднородных гравитационных полях и потоках солнечного и галактического излучения. Атмосферы планет являются открытыми и существенно неравновесными системами. Температура в атмосфере планеты сложным образом зависит от координат. В атмосфере происходят разнообразные физические процессы и фотохимические реакции. Поэтому к планетной атмосфере в целом распределение Больцмана не применимо, так как при его выводе предполагалось, что газ находится в состоянии термодинамического равновесия с температурой, постоянной по всему объему газовой среды.
Исходя из представления о локальном равновесии (см.13.1), можно считать, что распределение Максвелла не теряет своей справедливости в квазиравновесных подсистемах. Вследствие распределения молекул по скоростям в атмосферах планет всегда имеется некоторое количество частиц, скорость которых больше второй космической скорости, зависящей от массы планеты. Так для Земли 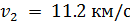 , для Луны
, для Луны 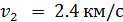 . Молекулы с такой скоростью способны преодолеть силу планетного притяжения, их называют убегающими молекулами. Эти молекулы находятся в «хвосте» распределения Максвелла, и их относительное число для планет с достаточно большой массой незначительно. Тем не менее, за большие промежутки времени потеря молекул является чувствительной, поскольку поток убегающих молекул постоянно пополняется за счет межмолекулярных столкновений.
. Молекулы с такой скоростью способны преодолеть силу планетного притяжения, их называют убегающими молекулами. Эти молекулы находятся в «хвосте» распределения Максвелла, и их относительное число для планет с достаточно большой массой незначительно. Тем не менее, за большие промежутки времени потеря молекул является чувствительной, поскольку поток убегающих молекул постоянно пополняется за счет межмолекулярных столкновений.
Вблизи планеты относительная концентрация убегающих молекул в этом потоке очень мала. По мере удаления от планеты их относительная концентрация возрастает. На бесконечности все молекулы являются убегающими. В конце концов, планета должна потерять свою атмосферу. Время  в течение которой масса атмосферы планеты убывает в е раз, называется временем рассеяния атмосферы. Приближенная оценка времени рассеяния идеализированной изотермической атмосферы для различных планет приводится в [12], согласно которой
в течение которой масса атмосферы планеты убывает в е раз, называется временем рассеяния атмосферы. Приближенная оценка времени рассеяния идеализированной изотермической атмосферы для различных планет приводится в [12], согласно которой  .
.
Изучение атмосфер планет в настоящее время ведется по трем направлениям.
Первое, традиционное направление, связанно с наземными и около земными наблюдениями объектов с использованием всеволновых телескопов и спектрометров. Анализ атомных и молекулярных спектров излучения по-прежнему является источником информации о составе и состоянии атмосферы. Основоположником этого направления по праву можно считать нашего великого соотечественника Михаила Васильевича Ломоносова. В июне 1761 года ученые всего мира с интересом наблюдали в телескоп одно из самых редких астрономических событий: прохождение Венеры по диску Солнца, но только Ломоносов обратил внимание на одну особенность этого явления. В момент вхождения планеты на диск Солнца, как и в момент схождения с него вокруг Венеры наблюдался светлый ореол – «тонкое как волос сияние» Ломоносов дал правильное научное объяснение этому феномену, считая его результатом преломления солнечных лучей в атмосфере Венеры. Так была открыта атмосфера Венеры и за сто лет до появления спектрального анализа было положено начало физическому изучению планет и их атмосфер.
Второе направление возникло сравнительно недавно. Оно базируется на измерениях физико-химический параметров атмосфер планет, получаемых с автоматических межпланетных станций (АМС), находящихся в непосредственной близости от исследуемых объектов.
В ХХ веке было проведено комплексное изучение планеты Венера с помощью советских АМС серии «Венера» (с 1961 по 1983 годы произведено 16 запусков станций) и американской АМС «Маринер - 10». Кстати, «Маринер - 10» исследовал также атмосферу Меркурия. Подытожили исследование атмосферы Венеры советские АМС «Вега-1» и «Вега-2». Программа исследования Марса была реализована на базе советских АМС серии «Марс» и американских – серии «Викинг». После чего началась программа НАСА «Вояджер». «Вояджер-1» успешно выполнил исследование Сатурна и его спутника Титана. «Вояджер-2» был направлен на самую окраину Солнечной системы к Урану и Нептуну. Как вам известно, в новом XXI веке успешно продолжается аппаратное исследование удаленных от Земли планет и их атмосфер. В частности, имеются в виду проекты Европейского космического агентства «Галилео» и «Кассини». Несмотря на колоссальную дороговизну подобных проектов, они реализуются и в результате человечество становиться обладателем уникальной и достоверной научной информации.
Наконец, третье направление представлено компьютерным моделированием крупномасштабных неравновесных процессов в атмосферах планет Солнечной системы. В этой области так же получены интересные и очень важные результаты. С некоторыми из них, относящимися к Земной атмосфере, мы познакомимся в дальнейшем более подробно.
18.2. Состав и структура атмосферы Земли.
Атмосфера нашей планеты образована смесью газов, влаги и частиц пыли и простирается до 3000 километров. Разумеется, верхняя граница выражена нечетко, так как с высотой газы разрежаются и постепенно переходят в мировое пространство. Сухой воздух у поверхности земли содержит 78,09% азота, 20,95% кислорода, 0,13% аргона и 0,03% углекислого газа. На долю всех остальных газов вместе взятых приходится всего лишь 0,01%. Относительный состав атмосферы до высот порядка ста километров существенно не меняется. Выше этой границы газы существуют в основном в атомарном состоянии. В самом верхнем слое от 300 до 3000 км присутствуют самые легкие ионы  и
и 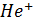 .
.
Хотя атмосфера простирается вверх на десятки сотен километров, основная масса воздуха сосредоточена в довольно тонком слое. Половина массы атмосферы находится между уровнем моря и высотой 5-6 км, а 99% - в слое до 30 км. Важные сведения о физических свойствах атмосфера получены с помощью космических аппаратов и геофизических ракет.
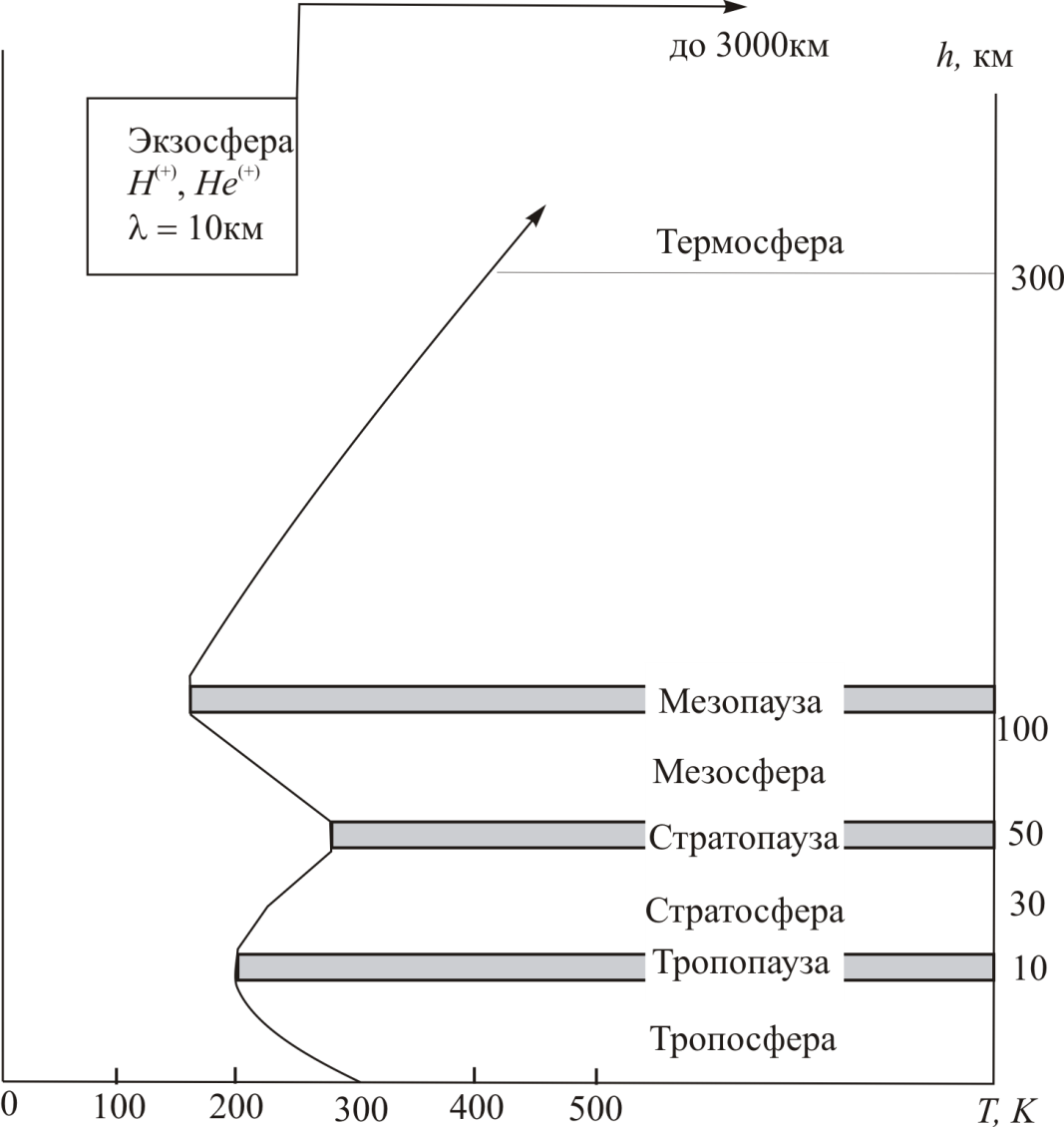
Рис. 18.1
Установлено, что с высотой изменяются не только атмосферное давление, плотность и температура воздуха, но и электрическое состояние атмосферы, а на больших высотах и ее состав.
Атмосфера земли подразделяется на несколько сфер с различными физическими свойствами. К числу этих сфер относятся: тропосфера, стратосфера, мезосфера, термосфера (или ионосфера), экзосфера (рис. 18.1).
Разделение на сферы производится на основе существующих градиентов температур, что явно прослеживается на выше приведенном рисунке. Обычно в тропосфере температура падает с увеличением высоты в среднем на 6º 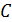 на каждый километр высоты проходит через минимум в тропопаузе, а затем в стратосфере возрастает с увеличением высоты и у верхней границы достигает значений, близких к 0º
на каждый километр высоты проходит через минимум в тропопаузе, а затем в стратосфере возрастает с увеличением высоты и у верхней границы достигает значений, близких к 0º 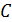 . Область, где температура растет с высотой, называется инверсионной или инверсионным слоем. Холодный воздух более плотный по сравнению с теплым, поэтому инверсионная область оказывается устойчивой к перемешиванию по вертикали. Это в полной мере относится к стратосфере. На интервале высот, называемом стратопаузой, температура проходит через максимум и затем падает в мезосфере, достигая второго минимума около - 80º С на уровне мезопаузы. На больших высотах в термосфере (80÷800 км) температура вновь растет с высотой, достигая значений 1500-2000
. Область, где температура растет с высотой, называется инверсионной или инверсионным слоем. Холодный воздух более плотный по сравнению с теплым, поэтому инверсионная область оказывается устойчивой к перемешиванию по вертикали. Это в полной мере относится к стратосфере. На интервале высот, называемом стратопаузой, температура проходит через максимум и затем падает в мезосфере, достигая второго минимума около - 80º С на уровне мезопаузы. На больших высотах в термосфере (80÷800 км) температура вновь растет с высотой, достигая значений 1500-2000 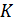 на высотах 500÷700 км.
на высотах 500÷700 км.
Выше термосферы расположена отделенная от нее термопаузой изотермическая область - экзосфера. Реальный профиль температуры может отличаться от приведенного на рис. 18.1 из-за особенностей места и времени, но в целом «картинка» верно передает характер закономерностей изменения температуры с высотой в атмосфере.
.
18.3. Термофизическая модель атмосферы
Под термофизической моделью будем понимать описание основных механизмов, объясняющих изменение температуры с высотой в атмосфере Земли. Раскрыть эти механизмы можно, опираясь на химический состав атмосферы на разных высотах и спектральный состав падающей от Солнца лучистой энергии.
Прежде всего, очень кратко сформулируем причины характерного изменения температуры в каждой из сфер атмосферы, начиная с самой нижней:
• Постоянство достаточно высокой температуры в нижних слоях тропосферы называется парниковым эффектом. Его природа будет раскрыта ниже.
• Отсутствие парникового эффекта в верхней тропосфере приводит к понижению температуры с высотой в тропосфере в целом.
• Инверсия температуры в стратосфере происходит вследствие экзотермических реакций озонового цикла в верхних слоях стратосферы.
• Уменьшение температуры в мезосфере связано с отсутствием там источников энергии.
• Рост температуры с высотой в термосфере объясняется близостью Солнца. Концентрация частиц в этом слое атмосферы на 5 порядков ниже, чем в тропосфере, поэтому здесь температура является характеристикой средней энергии отдельных частиц, а не макросистемы в целом;
• В экзосфере температура не зависит от высоты, полностью определяется солнечной радиацией и оставляет около 2000º 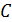 . Это переходная область между атмосферой Земли и околосолнечным пространством.
. Это переходная область между атмосферой Земли и околосолнечным пространством.
Из представленного выше списка разъяснения требуют только две причины и соответственно два механизма: парниковый эффект и реакции озонового цикла.
18.4. Парниковый эффект
Количественной характеристикой парникового эффекта является разность между средней поверхностной температурой атмосферы 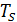 и её эффективной температурой
и её эффективной температурой  , т.е. температурой теплового излучения планеты, наблюдаемого из космоса. Таблица 18.1 позволяет сравнить величину парникового эффекта в атмосферах планет ближайших соседок Земли. Парниковый эффект существенен для планет с плотными атмосферами, содержащими газы, поглощающие излучение в инфракрасной области спектра, и пропорционален плотности атмосферы.
, т.е. температурой теплового излучения планеты, наблюдаемого из космоса. Таблица 18.1 позволяет сравнить величину парникового эффекта в атмосферах планет ближайших соседок Земли. Парниковый эффект существенен для планет с плотными атмосферами, содержащими газы, поглощающие излучение в инфракрасной области спектра, и пропорционален плотности атмосферы.
Для понимания сущности парникового эффекта в атмосфере необходимо сначала разобраться со спектральным составом солнечного излучения и способами его попадания в разные области газовой оболочки нашей планеты. На рис. 18.2 схематически представлен радиационно-тепловой баланс в атмосфере.
Основной состав падающего солнечного излучения это:
• видимый свет и ближний инфракрасный диапазон (с длиной волны 400÷1500 нм), составляет 75% энергии солнечного излучения;
• ультрафиолетовое излучение (λ > 300 нм).
После взаимодействия падающего излучения с земной поверхностью и её нагревания часть его преобразуется с появлением спектра частот в дальнем инфракрасном (ИК) диапазоне (λ = 8 ÷ 28 мкм).
Таблица. 18.1.
| Планета | Давление атмосферы у поверхности планеты, атм | 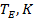
| 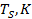
| 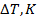
|
| Венера | ||||
| Земля | ||||
| Луна | ||||
| Марс | 0,006 |
Отраженное видимое и УФ-излучение уходят в космос, в то время как часть дальней ИК-составляющей при определенных условиях задерживается атмосферой, что и приводит к повышению температуры в нижних слоях тропосферы.
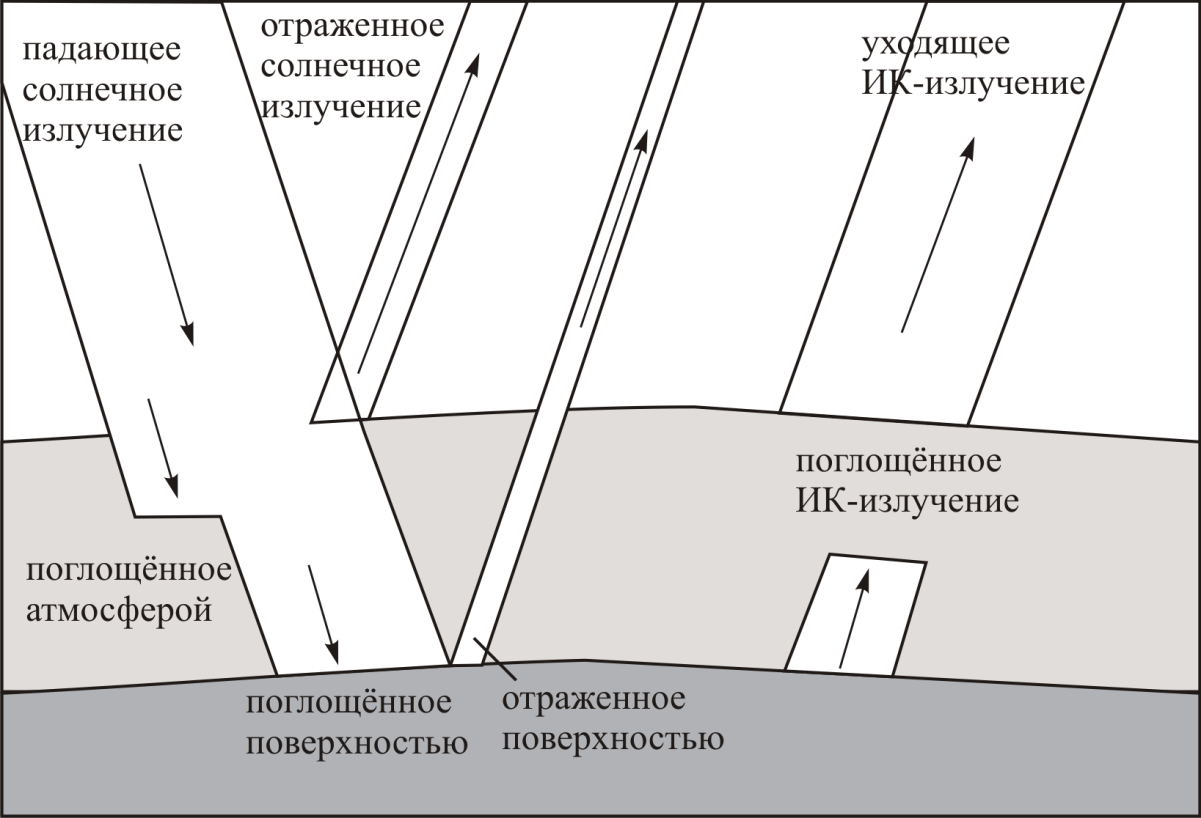
Рис. 18.2.
Сущность парникового эффекта
Если в атмосфере планеты присутствуют молекулы, обладающие колебательными степенями свободы уже при 0º  , то они поглощают энергию переизлученного поверхностью планеты радиационного потока в ИК-диапазоне, поскольку диапазон частот механических колебаний атомов совпадает с диапазоном инфракрасного излучения
, то они поглощают энергию переизлученного поверхностью планеты радиационного потока в ИК-диапазоне, поскольку диапазон частот механических колебаний атомов совпадает с диапазоном инфракрасного излучения
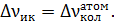
Преобразование энергии электромагнитного излучения ИК-диапазона в тепловую энергию колебаний таких молекул приводит к повышению температуры атмосферы в области их концентрации:
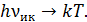
В этом и заключается сущность парникового эффекта.
Парниковые газы
У двухатомных молекул  колебательные движения появляются при очень высоких температурах (~103
колебательные движения появляются при очень высоких температурах (~103 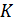 ). Поэтому они не могут создавать парниковый эффект. К парниковым газам относятся:
). Поэтому они не могут создавать парниковый эффект. К парниковым газам относятся: 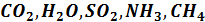 и любые другие молекулы с числом атомов больше двух.
и любые другие молекулы с числом атомов больше двух.
Вследствие парникового эффекта температура поверхности Земли поддерживается достаточно высокой и благоприятной для существования разнообразных форм органической жизни
Проблема глобального потепления
За последние 100 лет среднегодовая температура у поверхности Земли увеличилась на 1° 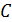 . В настоящее время в научных кругах существует две точки зрения на этот факт. Повышение температуры обусловлено
. В настоящее время в научных кругах существует две точки зрения на этот факт. Повышение температуры обусловлено
1) естественной флуктуацией климата,
2) усилением парникового эффекта за счет повышения концентрации парниковых газов техногенного происхождения.
Если вторая точка зрения верна, то стремительный рост концентрации парниковых газов может привести к катастрофическим последствиям: таянью полярных и горных ледников, повышению уровня мирового океана, затоплению обширных густозаселенных территорий суши, глобальному изменению климата. Даже если нет полной уверенности в такой перспективе общество обязано принять адекватные меры для уменьшения рисков.
Киотский протокол
В декабре 1997 года на встрече в Киото (Япония) делегатами из более чем ста шестидесяти стран была принята конвенция, обязывающая развитые страны сократить выбросы 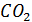 .
.
Киотский протокол обязывает тридцать восемь индустриально развитых стран сократить к 2012 году выбросы 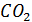 на 5% от уровня 1990 года.
на 5% от уровня 1990 года.
Протокол предусматривает систему квот на выбросы парниковых газов. Суть его заключается в том, что каждая из стран получает разрешение на выброс определенного количества таких веществ. Если какое-то государство превысит квоту выбросов, то в этом случае оно сможет купить право на дополнительные выбросы у тех стран, которые не превышают выделенной квоты. Россия ратифицировала Киотский протокол в конце 2007 года и с декабря 2008 года может продавать квоты странам-участникам соглашения, получая довольно высокие прибыли. Во исполнение Киотского протокола Россия обязуется создавать лесные плантации. Как известно, деревья поглощают парниковый углекислый газ 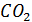 и выделяют в атмосферу не парниковый кислород
и выделяют в атмосферу не парниковый кислород 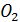 . В европейской части России уже началось создание «лесов Киото».
. В европейской части России уже началось создание «лесов Киото».
Между тем Киотский протокол не ратифицировали США – а именно на них приходится львиная доля вредных выбросов. Официальная причина – Штаты считают протокол неэффективным, так как в нем не принимают участие развивающие страны – Китай и Индия, чья доля выбросов тоже довольна велика.
18.5. Инверсия температуры в стратосфере. Озоносфера Земли
В середине прошлого века внимание исследователей атмосферы было привлечено к области, содержащей одну из химических модификаций кислорода – озон. Трехатомный молекулярный газ  имеет синий цвет и резкий запах. Он образуется из обычного кислорода
имеет синий цвет и резкий запах. Он образуется из обычного кислорода 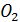 при электрических разрядах или под действием ультрафиолетового излучения.
при электрических разрядах или под действием ультрафиолетового излучения.
Большая часть озона, находящегося в атмосфере, расположена в стратосфере на высотах 10÷50 км с максимальной концентрацией 1012 – 1013 см-3 на высоте 20-30 км. Этот насыщенный озоновый слой называется озоносферой. При его образовании происходят следующие основные процессы [10].
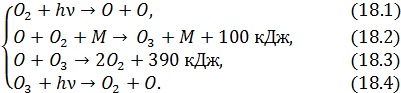
где 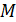 –какая-либо третья частица (обычно
–какая-либо третья частица (обычно  или
или 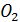 );
);  – энергия кванта ультрафиолетового излучения (
– энергия кванта ультрафиолетового излучения ( 290 нм), приводящая к фотодиссоциации молекул
290 нм), приводящая к фотодиссоциации молекул 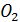 и
и  . Таким образом, молекулы озона поглощают энергию ультрафиолетового излучения с длиной волны
. Таким образом, молекулы озона поглощают энергию ультрафиолетового излучения с длиной волны 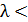 290 нм, спасая тем самым все живое на Земле от губительного жесткого ультрафиолета.
290 нм, спасая тем самым все живое на Земле от губительного жесткого ультрафиолета.
Следует отметить, что при образовании каждого моля озона согласно (18.2) высвобождается 100 кДж энергии и при разрушении каждого моля в реакции (18.3) выделяется ещё 390 кДж. Следовательно, в результате цикла реакций (18.1)-(18.4) в атмосферу выделяется большое количество теплоты, что и объясняет наблюдаемый в стратосфере рост температуры с высотой (рис. 18.3).
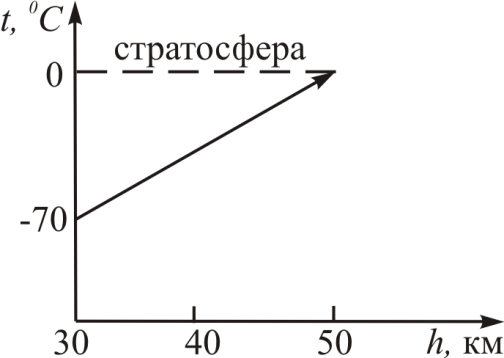
Рис. 18.3.
Естественно, что это фотохимическое нагревание атмосферы с образованием инверсионной области представляет большой интерес для метеорологов.
Мониторинг озонового слоя
Систематические измерения содержания озона в атмосфере начались в Англии и Швейцарии в 1926 году. Позднее начала формироваться мировая озонометрическая сеть, а в 60-е годы ХХ века появилась и советская сеть. В настоящее время в мире работают около 120 озонометрических станций, из них около 40 – на территории России.
В результатах измерений обычно приводят толщину озонового слоя в мм, это приведенная толщина, которую занимал бы  при нормальных условиях. Нормальной считается толщина слоя в 3,5 мм, если его истощение достигает более 25% - говорят об «озоновых дырах». В антарктической озоновой дыре истощение озона составляет более 50%. Существует гипотеза антропогенного разрушения озонового слоя.
при нормальных условиях. Нормальной считается толщина слоя в 3,5 мм, если его истощение достигает более 25% - говорят об «озоновых дырах». В антарктической озоновой дыре истощение озона составляет более 50%. Существует гипотеза антропогенного разрушения озонового слоя.
В 1996 году ученые Ш. Роуланд, М. Молина из Калифорнийского университета в США и П. Крутцен из Института химии им. Макса Планка в Германии были удостоены Нобелевской премии за установление причин снижения концентрации стратосферного озона. Они смогли доказать, что основными разрушителями озона являются атомы хлора или брома, отделившиеся под действием солнечной радиации от молекул, синтезированных человеком химических веществ, которые имеют очень широкое применение.
Например, при фотодиссоциации из фреона выделяется свободный атом хлор
Фреон + 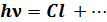
При этом только один атом 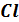 способен разрушить 104 молекул
способен разрушить 104 молекул 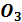 .
.
Монреальский Протокол
В октябре 1987 года в Монреале, 36 стран (СССР в 1988 году) подписали Протокол о сокращении производства опасных озоноразрушающих веществ. Международное соглашение предусматривало замораживание на уровне 1986 года производство пяти наиболее широко применяемых хлорфторуглеродов, а затем сокращение их производства на 20% к 1993 году и на 30% - к 1998 году
В ноябре 1992 года в Копенгагене были приняты новые поправки, в соответствие с которыми появилось требование о поэтапном выводе из производства метилбромида и гидрохлорфторуглерода.
К июню 1995 года почти 150 стран подписали Монреальский протокол, а на юбилейной встрече в Монреале в сентябре 1997 таких стран было уже 163.
В 1997 в Монреале договорились о необходимости введения лицензирования во всех странах соглашения экспортно-импортных операций с озоноразрушающими веществами, а также о сокращении сроков вывода из потребления метилбромида, который является очень дешевым и эффективным пестицидом. Страны-участники активно сотрудничают по реализации принятых на себя обязательств.
18.6. Концепция «ядерной зимы»
Поиск по сайту: