АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение внутреннего трения

Читайте также:
  1. V2: Волны. Уравнение волны
  2. V2: Уравнение Шредингера
  3. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  5. Анализ внутреннего имиджа МБДОУ «Детский сад №5».
  6. Аспект рассмотрения семьи
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. В уголовном судопроизводстве функция обвинения отделена от функции защиты, а обе они отделены от функции рассмотрения дела судом.
  10. Виды и процессуальные особенности рассмотрения дел в порядке особого производства
  11. Виды и процессуальные особенности рассмотрения дел, возникающих из публичных правоотношений
  12. ВИПАССАНА - МЕДИТАЦИЯ ВНУТРЕННЕГО ОЗАРЕНИЯ

Прежде чем записать уравнение внутреннего трения представьте себе неограниченную среду (газ или жидкость), движущуюся плоско-параллельными слоями в горизонтальном направлении. Скорость этого макроскопического движения меняется в направлении, перпендикулярном к слоям. Это направление примем за ось (Рис. 16.3).

 

 

Рис.16.3.

 

Допустим для определенности, что скорость возрастает с возрастанием 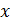. Рассечем мысленно среду на две половины плоскостью , параллельной слоям. Тогда верхняя половина среды будет действовать на нижнюю с силой, направленной вправо, а нижняя на верхнюю – с силой, направленной влево. Это и есть силы внутреннего трения или вязкость.

Уравнение внутреннего трения называется уравнением Ньютона

 

 

где 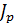- плотность потока импульса, - градиент скорости упорядоченного движения молекул, - коэффициент вязкости (динамическая вязкость). Размерности названных величин таковы:

 

 

Направления плотности потока импульса и противоположны (cмотрите поясняющий рис. 16.4).

 

Рис. 16.4.
Представленные выше уравнения переноса справед ливы для газов, жидкостей и твердых тел. Специфика системы «зашита» в коэффициентах переноса. Их значения зависят от внутренней структуры вещества и его состояния (температуры, давления). В рамках макроскопического подхода коэффициенты переноса определяют из экспериментов. Молекулярно-кинетическая теория позволяет получить значения этих коэффициентов с использованием соответствующих моделей материальных тел.

 

16.3. Внутренняя теплопроводность и внешняя теплопередача

Рассмотрим более детально явление теплопроводности, имеющее важное практическое значение. Формула (16.1), определяющая плотность потока теплоты, относится к случаю, когда распределение температуры в среде непрерывно и теплопроводность также является непрерывной функцией координат. Теплопроводность в этом случае называется внутренней теплопроводностью. В стационарном случае температура 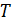не меняется от времени, а является функцией только пространственных координат. Поэтому все стационарные задачи на внутреннюю теплопроводность сводятся к двум вопросам. Требуется найти либо распределение температуры в среде с заданными граничными условиями, либо получить функциональную зависимость от координаты. Рассмотрим простейшие случаи, когда среда однородна и поэтому .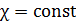

 

Стационарное распределение температуры

в бесконечной плоско-параллельной пластинке

Дана бесконечная пластинка толщины , поверхности которых поддерживаются при постоянных температурах 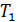и 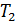.Она изображена на рис. 16.5. Требуется найти распределение температуры 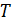внутри пластинки.

 

Рис. 16.5.
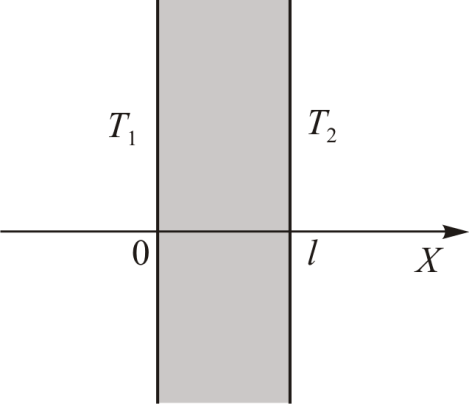Запишем (16.1) для этой задачи в виде

 

 

Если 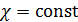, из (16.3) следует

 

 

После интегрирования (16.4) получим

 

 

где 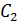- постояная интегрирования. Таким образом, температура меняется с координатой 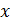по линейному закону. Константы 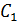и 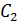находятся из граничных условий. При 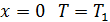, а при 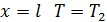. Соответственно 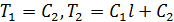. Найденные значения 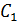и 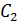подставим в (16.5) и получим формулу для распределения температуры в пластинке:

 

Стационарное распределение температуры между


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)