Уравнения, не содержащие явно искомой функции

и ее производных до порядка k – 1 включительно.

Это уравнения вида: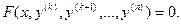

В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:

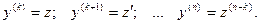
Тогда получаем:

Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:

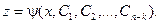
Делая обратную подстановку, имеем:

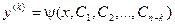
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:

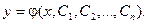
Пример. Найти общее решение уравнения .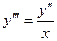

Применяем подстановку

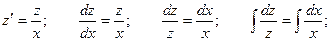
Произведя обратную замену, получаем:

Общее решение исходного дифференциального уравнения:

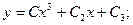
Отметим, что это соотношение является решением для всех значений переменной х кроме значения х =0.

Уравнения, не содержащие явно независимой переменной.

Это уравнения вида

Порядок таких уравнений может быть понижен на единицу с помощью замены переменных

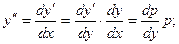
и т.д.

Подставляя эти значения в исходное дифференциальное уравнение, получаем:

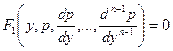
Если это уравнение проинтегрировать, и - совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка:

Пример. Найти общее решение уравнения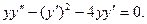

Замена переменной: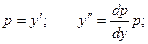

1)

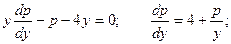
Для решения полученного дифференциального уравнения произведем замену переменной: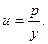

С учетом того, что , получаем:

Общий интеграл имеет вид: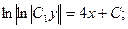

2)

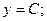
Таким образом, получили два общих решения.

Линейные дифференциальные уравнения высших порядков.

Определение. Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных 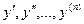вида:

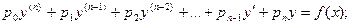
где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀ ¹ 0.

Левую часть этого уравнения обозначим L(y).

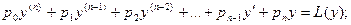
Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однородным уравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.

Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным.

Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков.

Поиск по сайту: