 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Линейные однородные дифференциальные уравнения с. постоянными коэффициентами
постоянными коэффициентами.
Решение дифференциального уравнения вида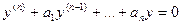 
или, короче, 
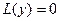будем искать в виде 
, где k = const.
Т.к. 
то
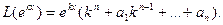
При этом многочлен 
называется характеристическим многочленом дифференциального уравнения.
Для того, чтобы функция являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы
т.е. 
Т.к. ekx ¹ 0, то 
- это уравнение называется характеристическим уравнением.
Как и любое алгебраическое уравнение степени n, характеристическое уравнение 
имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.
Не будем подробно рассматривать каждый случай, а сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.
1) Составляем характеристическое уравнение и находим его корни.
2) Находим частные решения дифференциального уравнения, причем:
a) каждому действительному корню соответствует решение ekx;
б) каждому действительному корню кратности m ставится в соответствие m решений:
в) каждой паре комплексно – сопряженных корней 
характеристического уравнение ставится в соответствие два решения:
и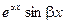 
.
г) каждой паре m – кратных комплексно – сопряженных корней характеристического уравнения ставится в соответствие 2 m решений:
3) Составляем линейную комбинацию найденных решений.
Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами.
Пример. Решить уравнение 
.
Составим характеристическое уравнение: 
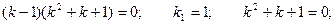
Общее решение имеет вид: 
Пример. Решить уравнение 
Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение.
Таким частным решением будет являться функция 
Исходное дифференциальное уравнение можно преобразовать:
Общее решение имеет вид: 
Окончательно: 
Пример. Решить уравнение 
Составим характеристическое уравн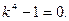ение: 
Общее решение: 
Пример. Решить уравнение 
Характеристическое уравнение: 
Общее решение: 
Пример. Решить уравнение 
Характеристическое уравнение: 
Общее решение: 
Пример. Решить уравнение 
Характеристическое уравнение: 
Общее решение: 
Пример. Решить уравнение 
Характеристическое уравнение: 
Общее решение: 
Пример. Решить уравнение 
Характеристическое уравнение: 
Общее решение: 
Пример. Решить уравнение 
Это уравнение не является линейным, следовательно, приведенный выше метод решения к нему не применим.
Понизим порядок уравнения с помощью подстановки 
Тогда 
Окончательно получаем: 
Это выражение будет общим решением исходного дифференциального уравнения. Полученное выше решение у1 = С1 получается из общего решения при С = 0.
Пример. Решить уравнение 
Производим замену переменной: 
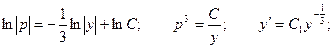
Общее решение: 
Поиск по сайту: