АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Графически получено оптимальное решение в точке М (4 ; 3 ) поэтому

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. O природно-географические
  7. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  8. Алгоритм решения ЗЛП графическим методом
  9. Аналитический подход к исследованию величин в критической точке
  10. Аналитическое решение
  11. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  12. Арбитражное разрешение международных споров в Древней Греции

 

S(4, 3, l10, l20, l30).

 

Для вычисления l10, l20, l3 запишем функцию Лагранжа F(x,l).

F(x,l)= 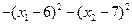+l1() +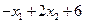

 

+ l2() +

 

+ l3()

 

Локальные условия Куна-Таккера:

 

 

 

 

 

 

 

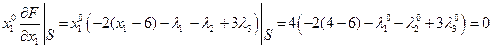
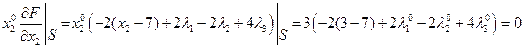
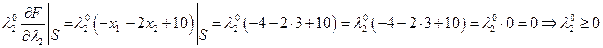
Подставим и в 1-е и 2-е уравнения:

Седловая точка функции Лагранжа: S .

 

Проверим условия cедловой точки:

 

 

Условия (*) выполнены.

 

Ответ: S – седловая точка.

 

91 - 100. Для двух предприятий выделено единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим. если известно, что доход от x единиц, вложенных в первое предприятие, равен , а доход от единиц, вложенных во второе предприятие, равен . Остаток средств к концу года составляет для первого предприятия и - для второго предприятия. Решить задачу методом динамического программирования.

№ зад.
100.   3 0,6 4 0,4

Решение. Процесс распределения средств разобъем на 4 этапа – по соответствующим годам.

Пусть i - сумма средств выделенных предприятиям в i-м году, xi - средства вложенные в первое предприятие в i-м году, yi – средства вложенные во второе предприятие в i-м году, тогда

 

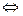i = xi + yi yi = i - xi

Остаток средств от обоих предприятий на i–ом шаге:

i+1 = g1 (xi) + g2 (yi) =g1 (xi) + g2 ( i - xi) = 0,6 xi + 0,4 ( i - xi) = 0,2xi + 0,4 i

 

Пусть Fi – cуммарный наибольший общий доход от обоих предприятий в i-м и последующих годах, тогда

 

Fi = =

= =

 

=

 

Пусть i = 5 тогда по условию F5 = 0.

i = 4, F4 = = = ,

т.к. линейная убывающая функция достигает наибольшего значения в начале рассматриваемого промежутка , т.е. при .

 

i = 3, F3 = = =

 

= ,

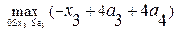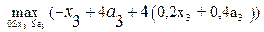т.к. линейная убывающая функция достигает наибольшего значения в начале промежутка, т.е. при .

 

 

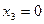i = 2, F2 = =

 

, т.к. линейная возрастающая функция достигает наибольшего значения в конце рассматриваемого промежутка, т.е. при .

 

i = 1, F1 = =

 

 

 

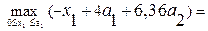
т.к. линейная возрастающая функция достигает наибольшего значения в конце рассматриваемого промежутка, т.е. при .

 

Итак наибольший общий доход F1 = =

 

Составим оптимальное распределение средств по годам

 

Т.к. ,

 

Далее получаем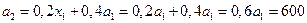

 

 

 

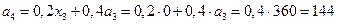
Остаток средств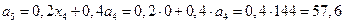

 

Годы Предпр.         Остаток
xi             57,6
yi          

 

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.009 сек.)