Нормированные сопротивления и проводимости

Отношение полного нормированного напряжения 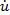к полному нормированному току 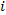в сечении 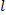эквивалентной длинной линии представляет собой эквивалентное полное нормированное сопротивление (безразмерное) в сечении 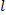линии:

(3.4)

Обратная величина является полной нормированной проводимостью (так же безразмерной):

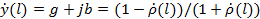(3.5)

В отличие от приведенных ранее выражений в (3.4) и (3.5) отсутствует волновое сопротивление, поскольку в соответствии с данным выше определением (3.1) оно оказывается равным единице.

Будем считать далее, что затухание в линии отсутствует.

Из сравнения выражений для нормированных и ненормированных сопротивлений и проводимостей следует что

(3.6)

Используя эти выражения, приходим к формулам для пересчета нормированных

сопротивлений (проводимостей) в сечение из сечения :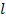

. (3.7)

При использовании соотношений (3.7) необходимо помнить, что 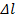положительно при сдвиге от сечения 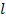в сторону к генератору и отрицательно при сдвиге в сторону нагрузки.

Если под понимать сопротивление нагрузки включенной в линию в сечении 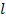=0, тоиз (3.7) можно получить выражения, позволяющие пересчитать сопротивление (проводимость) нагрузки в любое сечение линии передачи, отстоящее на расстояние 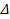l в сторону генератораот сечения входа нагрузки

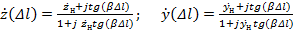(3.8)

при этом 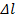положительно и представляет собой расстояние от сечения входа нагрузки до сечения линии, в котором мы хотим определить эквивалентное сопротивление.

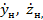
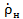в сечении 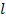=0 связаны соотношениями

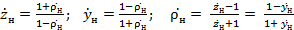(3.9)

Поскольку используемые для трансформации отрезки линий передачи могут отличаться от основной линии передачи в тракте, по размерам поперечного сечения, по конструктивному выполнению, по применяемому типу волн, в схемах замещения это может учитываться введением неединичных безразмерных волновых сопротивлений z _в.

Для этого в (2.14), (2.15) (предыдущая лекция) все величины сопротивлений поделим на z _во, а все проводимости умножим на z _во, где z_во - волновое сопротивление основной линии.

При этом мы получаем соотношения для пересчета сопротивлений и проводимостей, нормированных к волновому сопротивлению z_во основной линии, через отрезок линии длиной с измененным волновым сопротивлением z_вн, так же нормированным к величине z _во:

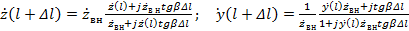. (3.10)

В (3.10) все сопротивления и проводимости являются безразмерными.

В инженерной практике, когда точность определения длин отрезков линий, входящих в проектируемое устройство, не превышает двух значащих цифр, для пересчета сопротивлений (проводимостей) из одного сечения линии передачи в другое, удобно использовать круговую номограмму (диаграмму) полных сопротивлений (проводимостей), называемую также номограммойВольперта или номограммой Вольперта – Смита.

Принцип построения номограммы и примеры ее использования рассматриваются на упражнениях.

Поиск по сайту: