Электромагнитная природа света. Уравнения Максвелла

ПОЛЯРИЗАЦИЯ СВЕТА

Лабораторный практикум по общей физике

Оптика

Издательство «Самарский университет»

Содержание

Часть I

Теоретические основы эксперимента........................... 3

Электромагнитная природа света. Уравнения Максвелла.......... 3

Поперечность световой волны и поляризация света.............. 5

Поляризация при отражении.................................. 11

Прохождение света через анизотропные среды..................13

Поляризаторы.............................................. 17

Интерференция поляризованного света........................ 20

Наведенная анизотропия.................................... 22

Оптическая активность. Вращение плоскости поляризации....... 24

Принцип действия и устройство лазера........................ 28

Библиографический список.................................. 33

Часть II

Экспериментальная часть..................................... 34

Лабораторная работа «ИЗУЧЕНИЕ ПОЛЯРИЗАЦИИ СВЕТА».........34

Лабораторная работа «ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ВРАЩЕНИЯ

И НЕИЗВЕСТНОЙ КОНЦЕНТРАЦИИ САХАРНОГО

РАСТВОРА ПРИ ПОМОЩИ САХАРИМЕТРА СУ-3»......... 41

Лабораторная работа «ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ВРАЩЕНИЯ

И НЕИЗВЕСТНОЙ КОНЦЕНТРАЦИИ САХАРНОГО

РАСТВОРА ПРИ ПОМОЩИ ПОЛЯРИМЕТРА СМ-3»......... 48

Лабораторная работа «ИССЛЕДОВАНИЕ СОСТОЯНИЯ

ПОЛЯРИЗАЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ»................. 55

Поляризация света

Теоретические основы эксперимента

Электромагнитная природа света. Уравнения Максвелла

Вопрос о природе света всегда представлял собой одну из главных проблем оптики. Исследования в этом направлении привели ко многим крупным открытиям в области физики. В 1861 г. шотландец Джеймс Кларк Максвелл вывел систему уравнений для электромагнитного поля, из которой вытекала возможность существования электромагнитных волн, скорость распространения которых определялась величиной электродинамической константы. Определенное Кольраушем и Вебером значение этой постоянной совпало со скоростью света, измеренной Физо. Это позволило Максвеллу предположить, что свет представляет собой электромагнитную волну.

К концу ХIХ века накопилось много фактов, подтверждающих предположение Максвелла. К их числу относятся: опыты Фарадея, в которых наблюдалось влияние магнитного поля на распространение света в веществе; опыты Лебедева, в которых было измерено световое давление; опыты Герца, в которых было доказано существование электромагнитных волн; эксперименты по взаимодействию света с веществом. Дальнейшие исследования показали, что уравнения Максвелла имеют очень глубокое физическое содержание, далеко выходящее за рамки тех фактов и представлений, на основе которых они были получены. Оказалось, что эти уравнения удовлетворяют условию релятивистской инвариантности, хорошо описывают быстропеременное электромагнитное поле, могут быть положены в основу теории излучения электромагнитных волн движущимися зарядами и теории взаимодействия света и вещества.

В удобной для оптики гауссовой системе единиц уравнения Максвелла для электромагнитного поля в среде, где нет объемных зарядов и токов проводимости, имеют вид

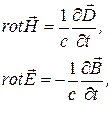
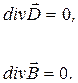(1.1)

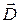Здесь и - напряженность и индукция электрического поля, и 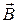- напряженность и индукция магнитного поля, с – электродинамическая постоянная, равная скорости света в вакууме.

Уравнения (1.1) позволяют вывести замкнутые уравнения для полей и , которые называются волновыми уравнениями:

(1.2)

Решения уравнений (1.2) имеют характер распространяющихся волн любой формы. Но наиболее часто в оптике используются модели плоской и сферической гармонических волн, поскольку во многих случаях свойства оптических источников близки к свойствам этих эталонных волн.

Для плоской гармонической волны, находящейся в момент времени t в точке пространства, определяемой радиусом-вектором 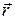, используется тригонометрическая форма записи

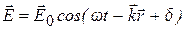, (1.3)

либо комплексная запись

, (1.4)

где - амплитуда волны, ω – круговая частота, 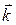- волновой вектор, δ – начальная фаза волны. Величина 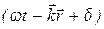называется полной фазой волны.

Гармоническая сферическая волна, расходящаяся от точечного источника, может быть представлена в виде

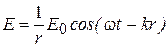. (1.5)

В такой волне напряженности полей зависят только от одной пространственной переменной – модуля радиуса-вектора.

Геометрическое место одинаковых значений фаз называют волновым фронтом. В плоской волне это плоскость, в сферической – сфера.

Поиск по сайту: