МЕТОД БАРЬЕРНЫХ ФУНКЦИЙ

Рассмотрим следующую задачу условной оптимизации:

	,	(2.1)
	,	(2.2)
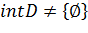	,	(2.3)

Метод состоит в том, что, подобно методу штрафов, задача (2.1-2.2) заменяется задачей безусловной оптимизации:

	,	(2.4)
	,	(2.5)

где – барьерный коэффициент, а – функция, определяемая на основании ограничений и называемая барьерной функцией.

В качестве штрафной функции может быть использована любая функция, обладающая свойствами:

1)	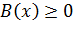,	(2.6)
2)	при	(2.7)

Теорема 2.1. Пусть – некоторая функция, для которой выполняются условия (2.6-2.7) и она непрерывна. Если выполняется хотя бы одно из условий:

1) при ;

2) D ограничено;

тогда при , решение задачи (2.5) будет стремиться к решению задачи (2.1-2.2) и .

Один из вариантов барьерной функции выглядит так:

.

Чем меньше барьерный коэффициент 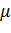, тем точнее решение задачи. Обычно задачу (2.5) решают неоднократно с различными коэффициентами 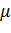. При этом за начальное приближение каждой следующей задачи берётся точное решение предыдущей.

Достоинства метода:

- сведение задачи к задаче безусловной оптимизации;

- решение этой задачи всегда даёт допустимые точки.

Недостатки метода:

- применим только для задач с ограничениями-неравенствами и непустым внутренним множеством;

- для начала решения необходимо найти допустимую точку.

Пример

Задана функция с ограничением . Выполнить один шаг методом барьерных функций.

Решение

1. В качестве начальной точки возьмём , в качестве начального значения барьерного коэффициента и коэффициента его уменьшения – и соответственно, ,

2. Построим новую целевую функцию. Для этого введём в неё барьерную функцию:

;

.

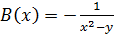Новая целевая функция в таком случае примет следующий вид:

.

3. Найдём точку 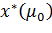методом Ньютона (см. стр. 5):

Находим

;

;

;

;

;

;

.

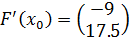Первая итерация метода Ньютона:

;

;

.

Вторая итерация метода Ньютона:

;

;

.

Третья итерация метода Ньютона:

;

;

.

Четвёртая итерация метода Ньютона:

;

;

;

;

.

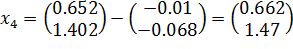4. Т. к. критерий остановки не выполняется, , то , , и переходим к шагу 2. Продолжаем вычисления до тех пор, пока не достигнем заданной точности. Программную реализацию решения данной задачи можно увидеть на рис.2.1.

Поиск по сайту: