 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МЕТОД ПРОЕКЦИИ ГРАДИЕНТА (МЕТОД РОЗЕНА)
Будем рассматривать задачу (2.1)-(2.2) и предполагать в этом случае
 , , 
| (3.1) |
где  .
.
Обозначим через матрицу А набор векторов  :
:
 : :  , где , где 
| (3.2) |
В каждой текущей допустимой точке  под рабочим списком L будем понимать подмножество ограничений, активных в этой точке.
под рабочим списком L будем понимать подмножество ограничений, активных в этой точке.
Все ограничения, которые входят в рабочий список, будут составлять часть ограничений вида (3.2).
Метод проекций градиента состоит в вычислении последовательности точек  , начиная с точки
, начиная с точки  и заканчивая точкой
и заканчивая точкой  так, что все точки являются допустимыми и значения в каждой следующей меньше, чем в предыдущей.
так, что все точки являются допустимыми и значения в каждой следующей меньше, чем в предыдущей.
Подобно тому, как это делалось для задачи безусловной оптимизации
 , ,
| (3.3) |
где  – направление, а
– направление, а  – длина шага.
– длина шага.
Процесс продолжается до тех пор, пока не выполнится теорема Куна-Таккера.
3.1 Выбор направления
В методе проекций градиента направление выбирается следующим образом:
1. Если текущая точка является внутренней области  , то в качестве направления берется антиградиент.
, то в качестве направления берется антиградиент.
2. Если текущая точка является граничной, то в качестве направления берется проекция антиградиента на линейное многообразие, порождаемое множеством активных ограничений, точнее, множеством ограничений, входящих в рабочий список.
Необходимо учитывать два условия:
а) значение функции цели должно уменьшаться;
б) направление не должно выводить из области решений.
Направлением выбирается точка, ограничения которой являются активными в точке  и должны оставаться активными и в следующей точке
и должны оставаться активными и в следующей точке  , то есть при выборе направления должны выполняться следующие условия:
, то есть при выборе направления должны выполняться следующие условия:
 ;
;
 .
.
Отсюда можем определить, что:
 ;
;
 ;
;
 . .
| (3.4) |
Теорема 3.1. Решением задачи поиска минимальной функции  при ограничении
при ограничении  (
( ) является вектор
) является вектор
 , где
, где
 ; ;
| (3.5) | |
 . .
| (3.6) |
 – матрица проектирования, которая проектирует направление аргумента на линейные многообразия порождаемые векторами набора активных ограничений.
– матрица проектирования, которая проектирует направление аргумента на линейные многообразия порождаемые векторами набора активных ограничений.
Для того чтобы убедиться в том, что полученные направления удовлетворяют условию (3.4), достаточно умножить матрицу  на матрицу проектирования:
на матрицу проектирования:
 .
.
3.2 Определение длины шага на каждой итерации.
Вначале найдем для текущей точки  и направления
и направления  максимальную длину шага, при котором мы будем оставаться внутри области допустимых решений. Для этого в новой точке
максимальную длину шага, при котором мы будем оставаться внутри области допустимых решений. Для этого в новой точке  должны выполняться все ограничения вида (2.2). При этом все ограничения рабочего списка в новой точке будут выполняться как строки и равенства, поэтому проверять следует только ограничения, которые не входя в рабочий список.
должны выполняться все ограничения вида (2.2). При этом все ограничения рабочего списка в новой точке будут выполняться как строки и равенства, поэтому проверять следует только ограничения, которые не входя в рабочий список.
 ,
,
 ,
,
 ,
,
 ,
,
 . .
| (3.7) |
Так как точка  , то в этой точке будут выполняться все ограничения вида (2.2).
, то в этой точке будут выполняться все ограничения вида (2.2).
Рассмотрим две ситуации, которые будут возникать при анализе формулы (3.7):
1. 
В этом случае при любом значении  ограничение (3.7) будет выполняться.
ограничение (3.7) будет выполняться.
2. 
 ,
,
 ,
,
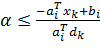 , , 
| (3.8) |
Для того чтобы новая точка была допустимой необходимо, чтобы условие (3.8) выполнялось для всех ограничений. Тогда максимальная длина шага в направлении  может быть получена из формулы:
может быть получена из формулы:
 ,
,
 . .
| (3.9) |
3.3 Критерий оптимальности
Итерационная процедура вида (3.3) будет продолжаться до тех пор, пока в некоторой текущей точке не будут выполняться условия Куна-Таккера, которые будут проверяться только в том случае, если на текущем шаге вектор направления движения 
3.4 Изменение рабочего списка
Добавление ограничений в рабочий список. Если на некоторой итерации длина шага определяется формулой (3.9) совпадает со значением максимальной длины шага, то значит, что еще одно ограничение становится активным и это ограничение добавляется в рабочий список и в матрицу  .
.
Удаление ограничений из рабочего списка. Если на некотором шаге значение вектора  , то в текущей точке проверяется выполнение условий Куна-Таккера, то есть решается следующая задача относительно вектора
, то в текущей точке проверяется выполнение условий Куна-Таккера, то есть решается следующая задача относительно вектора  :
:
 .
.
Если 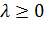 , то это оптимальная точка.
, то это оптимальная точка.
Если  , то выбирается один из них обычно максимальный по модулю и соответствующая строка удаляется из
, то выбирается один из них обычно максимальный по модулю и соответствующая строка удаляется из  .
.
3.5 Общая схема метода проекции градиента
Шаг 0. Определение допустимой точки  .
.
Шаг 1. Построение  .
.
Шаг 2. Если  , то переходим на шаг 6.
, то переходим на шаг 6.
Шаг 3. Определяем  ,
, 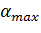 .
.
Шаг 4. Если  , то добавляем ограничение в
, то добавляем ограничение в  .
.
Шаг 5.  ,
, 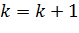 . Переходим на шаг 1.
. Переходим на шаг 1.
Шаг 6. Определение  , решение системы Куна-Таккера.
, решение системы Куна-Таккера.
Шаг 7. Если 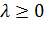 , то
, то  – решение задачи. Остановка алгоритма. Иначе – удаление ограничений из
– решение задачи. Остановка алгоритма. Иначе – удаление ограничений из  и переход на шаг 1.
и переход на шаг 1.
Пример
Задана функция  с ограничениями
с ограничениями
 .
.
Выполнить один шаг методом проекции градиента.
Решение
1. В качестве допустимойточки возьмём
 .
.
2. В данной точке активными являются лишь ограничения неотрицательности параметров 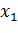 и
и  . Тогда
. Тогда

и в соответствие с (3.6) имеем:
 .
.
Так как  – нулевая матрица, то из (3.5) видно, что
– нулевая матрица, то из (3.5) видно, что  .
.
3. Определим λ как решение системы Куна-Таккера:
 ;
;
 ;
;
 .
.
Удалим из матрицы  ту строку, индексы которой соответствует максимальное по модулю значение
ту строку, индексы которой соответствует максимальное по модулю значение 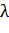 .
.
Тогда получим новую матрицу  , для которой
, для которой
 ,
,
 .
.
Имеем 
4. Для определения 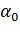 найдем минимум функции
найдем минимум функции 

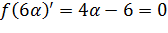
 .
.
Для определения максимальной длины шага 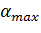 рассчитаем
рассчитаем  , где
, где  – ограничения, не входящие в рабочий список:
– ограничения, не входящие в рабочий список:
 ;
;
 ;
;
и выберем минимальное из двух значений:
 ;
;
 .
.
Получили, что  .
.
5. Переходим на шаг 1 для новой допустимой точки:
 .
.
4 МЕТОД ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
(МЕТОД ЗОЙТЕНДЕЙКА)
Для каждой допустимой точки  в
в  может существовать множество различных допустимых направлений. Сущность методов допустимых направлений сводится к следующему: поиск начинается в допустимой точке пространства решений и реализуется по траектории, обеспечивающей улучшение значений целевой функции и вместе с тем никогда не выходящей за пределы допустимой области. В этом смысле предложенный Розеном метод проекции градиента представляет собой одну из модификаций метода допустимых направлений. Однако необходимо обратить внимание на следующее: проекция градиента
может существовать множество различных допустимых направлений. Сущность методов допустимых направлений сводится к следующему: поиск начинается в допустимой точке пространства решений и реализуется по траектории, обеспечивающей улучшение значений целевой функции и вместе с тем никогда не выходящей за пределы допустимой области. В этом смысле предложенный Розеном метод проекции градиента представляет собой одну из модификаций метода допустимых направлений. Однако необходимо обратить внимание на следующее: проекция градиента 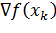 на подмножество ограничений, содержащее
на подмножество ограничений, содержащее  , задает направление поиска, соответствующее направлению наискорейшего спуска для целевой функции, тогда как в методе Зойтендейка используется метрика, определяемая соотношением
, задает направление поиска, соответствующее направлению наискорейшего спуска для целевой функции, тогда как в методе Зойтендейка используется метрика, определяемая соотношением
 .
.
Данная метрика приводит к тому, что в качестве допустимого выбирается направление, которое обеспечивает наибольшую минимизирующую поправку к значению целевой функции без нарушения какого-либо из ограничений.
Метод Зойтендейка позволяет оперировать как с линейными, так и с нелинейными ограничениями; однако с его помощью не удается решать задачи с ограничениями в виде равенств.
Рассмотрим задачу вида (2.1)-(2.2). Линеаризация фигурирующих в этой задаче функций путем их разложения в ряд Тейлора в окрестности точки  приводит к следующей задаче:
приводит к следующей задаче:

при ограничениях
 . .
| (4.1) |
Процедура Зойтендейка устанавливает наиболее благоприятные из возможных направлений поиска при отправной точке  путем решения некоторой подзадачи, структура которой указана ниже.
путем решения некоторой подзадачи, структура которой указана ниже.
Перемещение из точки  в точку
в точку  задаетсясоотношением
задаетсясоотношением
 .
.
Подстановка в задаче (4.1) вместо вектора  его текущего значения
его текущего значения  приводит к задаче
приводит к задаче

при ограничениях
 . .
| (4.2) |
Поскольку  и
и  являются константами, то необходимые и достаточные условия реализации перемещения из точки
являются константами, то необходимые и достаточные условия реализации перемещения из точки  в точку
в точку  в связи с решением задачи (4.2) имеют следующий вид:
в связи с решением задачи (4.2) имеют следующий вид:

| (4.3) | |
и 
| (4.4) |
Любой вектор  , удовлетворяющий неравенствам (4.3) и (4.4), одновременно является вектором допустимого направления.
, удовлетворяющий неравенствам (4.3) и (4.4), одновременно является вектором допустимого направления.
Метод Зойтендейка выделяет допустимое направление, обеспечивающее получение наибольшей минимизирующей поправки к значению целевой функции  на шаге от точки
на шаге от точки  к точке
к точке  путём решения следующей задачи линейного программирования:
путём решения следующей задачи линейного программирования:

| (4.5) |
при условиях

Решая задачу (4.5), определяются составляющие вектора допустимого направления, вдоль которого следует перемещаться из точки  в точку
в точку  .
.
Алгоритм метода возможных направлений
Шаг 1. Пусть  – некоторая допустимая точка задачи (2.1)-(2.2) с ограничениями в виде неравенств.
– некоторая допустимая точка задачи (2.1)-(2.2) с ограничениями в виде неравенств.
Шаг 2. Вычисляются градиенты функции  и
и  в точке
в точке  , и решается задача (4.5), в результате чего находится допустимое направление
, и решается задача (4.5), в результате чего находится допустимое направление  . Решение задачи (4.5) находится с помощью любого из алгоритмов линейного программирования.
. Решение задачи (4.5) находится с помощью любого из алгоритмов линейного программирования.
Шаг 3. Если  , то определяется максимальная длина шага
, то определяется максимальная длина шага 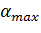 , осуществляемого в направлении
, осуществляемого в направлении  без выхода за пределы допустимой области задачи (1.1)-(1.2):
без выхода за пределы допустимой области задачи (1.1)-(1.2):
 .
.
Затем определяется  :
:
 .
.
Новая точка определяется как  . Теперь возвращаются к шагу 2 с тем, чтобы начать оптимизационный поиск на (k + 1)-м этапе вычислительного процесса.
. Теперь возвращаются к шагу 2 с тем, чтобы начать оптимизационный поиск на (k + 1)-м этапе вычислительного процесса.
Шаг 4. Если  , поиск решений заканчивается, так как дальнейшее уменьшение значения
, поиск решений заканчивается, так как дальнейшее уменьшение значения  не представляется возможным.
не представляется возможным.
Пример.
Задана функция 
с ограничениями
 .
.
Выполнить один шаг методом возможных направлений.
Решение.
1. В качестве допустимойточки возьмём
 .
.
2. Вычислим градиенты функции  и
и  в точке
в точке  :
:
 ,
,
 .
.
В данной точке активными являются лишь ограничения неотрицательности параметров 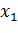 и
и  . Тогда
. Тогда
 .
.
Решив задачу 
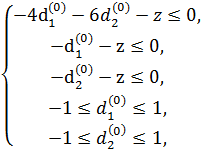
симплекс-методом, получаем  .
.
Для определения максимальной длины шага 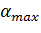 рассчитаем
рассчитаем  , где
, где  – ограничения, не входящие в рабочий список:
– ограничения, не входящие в рабочий список:
 ,
,

и выберем минимальное из двух значений:
 ,
,
 .
.
Получили, что  . Тогда
. Тогда
 .
.
Переходим на шаг 2 для новой допустимой точки:
 .
.
Программную реализацию решения данной задачи можно увидеть на рис.4.1.
Пример выполнения задания для курсового проекта
Постановка задачи: разместить без взаимных пересечений n кругов различных радиусов в полубесконечной полосе так, чтобы длина занятой её части была минимальной.
1 Построение математической модели
1.1 Обозначенияинеформальнаяпостановка
Введём необходимыеобозначения. Обозначимполубесконечную полосу буквой S. Количество кругов обозначим n, i-й круг – Ti, радиус i-го круга – ri,  . Примем за полюс круга его центр. Границей размещения назовём отрезок на полосе S, после которого не расположено ни одного круга. Расстояние от начала полосы до этого отрезка обозначим Z (рис.1.1).
. Примем за полюс круга его центр. Границей размещения назовём отрезок на полосе S, после которого не расположено ни одного круга. Расстояние от начала полосы до этого отрезка обозначим Z (рис.1.1).

Рисунок 1.1 – Геометрическое представление задачи
Параметрами размещения i-го круга являются координаты его центра (xi, yi). Так как они имеют определенный физический смысл, то их можно считать составляющими вектора Хi.
Задачей является размещение набора кругов так, чтобы длина занимаемой части полосы была минимальной.
Математическая модель содержит область допустимых решений и функцию цели. Обозначим область допустимых решений буквой D.
1.2 Область допустимых решений задачи
Если существует набор векторов Хi,  , такой, который попадает в область допустимых значений D, то задача имеет решение и данный набор векторов является одним из решений.
, такой, который попадает в область допустимых значений D, то задача имеет решение и данный набор векторов является одним из решений.
Область D описывается условиями:
а) круги должны принадлежать полосе (рис. 1.2):
Ti (Хi)  S,
S,  . (1.1)
. (1.1)

Рисунок 1.2 – Геометрическое представление условия принадлежности кругов полосе
б) круги не должны пересекаться между собой (рис. 1.3):
int Ti(Хi) ∩ int Tj(Хj) = 0, 
 ;
;  . (1.2)
. (1.2)
Для формализации условий не пересечения был разработан аппарат Ф-функции [14].
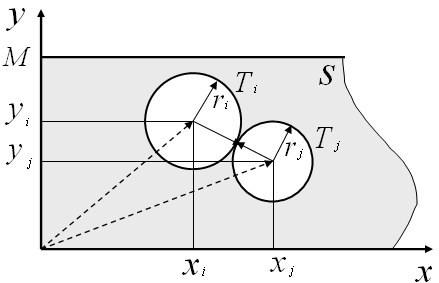
Рисунок 1.3 – Геометрическое представление условия не пересечения пары кругов
1.3 Использование Ф-функций
Ф-функции вводят для каждой пары Ti, Tj размещаемых объектов. При определении и описании их свойств будем учитывать особенности нашей задачи. Зависимость объекта  от значения вектора переменных соответствующей геометрической информации будем выражать в виде –
от значения вектора переменных соответствующей геометрической информации будем выражать в виде –  . Для нашей задачи
. Для нашей задачи  .
.
Любая, всюдуопределенная и непрерывная функция в  , обладающая следующим характеристическим свойством:
, обладающая следующим характеристическим свойством:
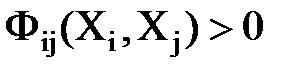 , если
, если  ;
;
 , если
, если  ,
,
 ;
;
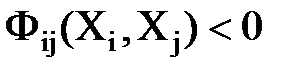 , если
, если  ,
,
называется Ф-функцией [14].
Таким образом, характеристическое свойство  – функции позволяет говорить о пересечении, не пересечении и касании соответствующих объектов. Причем условия непересечения для пары размещаемых объектов выполняется тогда и только тогда, когда размещаемые объекты принадлежат области неотрицательных значений соответствующей Ф-функции.
– функции позволяет говорить о пересечении, не пересечении и касании соответствующих объектов. Причем условия непересечения для пары размещаемых объектов выполняется тогда и только тогда, когда размещаемые объекты принадлежат области неотрицательных значений соответствующей Ф-функции.
Условия (1.1, 1.2) можно записать в виде Ф-функций. Условие (1.1) эквивалентно выполнению неравенства
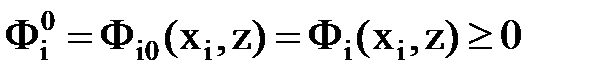 ,
,
а условие (1.2) соответствует выполнению неравенства

Таким образом, область допустимых решений задачи  описывается с помощью Ф-функций так:
описывается с помощью Ф-функций так:
 (1.3)
(1.3)
Представим область допустимых решений задачи (1.3) в аналитическом виде.
1.4 Описание Фi0 – функции
Представим условие принадлежности кругов полосе в аналитическом виде. Графическое представление показано на рис. 1.2, математическое представление выражено условием Ti (Xi)  S, которое эквивалентно системе неравенств (1.4).
S, которое эквивалентно системе неравенств (1.4).
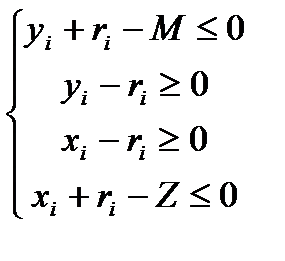 (1.4)
(1.4)
Неравенство  представляет собой условие непересечения кругов верхней границы, неравенство
представляет собой условие непересечения кругов верхней границы, неравенство  – нижней, неравенство
– нижней, неравенство  – левой, неравенство
– левой, неравенство  - правой.
- правой.
Система неравенств (1.4) эквивалентна уравнению 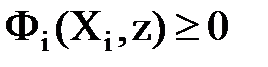 системы (1.3)
системы (1.3)
Систему 1.4 для удобства запишем в виде:
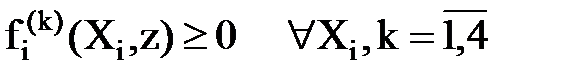 (1.5)
(1.5)
1.5 Описание Фij – функции
Представим условие не пересечения кругов в аналитическом виде. Графическое представление показано на рис.1.3, математическое представление для каждой пары кругов выражено условием  , которое эквивалентно неравенству (1.6).
, которое эквивалентно неравенству (1.6).
 , где
, где  (1.6)
(1.6)
Неравенство (1.5) эквивалентно уравнению  системы (1.3)
системы (1.3)
1.6 Математическая модель
Функция цели имеет вид:  ,
,
Или 

где 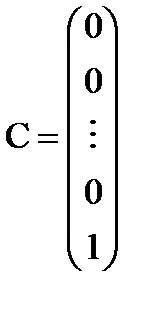 ,
,  ,
,  ,
,
xi, yi – координаты полюса i-го круга.
Исходя из (1.4 – 1.6) область D описывается:

2 Особенности реализации метода локального минимума с использованием метода проекции градиента
2.1 Построение начального приближения
Каждый круг размещается таким образом, чтобы он касался нижней границы полосы и предыдущего круга (рис 2.1).
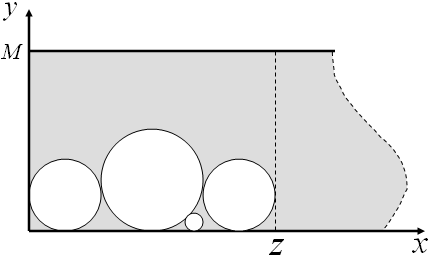
Рисунок 2.1 – Первое размещение кругов
Координаты первого круга будут:  где
где  радиус первого круга (рис. 2.2).
радиус первого круга (рис. 2.2).

Рисунок 2.2 – Координаты кругов первого размещения
Чтобы получить значение координата второго круга (рис. 3.3) обратимся к следующим формулам:


Рисунок 2.3 – Определение координат второго круга
Координаты второго круга будут:

и т.д.
2.2 Вычисления длины шага для линейных ограничений
Произведем вычисления длины шага для линейного ограничения. Для такого вида ограничений будет справедливо следующее:
 .
.
Если  – исходная точка, то
– исходная точка, то
 ,
,
 ,
,
 ,
,  .
.
 - значение в предыдущей точке
- значение в предыдущей точке  , это допустимая точка.
, это допустимая точка.
Следовательно  .
.
Если  , то в точке
, то в точке  ограничения
ограничения  будет выполняться при любом
будет выполняться при любом  .
.
Пусть  , тогда
, тогда 
 ,
,
 .
.
Номер k - того шага:


2.3 Вычисление длины шага для нелинейных ограничений
Произведем вычисления длины шага для нелинейного ограничений. Для такого вида ограничений будет справедливо следующее (рис. 2.4):
Y – Вектор направление;
X – Исходная точка.

Рисунок 2.4 – Размещение кругов
Произведем выбор вектора направления:

 ,
,
где
 ,
,  .
.
Кроме того, справедливо:

Приводим к виду:  , где
, где  .
.
Находим решения  и
и  :
:
1) При  и длина шага min
и длина шага min 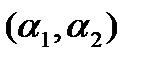 (рис 2.5);
(рис 2.5);

Рисунок 2.5 – Представление нахождения длины шага при 
2) При  длина шага
длина шага  (рис 2.6);
(рис 2.6);

Рисунок 2.6 – Представление не пресекающих кругов при 
3) При 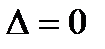 длина шага
длина шага  (рис 2.7);
(рис 2.7);

Рисунок 2.7 – Когда круг пройдет через точки касания
2.4 Удаление нелинейных ограничений из матрицы активных ограничений
Если нелинейное ограничение перестает быть активным (рис. 2.8), то из матрицы активных ограничений удаляем соответствующее ему линейное ограничение (рис. 2.9).
После изменения точки размещения, удаляем из матрицы активных ограничений, те которые перестали быть активными.

Рисунок 2.8 – Движение кругов за направлением

Рисунок 2.9 – Удаление соответствующего не активного ограничения
2.5 Иллюстрация процесса движения
Покажем как размещается каждый круг с первого до конечного размещения и как он двигается, и при этом получаем по каждому шагу новое оптимальное решение. Получим допустимое начальное размещения для трех кругов (рис. 2.10, а-е).

а

б

в

г

д

е
Рисунок 2.10 – Допустимое начальное до конечного размещения для трех кругов: а – первый шаг; б – второй шаг; в – пятый шаг; г – шестой шаг;
д – девятый шаг; е – десятый шаг
3 Описание программного продукта
На основе выбранных алгоритмов в математическом пакете MatLab разработан и реализован программный продукт (ПП), решающий поставленную задачу размещения плоских геометрических объектов на полубесконечной полосе. Данный ПП предназначен для размещения окружностей с помощью метода проекционного градиента.
Исходными данными задачи является радиусы, размещаемых кругов и ширина полосы. В результате работы программы пользователь получает возможность наглядно увидеть лучшее размещение в графическом окне программного продукта.
Работа с программой начинается с запуска математического пакета MatLab. Затем открываем м-файл с основной программой. Для этого выбирается пункт главного меню Файл à Открыть. Появляется программный код (рис. 3.1).
В данном файле задаются следующие параметры: ширина полосы и набор радиусов. Кроме того, можно генерировать случайные радиусы окружностей.
После того как заданы данные для размещения, производим запуск программного продукта с помощью Run, и через некоторое время появится графическое окно размещения окружностей на полубесконечной полосе, которое показано на рис. 3.2.

Рисунок 3.1 – Загрузка м-файла с программным кодом

Рисунок 3.2 – Графическое окно программы после выполнения размещения для 15 случайных окружностей
Как видно из рис. 3.2 длина начального размещения – 116.16, ширина полосы - 40, а минимальная длина – 35.96.
Приведем на рис. 3.3 пример размещения для 50 случайных окружностей и ширине полосы – 30.

Рисунок 3.3 – Графическое окно программы после выполнения размещения для 50 случайных окружностей и ширине полосы равной 30
Список использованных источников
1. А.Фиакко, Г.Мак-Кормик «Нелинейное программирование. Методы последовательной безусловной минимизации», М.:Издательство «Мир», 1972. – 241с.
2. Мину М. Математическое программирование. Теория и алгоритмы: Пер. с фр. и предисловие А.И.Штерна. – М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 488 с.
3. Базара М., Шетти К.Нелинейное программирование. Теория и алгоритмы: Пер. с англ. – М.: Издательство «Мир», 1982. – 583с.
4. Химмельблау Д. «Прикладное нелинейное программирование», М.: Издательство «Мир», 1975. – 536с.
5. А.В.Аттетков,С.В.Галкин,В.С.Зарубин. Методы оптимизации: Учеб.для вузов /В.С.Зарубина, А.П.Крищенко. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. – 440 с. (Сер. Математика в техническом университете; Вып. XIV).
6. Харчистов Б.Ф.Методы оптимизации: Учебное пособие. – Таганрог: Изд-во ТРТУ, 2004. – 140с.
7. http://iasa.org.ua/ru/forstudent/materials.html - учебный материал по дисциплине «Исследование операций» на сайте факультета второго высшего и последипломного образования ННК «ИПСА» НТУ «КПИ»
8. Барсов С.С., Храпов П.В., Чуев В.Ю. Численные метода поиска экстремума: Методические указания к выполнению лабораторных работ по курсу «Численные методы». – М.: Изд-во МГТУ, 1990. – 35с., ил.
9. http://mmedia0.cc.rsu.ru/pls/rsuweb/umr.umr_download?p_umr_id=44985 – Сантылова Л.И., Гусаков С.В., Землянухина Л.Н. «Вариационное исчисление и методы оптимизации»: Метод.указания для студентов специальности «Прикладная математика и информатика» - Ростов-на-Дону: мех.-мат. фак. ЮФУ, 2010
Поиск по сайту: