 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Виды задач линейного программирования
Наиболее распространенный тип задач – задача оптимального использования ресурсов. Пусть некоторая производственная единица (цех, предприятие, объединение и т.д.), исходя из конъюнктуры рынка, технических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции, известных под номерами j.
При выпуске продукции предприятие ограничено имеющимися ресурсами, количество которых обозначим m, а вектор ресурсов В = (b1, b2,..., bт). Известны также технологические коэффициенты aij, которые показывают норму расхода i -го ресурса на производство единицы j -ой продукции. Эффективность выпуска единицы j -и продукции характеризуется прибылью pj.
Требуется определить план выпуска продукции Х=(х1, х2,..., xп), максимизирующий прибыль предприятия при заданных ресурсах.
Целевая функция выглядит следующим образом
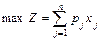 , (1)
, (1)
при ограничениях 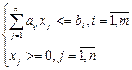 . (2)
. (2)
Часто ассортимент продукции устанавливается вышестоящей организацией, т. е. его объемы должны быть заключены в некоторых границах Dнj и Dвj: тогда задается следующее ограничение:  (3)
(3)
Модель задачи оптимального использования ресурсов лежит в основе моделей оптимизации годовой производственной программы предприятия. В модель включаются ограничения по фонду времени работы оборудования.
Сохраняя прежние обозначения, запишем через αj и сj соответственно отпускную цену и затраты на единицу j-й продукции. В качестве критерия оптимальности могут быть приняты:
1) максимум прибыли 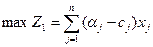
2) минимум затрат на производство 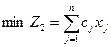
3) максимум выпуска в стоимостном выражении (выручки от реализации продукции)

4. Линейное программирование. Виды задач линейного программирования: оптимального использования ресурсов и размещения заказов или загрузки взаимозаменяемых групп оборудования.
Линейное программирование – это раздел матпрограммирования, применяемый при разработке методов нахождения экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные.
По типу решаемых задач методы ЛП разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП).
Главная особенность задач линейного программирования заключается в том, что экстремум целевой функции находится на границе области допустимых решений.
 |
Рисунок 1 – Экстремум целевой функции
Математическая модель ЗЛП записывается следующим образом:
max (или min) Z=z(X), (1) X Î D.
ОДР может быть представлена системой линейных уравнений или неравенств.
Вектор Х=(х1, х2,.... x п) является вектором управления или управляющим воздействия.
Допустимый план Х, при котором критерий оптимальности Z=z(X) достигаетэкстремального значения, называется оптимальным и обозначается через X*, экстремальное значение целевой функции — через Z*=z(X*).
Наиболее распространенный тип задач – задача оптимального использования ресурсов. Пусть некоторая производственная единица (цех, предприятие, объединение и т.д.), исходя из конъюнктуры рынка, технических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции, известных под номерами j.
При выпуске продукции предприятие ограничено имеющимися ресурсами, количество которых обозначим m, а вектор ресурсов В = (b1, b2,..., bт). Известны также технологические коэффициенты aij, которые показывают норму расхода i -го ресурса на производство единицы j -ой продукции. Эффективность выпуска единицы j -и продукции характеризуется прибылью pj.
Требуется определить план выпуска продукции Х=(х1, х2,..., xп), максимизирующий прибыль предприятия при заданных ресурсах.
Целевая функция выглядит следующим образом
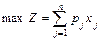 , (1)
, (1)
при ограничениях 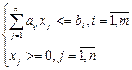 . (2)
. (2)
Часто ассортимент продукции устанавливается вышестоящей организацией, т. е. его объемы должны быть заключены в некоторых границах Dнj и Dвj: тогда задается следующее ограничение:  (3)
(3)
Задача о размещении заказов или загрузке взаимозаменяемых групп оборудования. Речь идет о распределения заказов между m (i=1,…, m) предприятиями (цехами, станками, исполнителями) с различными производственными и технологическими характеристиками, но взаимозаменяемыми в смысле выполнения заказов. Требуется составить такой план размещения заказов, при котором задание было бы выполнено, а показатель эффективности достигал экстремального значения.
Сформулируем задачу математически. Пусть на т однородных группах оборудования нужно изготовить п видов продукции. План выпуска каждого вида продукции на определенный период задан набором хj (j = 1,2, … п). Мощность каждого вида оборудования ограничена и равна bi. Известна технологическая матрица A=||aij||, где aij— число единиц j- ой продукции, выпускаемой в единицу времени на i -м оборудовании. Матрица С – матрица затрат, где cij— затраты, связанные с выпуском единицы j-й продукции на i-м оборудовании. Х — вектор объема выпускаемой продукции.
Модель задачи примет следующий вид:
целевая функция — минимизация расходов на реализацию всех заказов
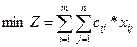 при ограничениях:
при ограничениях:
а) по мощности оборудования 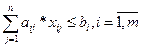 ;
;
б) на выпуск продукции 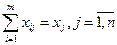 ;
;
в) условие неотрицательности 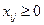 .
.
Данную задачу называют распределительной или задачей распределения.
Если по некоторым видам продукции допускается превышение плана, то ограничение (б) примет вид 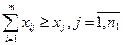 .
.
В качестве целевой прибыли также можно принять:
а) максимум прибыли  ;
;
б) минимум затрат станочного времени  .
.
Т.к. любая модель содержит упрощающие предпосылки, для корректного применения полученных результатов необходимо четкое понимание сути этих упрощений, что, в конечном счете, и позволяет сделать вывод об их допустимости или недопустимости. Наиболее существенным упрощением в рассмотренных моделях является предположение о прямопропорциональной (линейной) зависимости между объемами расхода ресурсов и объемами производства, которая задается с помощью норм затрат aij.
5. Формы записи задач линейного программирования.
Существует 3 формы записи ЗЛП:
1) в виде функций
max(или min)Z= 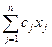 , max(или min)Z=
, max(или min)Z=  ,
,
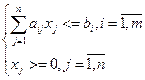
 .
.
2) векторная форма
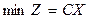 (скалярное произведение векторов)
(скалярное произведение векторов)
при ограничениях A1х1+A2х2+..+Anxn = B
x>=0.
Где векторы С = (С1, С2.. Сn), Х = (Х1, Х2.. Хn),  и
и 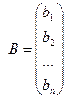 .
.
3) матричная форма
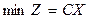
при ограничениях AХ = B
X>=0,
где С = (с1, с2,…сn), 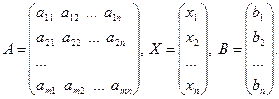
6. Каноническая форма задач линейного программирования.
Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные xj налагаются условия неотрицательности, то она называется задачей линейного программирования в канонической форме или канонической задачей линейного программирования (КЗЛП).

при ограничениях
 .
.
Для того чтобы перейти от ЗЛП к КЛЗП, необходимо перейти от ограничений неравенств к ограничениям равенствам и заменить переменные, которые не подчиняются условиям неотрицательности.
Правила приведения ЗЛП к каноническому виду:
1) если в ограничениях правая часть отрицательная, то следует умножить это ограничение на -1;
2) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;
3) если некоторая переменная xk не имеет ограничений по знаку, то она заменяется в целевой функции и во всех ограничениях разностью между двумя новыми неотрицательными переменными: xk=x*k - xl, где l - сводный индекс, x*k>=, xl>=0.
7. Симплексный метод: построение начального опорного плана, предпочтительный вид.
Пусть поставлена задача: найти минимальное значение целевой функции
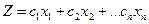
при канонических ограничениях:

 .
.
Ограничение имеет предпочтительный вид, если при неотрицательной правой части (bi ≥ 0) левая содержит переменную, входящую в данное уравнение с коэффициентом, равным единице, а в остальные ограничения-равенства с коэффициентом, равным нулю.
Приравнивание предпочтительных переменных к правым частям дает базисное решение, то они называются базисными. Все остальные переменные, значения которых приравниваем к нулю, называются свободными.
При приведении системы ограничений к предпочтительному виду возможны два случая.
1) пусть задана система: 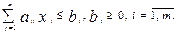
Добавив к левым частям дополнительные переменные 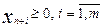 , получим расширенную задачу эквивалентную исходной.
, получим расширенную задачу эквивалентную исходной.
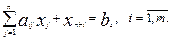
Но в расширенной задаче система ограничений имеет предпочтительный вид, следовательно, начальный опорный план:  .
.
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю: 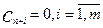
2) задана систему ограничений: 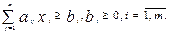
Вычитая из левых частей дополнительные переменные 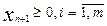 , получим расширенную задачу. Однако система ограничений не имеет предпочтительного вида, так как дополнительные переменные входят в левую часть с коэффициентами, равными минус единице. Поэтому план
, получим расширенную задачу. Однако система ограничений не имеет предпочтительного вида, так как дополнительные переменные входят в левую часть с коэффициентами, равными минус единице. Поэтому план  недопустим. В этом случае вводят так называемый искусственный базис. К левым частям системы ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные Wi. В целевую функцию Wi вводят с коэффициентом, равным (+М) в случае решения задачи на min, и с коэффициентом (-М) – на max, где М – большое положительное число. Полученная задача называется М-задачей.
недопустим. В этом случае вводят так называемый искусственный базис. К левым частям системы ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные Wi. В целевую функцию Wi вводят с коэффициентом, равным (+М) в случае решения задачи на min, и с коэффициентом (-М) – на max, где М – большое положительное число. Полученная задача называется М-задачей.
М-задача формируется и в случае, когда ЗЛП задана в канонической форме, но не имеет предпочтительного вида.
Пусть дана задача линейного программирования:
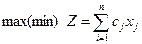

Если ни одно из ограничений не имеет предпочтительного вида, то М-задача запишется:
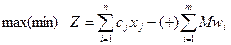
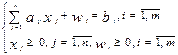
Где знак (-) в относится к задаче на max. Начальный опорный план задачи: 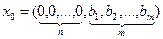 .
.
Если в оптимальном плане М-задачи  все искусственные переменные равны нулю, то план
все искусственные переменные равны нулю, то план 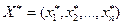 оптимален для исходной задачи. Если же хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна.
оптимален для исходной задачи. Если же хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна.
8. Симплексный метод: симплексные таблицы, признак оптимальности опорного плана.
Для решения задач обычно условия заносят в таблицу, которая называется симплексной. Перед занесением систему ограничений приводят к предпочтительному виду.
Пример. 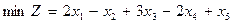
при ограничениях
 .
.
Система ограничений данной задачи имеет предпочтительный вид. Составим симплексную таблицу.
| Б.п. | СБ | А0 | х1 | х2 | х3 | х4 | х5 |
| -1 | -2 | ||||||
| х2 | -1 | 3/2 | 1/2 | 1/2 | |||
| х4 | -2 | ||||||
| х1 | 1/2 | -1/2 | 1/2 | ||||
| Целевая функция | -9/2 | -13/2 | -1/2 |
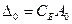 ;
;  .
.


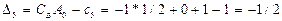
Находим начальный опорный план 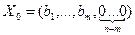 ,
, 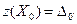
Обозначим через Б множество базисных переменных, через В - множество свободных переменных. Очевидно, при 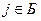 ,
,  . Значения
. Значения 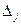 ,
,  называются оценками свободных переменных.
называются оценками свободных переменных.
Признак оптимальности опорного плана:
1) Опорный план 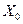 доставляет целевой функции минимальное значение
доставляет целевой функции минимальное значение  , если для него все оценки свободных переменных неположительны.
, если для него все оценки свободных переменных неположительны.
2) Опорный план 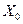 доставляет целевой функции максимальное значение
доставляет целевой функции максимальное значение 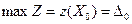 , если все оценки свободных переменных неотрицательны.
, если все оценки свободных переменных неотрицательны.
Строка функции цели называется Z-строкой или индексной строкой. Начальный опорный план Х0=(1/2;3/2;0;2;0) и Z(Х0)=-9/2. Т.к. все оценки индексной строки неположительны, то план Х0 - оптимален.
9. Симплексный метод: переход к нехудшему опорному плану, симплексные преобразования.
Рассмотрим задачу 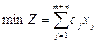 ,
,
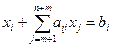 ,
, 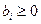 ,
, 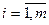 ,
,
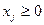 ,
, 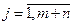 .
.
Начальный опорный план 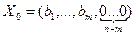 ,
,  . Если все оценки свободныхпеременных
. Если все оценки свободныхпеременных  , то план Х0 - оптимальный. Если существуют положительные оценки свободных переменных, то столбец, которому соответствует наибольшее значение ∆j называется разрешающим. Обозначим его номер jo, а величину xjo введем в базис.
, то план Х0 - оптимальный. Если существуют положительные оценки свободных переменных, то столбец, которому соответствует наибольшее значение ∆j называется разрешающим. Обозначим его номер jo, а величину xjo введем в базис.
Т.к. ∆jо > 0, то, не изменяя нулевых значений всех свободных переменных, можно уменьшить функцию Z за счет увеличения xjo.
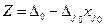 .
.
Чтобы перейти к новому опорному плану из базиса нужно вывести одну из переменных.
Значение xjo нужно увеличить так, чтобы ни одно из значений базисных переменных xi не было отрицательным. Т.е.
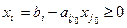 .
. 
Возможны два случая.
1) Все элементы разрешающего столбца jo неположительны, т.е. aijo ≤ 0. Если при решении задачи на min (max) в индексной строке имеются положительные (отрицательные) оценки свободных переменных, а в столбце переменной xjo нет ни одного положительного элемента, то целевая функция не ограниченна снизу (сверху) на множестве допустимых планов задачи.
2) Если среди элементов разрешающего столбца имеются положительные, то xjo можно увеличивать до тех пор, пока не нарушается система неравенств:
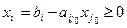 .
. 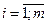 .
.
Отсюда получаем 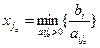 .
.
Пусть данное выражение выполняется при i=io, тогда  .
.
Если условие выполняется при нескольких i, то в качестве io можно выбрать любое. Строку io называют разрешающей, элемент 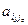 - разрешающим.
- разрешающим.
Новое значение целевой функции: 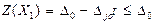 .
.
В результате преобразований целевая функция уменьшилась. Теперь новую базисную переменную нужно выразить через свободные и подставить в систему ограничений и целевую функцию. Причем старая базисная переменная становится свободной.
Правила симплексного преобразования:
1) В индексной строке симплекс-таблицы найти наибольший положительный (или отрицательный) элемент. Столбец соответствующий этому элементу - разрешающий.
2) Вычислить отношение свободных членов уравнения к положительным элементам разрешающего столбца. Данное отношение называется симплекс-отношением. Найти наименьшее из симплекс-отношений, оно соответствует разрешающей строке.
3) На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент 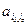 . Если имеется несколько одинаковых по величине симплекс-отношений, то выбирают любое из них.
. Если имеется несколько одинаковых по величине симплекс-отношений, то выбирают любое из них.
4) Неизвестные элементы, соответствующие разрешающим столбцу и строке, меняются местами.
5) Переход к следующей таблице. Элементы разрешающей строки новой таблицы будут равны  и
и 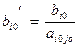 .
.
6) Элементы разрешающего столбца равны нулю, за исключением  , т.к. xjo - базисная величина.
, т.к. xjo - базисная величина.
7) Все остальные элементы находятся по формулам  и
и 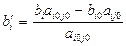 . Для нахождения элементов в исходной таблице выделяется прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий и искомый элемент новой таблицы, называется главной, а другая - побочной. Из произведения угловых элементов главной диагонали вычитается произведение угловых элементов побочной диагонали и полученное число делят на разрешающий элемент. Это правило прямоугольника.
. Для нахождения элементов в исходной таблице выделяется прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий и искомый элемент новой таблицы, называется главной, а другая - побочной. Из произведения угловых элементов главной диагонали вычитается произведение угловых элементов побочной диагонали и полученное число делят на разрешающий элемент. Это правило прямоугольника.
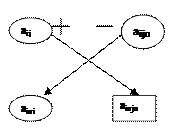
8) вычисляем элементы индексной строки  и
и  . Для контроля вычислений можно вычислить
. Для контроля вычислений можно вычислить  и
и 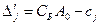 .
.
9) алгоритм продолжается до тех пор, пока не будет достигнуто условие оптимальности.
а) Опорный план 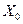 доставляет целевой функции минимальное значение
доставляет целевой функции минимальное значение 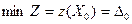 , если для него все оценки свободных переменных неположительные.
, если для него все оценки свободных переменных неположительные.
б) Опорный план 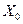 доставляет целевой функции максимальное значение
доставляет целевой функции максимальное значение 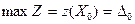 , если все оценки свободных переменных неотрицательны.
, если все оценки свободных переменных неотрицательны.
10. Понятие двойственности в задачах линейного программирования. Правила построения двойственных задач (симметричных и несимметричных).
Понятие двойственности рассмотрим на примере задачи оптимального использования сырья. Пусть на предприятии решили рационально использовать отходы основного производства. В плановом периоде появились отходы ресурсов m видов в объемах bi единиц соответственно (i =1;m). Из этих отходов, учитывая специализацию предприятия можно наладить выпуск n видов основной продукции.
Введем обозначения:
ai j – норма расхода i -го ресурса на производство j -ой продукции;
cj – цена реализации j -ой продукции;
xj – объем выпуска j -ой продукции, обеспечивающей предприятию максимум прибыли.
Математическая модель задачи:

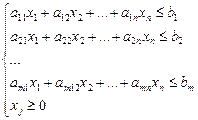 .
.
Оценки должны быть установлены исходя из следующих требований, отражающие несовпадающие интересы предприятия и организации:
1) общую стоимость отходов производства покупающая организация стремиться минимизировать;
2) предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку не меньшую той, что могло бы получить организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП:
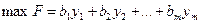 – это требование покупающей организации.
– это требование покупающей организации.
Требования предприятия, реализующего отходы, можно сформулировать в виде системы ограничений. Предприятие откажется от выпуска каждой единицы продукции первого вида, если
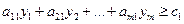 .
.
Левая часть неравенства выражает стоимость ресурсов, идущих на производство единицы продукции первого вида; правая – цену продукции.
Аналогичные рассуждения можно провести относительно каждого вида продукции, в результате получим следующую систему ограничений:
 .
.
Переменные yi называются двойственными оценками или объективно обусловленными оценками. В зарубежной литературе их называют теневыми ценами.
Первая и вторая задачи называются парой взаимно двойственных ЗЛП. Т.к. эти задачи записаны в симметричной форме, то их принято называть парой симметричных двойственных задач.
В общем виде пара симметричных двойственных задач имеет следующий вид:
Прямая задача: Двойственная задача:
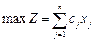
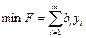
 ;
; 
Если в качестве прямой принять задачу об определении оптимальных оценок на ресурсы, то в двойственной к ней будет задача об определении оптимального плана выпуска продукции.
Поиск по сайту: