Постановка задачи оптимизации

Заданы множество и функция , определенная на множестве , требуется найти точки минимума или максимума.

Запишем задачу на минимум в виде:

где - целевая функция; - допустимое множество; - допустимая точка задачи.

Точка , являющаяся решением задачиможет быть точкой глобального или локального минимума.

Точка называется

1) точкой глобального минимума функции на множестве или глобальным решением задачи (1), если (2)

2) точка х* называется точкой локального минимума, если существует некоторая окрестность этой точки, в любой точки которой значение функции больше, чем в x* - f(x)>f(x*) (3).

Ясно, что глобальное решение является и локальным; обратное неверно.

Проиллюстрируем на рисунке понятия локального и глобального оптимума для функции одной переменной.

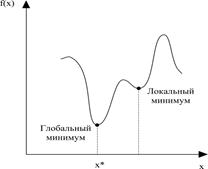
Для отражения того факта, что точка является точкой глобального минимума функции на множестве , обычно используется запись

или эквивалентная ей запись .

Множество всех точек глобального минимума на , обозначают через , где - минимальное значение функции на множестве . В этом случае - это просто произвольная точка из множества

Решения оптимизационных задач, то есть точки минимума и максимума функции на множестве , называются также точками экстремума, а сами задачи - экстремальными задачами.

Для применения теории оптимизации к решению конкретных задачи нужно выполнить определённую последовательность действий, которая называется постановкой задачи оптимизации. Она включает этапы:

1 установление границ подлежащей оптимизации системы;

2 выбор количественного критерия, позволяющего выявить наилучший вариант (характеристического критерия);

3 определение внутрисистемных переменных, через которые выражается характеристический критерий;

4 построение модели, которая описывает взаимосвязь внутрисистемных переменных.

2. Понятие и состав модели. Классификация задач оптимизации.

Методы оптимизации являются частью дисциплины исследование операций.

Исследование операций представляет собой комплекс научных методов для решения задач эффективного управления организационными системами.

Управление любой системой реализуется как процесс, подчиняющийся определенным закономерностям. Для этого все параметры, характеризующие процесс и внешние условия, должны быть количественно определены. Следовательно, цель исследования операций – количественное обоснование принимаемых решений по организации управления.

При решении конкретной задачи управления предполагается:

- построение экономических и математических моделей для принятия решений в сложных ситуациях или в условиях неопределенности;

- изучение взаимосвязей исследуемой системы и установление критериев эффективности, позволяющих оценивать преимущества того или иного варианта действия.

Критериев может быть много, тогда задача становится многокритериальной. Существуют методы решения многокритериальных задач, но можно привести многокритериальную задачу к однокритериальной. Для этого один из критериев выбирается в качестве первичного, а остальные становятся вторичными. Первичный критерий используется как характеристический, а вторичные формируют ограничения задачи.

Для применения методов оптимизации (количественных методов) требуется построить математическую модель. Модель представляет собой отражение реального объекта или процесса. В общем случае под термином «модель» понимается сложный объект, элементам которого можно поставить в соответствие элементы оригинала. При построении модели операция упрощается, схематизируется и схема операции описывается с помощью математического аппарата. Процесс построения модели называется моделированием.

Классификацию задач оптимизации можно проводить по нескольким признакам в зависимости от вида функции и множества :

1) детерминированные, стохастические, задачи оптимизации с неопределенностями;

а) Детерминированная модель отражает поведение системы с позиции полной определенности в настоящем и будущем. Примеры таких моделей: формулы физических законов, программы обработки деталей и т.д.

б) Вероятностная модель учитывает влияние случайных факторов на поведение системы и, следовательно, оценивает будущее с позиций вероятности тех или иных событий.

в) Игровая модель дает возможность изучать конфликтные ситуации, в которых каждая из конфликтных сторон придерживается своих взглядов, старается получить информацию о намерениях «противника» и действует в соответствии складывающейся обстановке.

2) статические, динамические (например, задачи управления). Математические модели могут отражать состояние, в котором находится исследуемая система в какой-то момент времени, или отражать изменения во времени, происходящие в экономической системе, т.е. описывать развитие системы во времени. Модели первого типа являются статическими, второго – динамическими. Если состояние системы описывается в каждый данный момент времени, то модели именуются непрерывными, если в некоторые фиксированные моменты времени, то – дискретными или моделями с дискретным временем.

3) безусловной и условной оптимизации. Если имеются ограничения на вектор , то задача (1) называется задачей оптимизации с ограничениями или задачей условной оптимизации.

4) однокритериальные и многокритериальные;

5) линейные и нелинейные. Задача условной оптимизации, в которой все функции линейны, называется задачей линейного программирования. Задачи с нелинейными целевой функцией или ограничениями называются задачами нелинейного программирования.

6) одномерные и многомерные, причем многомерные задачи могут быть малой и большой размерности. Если размерность вектора равна 1 ( =1), то задача (1) называется однопараметрической задачей оптимизации (одномерной задачей оптимизации). Если размерность вектора больше 1 ( >1), то задача (1) называется многопараметрической задачей оптимизации (многомерной задачей оптимизации).

7) одноэкстремальные и многоэкстремальные.

3. Линейное программирование. Виды задач линейного программирования: оптимального использования ресурсов и оптимизации годовой производственной программы предприятия.

Линейное программирование – это раздел матпрограммирования, применяемый при разработке методов нахождения экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные.

По типу решаемых задач методы ЛП разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП).

Главная особенность задач линейного программирования заключается в том, что экстремум целевой функции находится на границе области допустимых решений.

Рисунок 1 – Экстремум целевой функции

Математическая модель ЗЛП записывается следующим образом:

max (или min) Z=z(X), (1)

X Î D.

ОДР может быть представлена системой линейных уравнений или неравенств.

Вектор Х=(х₁, х₂,.... x _п) является вектором управления или управляющим воздействия.

Допустимый план Х, при котором критерий оптимальности Z=z(X) достигаетэкстремального значения, называется оптимальным и обозначается через X*, экстремальное значение целевой функции — через Z*=z(X*).

Поиск по сайту: