 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Правила построения двойственных задач
Выделяют следующие правила построения симметричных двойственных задач:
1) если прямая задача на максимум, то двойственная к ней – на минимум, и наоборот;
2) коэффициенты cj целевой функции прямой задачи являются свободными членами двойственной;
3) свободные члены bi ограничений прямой задачи являются коэффициентами целевой функции двойственной;
4) матрицы ограничений прямой и двойственной задач являются транспонированными друг другу;
5) если прямая задача на максимум, то ее система ограничений представляется в виде неравенств со знаком «≤». Двойственная задача решается на минимум, и ее система ограничений имеет вид неравенств со знаком «≥»;
6) число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной – числу переменных прямой;
7) все переменные в обеих задачах неотрицательны.
Если среди ограничений прямой задачи имеются равенства или на некоторые переменные не наложено условие неотрицательности, то, построив двойственную ей задачу, получим пару несимметричных двойственных задач.
Правила построения несимметричной двойственной задачи:
1) если на переменную xj прямой задачи наложено условие неотрицательности, то j-e условие системы ограничений двойственной задачи является неравенством;
2) если на переменную xj прямой задачи не наложено условие неотрицательности, то j-e условие системы ограничений двойственной задачи записывается в виде строгого равенства;
3) если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не накладывается условие неотрицательности.
11. Теоремы двойственности и их экономическое содержание.
Основное неравенство двойственности: Для любых допустимых решений X и Y пары двойственных задач ЛП справедливо неравенство:
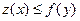 или
или  .
.
Экономически это означает, что для любого допустимого плана производства и любого допустимого вектора оценок ресурсов стоимость изготовленного продукта не превосходит оценки ресурсов.
Теорема существования (или малая теорема двойственности): Чтобы прямая и двойственная задачи имели оптимальное решение, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.
Первая основная теорема двойственности: если одна из пары двойственных задач имеет оптимальное решение, то и другая его имеет. Причем экстремальные значения их целевых функций равны. Если же целевая функция одной из задач не ограничена, то система ограничений другой противоречива.
Если цена реализации единицы продукции задается вышестоящими организациями, то yi называют внутренней оценкой ресурса. В этих терминах первая теорема двойственности интерпретируется следующим образом: допустимый план производства и вектор оценок ресурсов оказываются оптимальными тогда, когда объем реализации продукции, измеренный во внешних ценах, будет равен оценке всех ресурсов во внутренних ценах yi. В этом случае двойственные оценки выступают как инструмент балансирования затрат и результатов.
Требуется:
1) определить оптимальный план выпуска продукции, доставляющий предприятию максимум прибыли;
2) составить двойственную задачу.
Между переменными прямой и двойственной задачи можно установить следующее взаимно однозначное соответствие
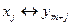 и
и  .
.
Получить решение двойственной задачи можно из последней симплексной таблицы прямой задачи. Если прямая задача решается на максимум, то оптимальное решение двойственной соответствует оценкам индексной строки в последней симплексной таблице прямой задачи, т.е. 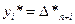 ,
, 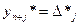 . Если прямая задача решается на минимум, то оптимальное решение двойственной соответствует оценкам индексной строки взятыми с противоположным знаком, т.е.
. Если прямая задача решается на минимум, то оптимальное решение двойственной соответствует оценкам индексной строки взятыми с противоположным знаком, т.е. 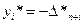 ,
, 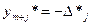 .
.
Вторая теорема двойственности (о дополняющей нежесткости): чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:
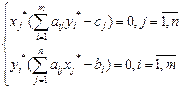 ,
,
т.е. если какое-либо ограничение одной задачи обращается ее оптимальным планом в строгое неравенство, то соответствующая переменная двойственной ей задачи в ее оптимальном плане равна нулю; если же какая-либо переменная оптимального решения одной задачи положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом обращается в точное равенство:
если  , то
, то 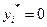 ;
;
если  , то
, то 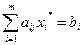 .
.
Аналогично,
если 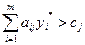 , то
, то  ;
;
если  , то
, то 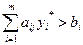 .
.
Отсюда следует, что оценки оптимального плана – это мера дефицитности ресурсов. Ресурсы 1-й, 2-й и 4-й являются дефицитными, 3-й ресурс – недефицитный.
Критерий оптимальности Канторовича: Чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно, чтобы значения целевых функций для них совпадали, т.е. z(x)=f(y).
Предположим, что величины ресурсов bi могут изменяться. Возникает вопрос, при каких приращениях правых частей ограничений найденный оптимальный план Х* не изменяется и как эти приращения сказываются на экстремальном значении целевой функции.
Третья теорема двойственности: Значения переменных yi в оптимальном решении равны изменению целевой функции при малом изменении соответствующего ограничения ресурса:
 .
.
Если принять 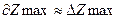 и
и 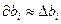 , то получим
, то получим 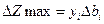 . Тогда при
. Тогда при 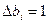 получим
получим 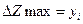 . Поэтому величина двойственной оценки численно равна изменению целевой функции при изменении соответствующего ресурса на единицу.
. Поэтому величина двойственной оценки численно равна изменению целевой функции при изменении соответствующего ресурса на единицу.
Чем выше величина оценки yi, тем острее дефицитность i-го ресурса.
Необходимо отметить, что ценность различных видов ресурсов нельзя отождествлять с действительными ценами, по которым осуществляется закупка. в данном случае речь идет о некоторой мере (мерке), имеющей экономическую природу, которая характеризует ценность ресурсов только относительно полученного оптимального решения.
Возникает вопрос – возможна ли замена одного ресурса другим.
Коэффициент взаимозаменяемости – показывает, сколько единиц ресурса i необходимо дополнительно приобрести, чтобы компенсировать уменьшение ресурса j на единицу:
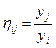 .
.
12. Математическая модель транспортной задачи: открытая и закрытая виды моделей.
Пусть имеется m (i=1;т) поставщиков, располагающих некоторым однородным продуктом в объемах по аi единиц, и n получателей с объемами потребления по bj единиц. Задана матрица C=| сij |, где сij — стоимость перевозки единицы продукции от i -го поставщика j -му потребителю. Возникает задача определения плана перевозок X=| xij |, где x ij — количество единиц продукции, поставляемой по коммуникации ij. Целевой функцией можно считать суммарную стоимость всех перевозок.
Условия задачи в табличном виде выглядят следующим образом:
| b1 | b2 | ... | bj | ... | bn | |
| a1 | x11 c11 | x12 c12 | ... | x1j c1j | ... | x1n c1n |
| a2 | x21 c21 | x22 c22 | ... | x2j c2j | ... | x2n c2n |
| ... | ... | ... | ... | ... | ... | ... |
| ai | xi1 ci1 | xi2 ci2 | ... | xij cij | ... | xin cin |
| ... | ... | ... | ... | ... | ... | ... |
| am | xm1 cm1 | xm2 cm2 | ... | xmj cmj | ... | xmn cmn |
Если 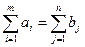 (1)
(1)
то задача называется закрытой, в противном случае — открытой.
Математическую модель закрытой задачи выглядит следующим образом.
Функция цели — минимизация суммарных затрат на перевозку продукции
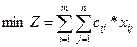 . (2)
. (2)
при ограничениях:
1) на запасы продукции у поставщиков
 (3)
(3)
2) на запросы потребителей, которые должны быть полностью удовлетворены,
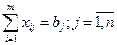 (4)
(4)
3) условия неотрицательности, исключающие обратные перевозки:
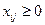 . (5)
. (5)
Матрицу X=| xij |, удовлетворяющую ограничениям, называют допустимым планом перевозок, а переменные xij — допустимыми перевозками.
Графический способ задания условий задачи

Допустимый план Х, доставляющий целевой функции минимальное значение именуется оптимальным; С=|| сij || называется матрицей тарифов или матрицей транспортных издержек. Отрезок или линия, соединяющая i-го поставщика с j-м потребителем, называется коммуникацией и обозначается (ij) или (AiBj). Если на всех коммуникациях (ij) проставлены величины перевозок хij, то получается транспортная сеть.
Если условие  не выполняется, то модель транспортной задачи называется открытой. В случае, если запасы поставщиков больше потребностей получателей, вводят n+1 –гo фиктивного потребителя, запросы которого равны излишкам запаса, т. е.
не выполняется, то модель транспортной задачи называется открытой. В случае, если запасы поставщиков больше потребностей получателей, вводят n+1 –гo фиктивного потребителя, запросы которого равны излишкам запаса, т. е.
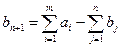 .
.
Тарифы Ci;n+1 считают равными нулю. Получим расширенную закрытую задачу. Ее оптимальный план даст оптимальный план исходной задачи. Поставки х i;n+1 в оптимальном плане расширенной задачи покажут остатки продукции на складах поставщиков.
Если потребности превышают запасы, то вводят m+1 -ro фиктивного поставщика. Его запасы считают равными недостающей продукции:
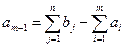 .
.
Тарифы сm+1;j равны некоторому большому положительному числу М. В расширенной задаче получим баланс потребностей и запасов. Поставки xm+1;j в оптимальном плане расширенной задачи покажут объемы недостачи продукции.
Чтобы запасы от поставщиков были вывезены и потребности получателей были удовлетворены полностью, необходимо и достаточно выполнить условие равенства  .
.
13. Построение начального опорного плана транспортной задачи: метод северо-западного угла и минимального элемента.
Модель транспортной задачи — задача линейного программирования. Ее оптимальный план всегда можно найти симплексным методом. Однако матрица системы ограничений специфична.
Специфика заключается в следующем:
1) Коэффициенты при неизвестных во всех ограничениях равны единице.
2) Каждая неизвестная величина встречается в двух и только в двух уравнениях: один раз — в системе (3) и один раз — в системе (4).
3) Система уравнений симметрична относительно всех переменных хij.
Благодаря этой специфике общую процедуру симплексного метода применительно к транспортной задаче можно значительно упростить. При любом методе ее решение начинают с нахождения начального опорного плана. В невырожденном опорном плане ЗЛП должно содержаться f отличных от нуля координат, где f — ранг системы ограничений. В системе ограничений уравнений закрытой транспортной задачи имеется m+n—1 линейно независимых уравнений, т. е. ранг системы ограничений (3—4) равен m + n—1.
Способ северо-западного угла предполагает начать работу с клетки (1, 1) (на географической карте это соответствует северо-западному углу, отсюда — название способа). Предположим, что x11=min{a1, b1}.
а) Если a1 > b1, то х11 = b1, т.е запросы первого потребителя будут полностью удовлетворены. В дальнейшем первый столбец в расчет не принимается, в нем переменные хi1=0; i=2,m. Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1;2) меньшее из чисел (a1 - b1) и a1 > b2, т.е x11=min{a1- b1; b2}. когда запасы первого поставщика исчерпаны, то дальнейшие расчеты производятся по второй строке и т.д.
б) Если a1 < b1, то x11=a1, при этом запас первого поставщика будет полностью исчерпан, поэтому x1j=0, j=2;n. Первая строка из дальнейшего рассмотрения исключается.
Аналогично производятся вычисления во всех остальных строках. План перевозок, построенный по такому способу, содержит m+n—1 заполненных клеток, т. е. является опорным.
Недостаток способа: он не учитывает матрицы тарифов. Поэтому опорный план может оказаться далеким от оптимального.
Способ минимального элемента. В данном методе рассматриваются тарифы и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать n+m-1 заполненных клеток.
В процессе заполнения таблицы могут быть одновременно исключены и столбец и строка. Такое возможно в случае, когда исчерпан запас поставщика и полностью удовлетворен спрос потребителя. Полученный план будет вырожденным, т.к. не выполняется условие равенства количества занятых клеток величине n+m-1. В этом случае в свободную клетку необходимо записать число «0» – «ноль-загрузка», условно считая эту клетку занятой. Однако число «0» записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Циклом в матрице называется непрерывная замкнутая ломанная линия, вершины которой находятся в клетках матрицы, а звенья расположены вдоль строк и столбцов. При чем в каждой вершине цикла встречается ровно два звена, одно из нихрасположено по строке, второе – по столбцу. Если цикл образует самопересекающаяся ломанная линия, то точки ее самопересечения вершин необразуются.
Циклы в матрице тарифов удовлетворяю следующим свойствам:
1) число вершин в каждом цикле четно;
2) одна вершин цикла должна быть свободной клеткой, все остальные – занятыми.
14. Построение начального опорного плана транспортной задачи: метод Фогеля и минимального элемента.
Модель транспортной задачи — задача линейного программирования. Ее оптимальный план всегда можно найти симплексным методом. Однако матрица системы ограничений специфична.
Специфика заключается в следующем:
1) Коэффициенты при неизвестных во всех ограничениях равны единице.
2) Каждая неизвестная величина встречается в двух и только в двух уравнениях: один раз — в системе (3) и один раз — в системе (4).
3) Система уравнений симметрична относительно всех переменных хij.
Благодаря этой специфике общую процедуру симплексного метода применительно к транспортной задаче можно значительно упростить. При любом методе ее решение начинают с нахождения начального опорного плана. В невырожденном опорном плане ЗЛП должно содержаться f отличных от нуля координат, где f — ранг системы ограничений. В системе ограничений уравнений закрытой транспортной задачи имеется m+n—1 линейно независимых уравнений, т. е. ранг системы ограничений (3—4) равен m + n—1.
Метод Фогеля. В распределительной таблице по строкам и столбцам определяют разность между двумя наименьшими тарифами. Максимальную разность отмечают знаком «». Далее в строке (или в столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (или столбцы) с нулевыми остатками груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится по рассмотренным ранее правилам.
Способ минимального элемента. В данном методе рассматриваются тарифы и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать n+m-1 заполненных клеток.
В процессе заполнения таблицы могут быть одновременно исключены и столбец и строка. Такое возможно в случае, когда исчерпан запас поставщика и полностью удовлетворен спрос потребителя. Полученный план будет вырожденным, т.к. не выполняется условие равенства количества занятых клеток величине n+m-1. В этом случае в свободную клетку необходимо записать число «0» – «ноль-загрузка», условно считая эту клетку занятой. Однако число «0» записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Циклом в матрице называется непрерывная замкнутая ломанная линия, вершины которой находятся в клетках матрицы, а звенья расположены вдоль строк и столбцов. При чем в каждой вершине цикла встречается ровно два звена, одно из них расположено по строке, второе – по столбцу. Если цикл образует самопересекающаяся ломанная линия, то точки ее самопересечения вершин не образуются. Примеры циклов:

Циклы в матрице тарифов удовлетворяю следующим свойствам:
3) число вершин в каждом цикле четно;
4) одна вершин цикла должна быть свободной клеткой, все остальные – занятыми.
15. Транспортная задача: условия оптимальности опорного плана, метод потенциалов.
Потенциалы иi и vj приписываются каждому поставщику и потребителю. Всего потенциалов п+m. Для заполненных клеток, которых т+п— 1, выполняются условие
 .
.
Они служат теми уравнениями, из которых находят значения потенциалов. Эта система уравнений имеет бесчисленное множество решений, любое из которых составит искомую систему потенциалов. Чтобы найти какое-либо одно решение, значение одного из потенциалов нужно выбрать произвольно. Остальные устанавливаются из системы уравнений для заполненных клеток. Обычно считают, что u1 = 0, и вычисляют остальные потенциалы.
Для каждой клетки вычисляют оценки:
 .
.
Если опорный допустимый план оптимален, то  ≥ 0. Если же есть хоть одна отрицательная оценка, то план не оптимален. Тогда в базис вводят клетку с минимальной оценкой. Эту клетку называют перспективной.
≥ 0. Если же есть хоть одна отрицательная оценка, то план не оптимален. Тогда в базис вводят клетку с минимальной оценкой. Эту клетку называют перспективной.
Экономический смысл оценки  в том, что она показывает, на сколько можно уменьшить транспортные издержки при загрузке данной клетки единицей груза.
в том, что она показывает, на сколько можно уменьшить транспортные издержки при загрузке данной клетки единицей груза.
Для улучшения опорного плана для перспективной свободной клетки строится замкнутый цикл. Вершинам этого цикла присваиваются знаки: свободной клетке – «плюс», следующей по часовой или против часовой стрелки клетке – знак «минус», следующей клетки – «плюс» и т.д.
В клетках с отрицательными вершинами выбирается минимальное количество груза λ, которое будет перемещаться по циклу. Оно прибавляется к грузу в вершинах с положительным знакам и вычитаться из поставок в отрицательных вершинах. В результате подобных вычислений баланс не нарушается.
Алгоритм метода потенциалов:
1) построить опорный план по одному из правил;
2) вычислить потенциалы поставщиков и потребителей 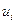 и
и 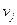 , решив систему уравнений
, решив систему уравнений  ;
;
3) вычислить оценки 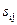 для всех свободных клеток. Если все
для всех свободных клеток. Если все 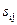 ≥ 0, то опорный план оптимален. Если же для всех свободных клеток
≥ 0, то опорный план оптимален. Если же для всех свободных клеток 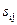 > 0, то оптимальный план единственный. Если же хоть для одной свободной оценки
> 0, то оптимальный план единственный. Если же хоть для одной свободной оценки 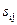 =0, то имеется бесчисленное множество оптимальных планов с одним и тем же значением целевой функции;
=0, то имеется бесчисленное множество оптимальных планов с одним и тем же значением целевой функции;
4) в случае если есть 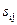 < 0, то строиться цикл, расчетная таблица заполняется заново и алгоритм начинается с пункта 2.
< 0, то строиться цикл, расчетная таблица заполняется заново и алгоритм начинается с пункта 2.
Поиск по сайту: