АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Первая интерполяционная формула Ньютона

Читайте также:
  1. I этап—первая неделя.
  2. I. 4.1. Первая теорема двойственности
  3. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  4. II Формула Тейлора с остаточным членом в форме Пеано
  5. II. Первая помощь в различных случаях
  6. III Формула Тейлора с остаточным членом в форме Лагранжа
  7. А) Первая благородная истина
  8. А) Первая предпосылка: анализ как ситуация кризиса.
  9. Асть первая - теоретическая
  10. Барометрическая формула
  11. Барометрическая формула. Распределение Больцмана.
  12. Барометрическая формула. Распределение Больцмана.

Пусть в равноотстоящих точках , где h – шаг интерполяции, заданы значения для функции . Требуется подобрать полином степени не выше n, удовлетворяющий условиям (1).
Введем конечные разности для последовательности значений :

(2)

Условия (1) эквивалентны равенствам:

при

Опуская выкладки, приведенные в [1], окончательно получим первую интерполяционную формулу Ньютона:

(3)

где – число шагов интерполяции от начальной точки до точки х.
Формулу (3) целесообразно использовать для интерполяции функции в окрестности начальной точки , где q по абсолютной величине мало.

В частных случаях имеем:

при n = 1 – формулу линейной интерполяции:

;

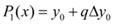при n = 2 – формулу квадратичной или параболической интерполяции:


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)