Интерполирование сплайнами

Интерполяционные формулы Лагранжа, Ньютона и Стирлинга и др. при использовании большого числа узлов интерполяции на всем отрезке [ a, b ] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений [2]. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей весь отрезок [ a, b ] разбивается на частичные отрезки и на каждом из них функцию 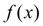заменяют приближенно полиномом невысокой степени. Это называется кусочно-полиномиальной интерполяцией.

Один из способов интерполирования на всем отрезке [ a, b ] является интерполирование сплайнами.

Сплайном называется кусочно-полиномиальная функция, определенная на отрезке [ a, b ] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.

Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции кубическим сплайном.

Пусть на отрезке [ a, b ] задана непрерывная функция 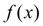. Введем разбиение отрезка:

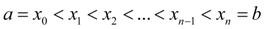(6)

и обозначим , .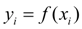

Сплайном, соответствующим данной функции 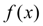и узлам интерполяции (6) называется функция 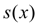, удовлетворяющая следующим условиям:

1) на каждом отрезке 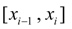, 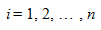функция 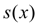является кубическим многочленом;

2) функция 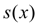, а также ее первая и вторая производные непрерывны на отрезке [ a, b ];

3)

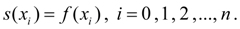
Третье условие называется условием интерполирования. Сплайн, определяемый условиями 1) – 3), называется интерполяционным кубическим сплайном.

Рассмотрим способ построения кубического сплайна [2].

На каждом из отрезков 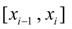, 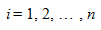будем искать сплайн-функцию 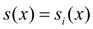в виде полинома третьей степени:

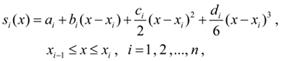(7)

где искомые коэффициенты.

Продифференцируем (7) трижды по х:

откуда следует

Из условия интерполирования 3) получаем:

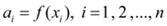. (8)

Кроме того, будем считать .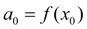

Из условий непрерывности функции 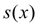вытекает:

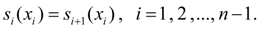
Отсюда с учетом (7) получим:

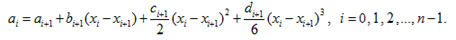
Обозначив 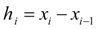и опуская промежуточные выкладки [2], окончательно получим систему уравнений для определения коэффициентов :

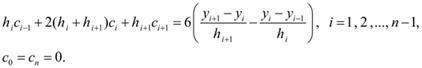(9)

В силу трехдиагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты , остальные коэффициенты определим по явным формулам:

(10)

Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) – 3).

Заключение

В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций, оказывается, эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.

Список литературы

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.

2. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 430 с.

3. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. Изд-во "Лаборатория базовых знаний". 2003.

Поиск по сайту: