Склад вимірювальної установки та теорія вимірювань

Вимірювання коефіцієнта відбиття – важлива практична задача. Коефіцієнт відбиття дозволяє зробити висновок про ступінь узгодження, тобто ефективність передавання НВЧ енергії в навантаження, наявність стоячої хвилі, яка впливає на рівень сигналів, що можуть бути переданими по лінії НВЧ. Перетворення частотної залежності коефіцієнта відбиття за допомогою трансформації Фур’є в часову (просторову) область дозволяє локалізувати неоднорідності в НВЧ тракті, пристроях. На рис. 4.1 показана мостова схема вимірювання коефіцієнта відбиття з використанням подвійного хвилевідного трійника.

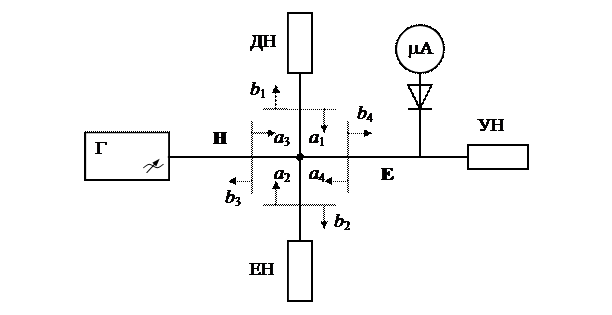
Рис.4.1. Мостова схема вимірювання коефіцієнта відбиття

До Н -плеча подвійного хвилевідного трійника підключається генератор НВЧ коливань, до одного з бічних плечей – еталонне навантаження, до іншого – досліджуване навантаження, до Е -плеча – детекторна секція. Коефіцієнти відбиття від двох порівнюваних навантажень – еталонного (плече 2) і досліджуваного (плече 1) – можна виразити в такий спосіб:

, , (4.1)

де а ₁, а ₂, b ₁, b ₂ – відповідно амплітуди електричного поля падаючих (вхідних) і відбитих (вихідних) хвиль для кожного з бічних плечей. Якщо міст збалансований, тобто відбита хвиля в Е -плечі відсутня (b ₄ = 0), то Г ₁ = Г ₂.

Розглянемо матричний вираз

, (4.2)

де – матриця розсіювання подвійного хвилевідного трійника, – матриця впливів, – матриця відгуків розглянутого пристрою. При а ₄ = 0 випливає, що

. (4.3)

Для випадку b ₄ = 0 завжди виконується а ₄ = 0, незалежно від того, узгоджений детектор чи ні. Якщо міст збалансований (b ₄ = 0, s ₁₄¹0), то з виразу (4.3) випливає, що а ₁ = а ₂. За тих самих умов справедливо

, , (4.4)

З того, що а ₁ = а ₂, випливає b ₁ = b ₂. Отже, якщо міст збалансований, то співвідношення (4.1) правильні.

Замінивши в плечі 2 еталонне навантаження на погоджене , можна вимірювати модуль коефіцієнта відбиття |Г₁| у плечі 1. Завдяки узгодженню в плечах 2 і 4 (а ₂ = а ₄ = 0) і з огляду на те, що Г₁ = а ₁ /b ₁ з рівняння (4.2) одержуємо

. (4.5)

Згідно з цими ж рівняннями

звідки випливає

(4.6)

З виразів (4.5), (4.6) маємо

(4.7)

Тепер, щоб обчислити коефіцієнт відбиття Г₁, потрібно підставити значення елементів матриці розсіювання s_ij для подвійного Т-моста, а також визначити відношення b ₄ /a ₃. Пряме вимірювання цієї величини провести важко. Простіше вимірити потужність P _д у плечі 4, якщо при цьому потужність P _г, щовіддається генератором, залишається постійною, що може бути реалізовано практично. Із співвідношення (4.7) можна одержати такий вираз:

. (4.8)

Для випадку невеликої внутрішньої неузгодженості моста ½ s ₁₁½<< 1 маємо

. (4.9)

У випадку використання цілком погодженого моста, у якого , , маємо

. (4.10)

Отримане співвідношення дозволяє розрахувати ½Г₁½ із задовільною точністю.

Поиск по сайту: