 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
К графику функции
| Определение касательной к графику функции | Касательной к графику функции в точке  называют предельное положение секущей, соединяющей точки называют предельное положение секущей, соединяющей точки  и и  графика, при стремлении точки графика, при стремлении точки 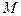 к точке к точке  по графику. по графику.
|
| Геометрический смысл производной | Производная функции  в точке в точке  равна тангенсу угла, образованного касательной к графику функции в этой точке и положительным направлением оси равна тангенсу угла, образованного касательной к графику функции в этой точке и положительным направлением оси  : :
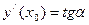 ,
где ,
где  - угол между касательной к графику функции в точке - угол между касательной к графику функции в точке  и положительным направлением оси и положительным направлением оси  . .
|
| Уравнение касательной | Пусть функция  в точке в точке  имеет производную имеет производную  . Тогда в точке . Тогда в точке  существует касательная к графику этой функции, уравнение которой: существует касательная к графику этой функции, уравнение которой:
 . .
|
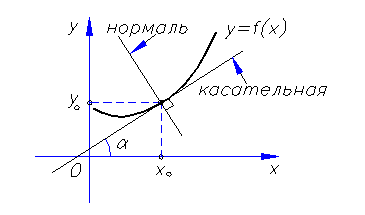
| Определение нормали | Прямая линия, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой. |
| Уравнение нормали | Пусть функция  в точке в точке  имеет производную имеет производную  . Тогда в точке . Тогда в точке  существует нормаль к графику этой функции, уравнение которой: существует нормаль к графику этой функции, уравнение которой:
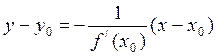 .
Если .
Если  (то есть касательная горизонтальна), то нормаль вертикальна и имеет уравнение (то есть касательная горизонтальна), то нормаль вертикальна и имеет уравнение 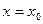 . .
|
Поиск по сайту: