Высших порядков

Определение производной второго порядка

Производная от функции (производной первого порядка) называется производной второго порядка от функции (или второй производной) и обозначается .

Определение производной n – го порядка

Производная от функции (производной эн-минус первого порядка) называется производной энного порядка от функции (или энной производной) и обозначается .

,

поскольку при каждом последовательном дифференцировании добавляется множитель .

Производная высших порядков параметрически заданной функции

Производная второго порядка функции, заданной параметрически уравнениями , может быть найдена по формуле: , а производная энного порядка – по формуле: .

Найдем сначала производную первого порядка функции .

.

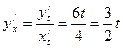Производная второго порядка данной функции равна .

ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И КОШИ

Теорема Ферма.
Если функция у = f (х), определенная в интервале (а; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.

Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).

Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [ а; b ] и дифференцируемая в интервале (а; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а; b) существует такая точка с, что f ′(с) = 0.
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).

Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [ а; b ] и дифференцируема в интервале (а; b), то в этом интервале найдется такая точка с, что

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ.

Следствие. Если f ′(x) = 0 в интервале (а; b), то в этом интервале функция f (х) постоянна.

Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [ а; b ];

2) дифференцируемы в интервале (а; b);

3) g' (x) ≠ 0 в этом интервале,

то в интервале (а; b) существует такая точка с, что имеет место равенство

Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа или .

Пусть a является некоторым конечным действительным числом или равно бесконечности.

· Если и , то ;

· Если и , то аналогично .

• Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенности можно свести к типу или с помощью алгебраических преобразований. А неопределенности сводятся к типу с помощью соотношения
• 
• Правило Лопиталя справедливо также и для односторонних пределов.

· Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

· Формула Тейлора

·, где R_n(x) - остаточный член формулы Тейлора.

· Остаточный член формулы Тейлора

· В форме Лагранжа:

· В форме Коши:

· Если после изучения данного теоретического материала (Формула Тейлора) у Вас возникли проблемы при решении задач на данную тему или появились вопросы образовательного характера, то Вы всегда можете задать их на нашем

ТАБЛИЦА ПРОИЗВОДНЫХ

1.

Поиск по сайту: