 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифференцирования функций
| Основные правила дифференцирова-ния функций | Пусть с – константа, а  и и  имеют производные в некоторой точке x. Тогда функции имеют производные в некоторой точке x. Тогда функции 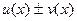 , ,  , ,  и и  (где (где  ) также имеют производные в этой точке, причем
1. ) также имеют производные в этой точке, причем
1.  - производная суммы функций равна сумме производных этих функций;
2. - производная суммы функций равна сумме производных этих функций;
2.  - производная произведенияфункций равна сумме произведений производной первой функции на вторую и первой функции на производную второй;
3. - производная произведенияфункций равна сумме произведений производной первой функции на вторую и первой функции на производную второй;
3.  , ,  - постоянный множитель выносят за знак производной;
4. - постоянный множитель выносят за знак производной;
4.  - производная отношения двух функций (частного) равна отношению разности произведений производной числителя на знаменатель и числителя на производную знаменателя к квадрату знаменателя;
5. пусть функция - производная отношения двух функций (частного) равна отношению разности произведений производной числителя на знаменатель и числителя на производную знаменателя к квадрату знаменателя;
5. пусть функция  имеет производную в точке имеет производную в точке  , а функция , а функция  - в точке - в точке  . Тогда сложнаяфункция . Тогда сложнаяфункция  также имеет производную в точке также имеет производную в точке  , причем , причем
 - производная сложной функции равна производной этой функции по промежуточному аргументу u, умноженной на производную от промежуточного аргумента u по основному аргументу x. - производная сложной функции равна производной этой функции по промежуточному аргументу u, умноженной на производную от промежуточного аргумента u по основному аргументу x.
|
Поиск по сайту: