 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифференциал функции в точке
| Определение дифференцируемой в точке функции | Пусть функция  определена в некоторой окрестности точки определена в некоторой окрестности точки  . Если приращение . Если приращение 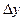 функции функции  можно представить в виде можно представить в виде
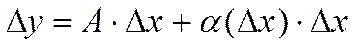 ,
где A – постоянное число в точке ,
где A – постоянное число в точке 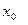 ; ;
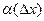 - бесконечно малая функция при - бесконечно малая функция при  ,
то функция ,
то функция  называется дифференцируемой в точке называется дифференцируемой в точке 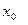 . .
|
| Определение дифференциала функции | Главная часть приращения 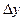 дифференцируемой в точке дифференцируемой в точке 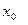 функции функции  , то есть , то есть
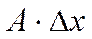 называется дифференциалом функции в точке
называется дифференциалом функции в точке 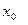 и обозначается
и обозначается 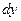 или или 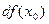 : :
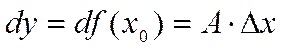 .
Замечание. Если .
Замечание. Если 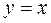 , то , то 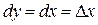 . .
|
| Теорема о связи функции, имеющей производную, и дифференцируемой в точке | Функция  дифференцируема в точке дифференцируема в точке 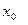 тогда и только тогда, когда в этой точке существует конечная производная тогда и только тогда, когда в этой точке существует конечная производная 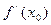 , при этом , при этом 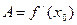 . Следовательно, . Следовательно, 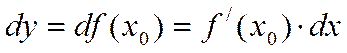 . .
|
| Геометрический смысл дифференциала | Дифференциал функции в точке  равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента 
|
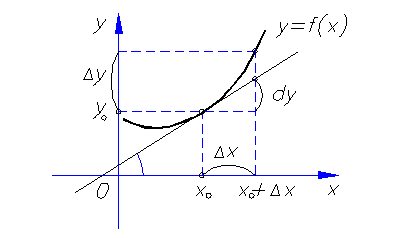
| Теорема о непрерывности дифференцируемой функции | Если функция дифференцируема в точке  , то она и непрерывна в этой точке. , то она и непрерывна в этой точке.
|
Поиск по сайту: