КОНТРОЛЬНАЯ РАБОТА №1

1. Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону х = 10 + 5 t – 10 t ² ? Масса тела 2 кг.

2. Найти закон движения тела массой 1 кг под действием постоянной силы 10 Н, если в момент t = 0 тело покоилось в начале координат (х = 0).

3. Найти закон движения тела массой 1 кг под действием постоянной силы 1 Н, если в момент t = 0 начальная координата х = 0 и ν₀ = 5 м/с.

4. Найти закон движения тела массой 1 кг под действием постоянной силы 2 Н, если в момент t = 0 имеем х₀ = 1 и ν₀ = 2 м/с.

5. Тело массой 2 кг движется с ускорением, изменяющимся по закону

а = 5 t – 10. Определить силу, действующую на тело через 5с после начала действия, и скорость в конце пятой секунды.

6. Сплошной шар массой 1 кг и радиусом 5 см вращается оси, проходящей через его центр. Закон вращения шара выражается уравнением

φ =10 + 5 t - 2 t ². В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.

7. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением

s = 100 + 10 t - 0,5 t ². Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.

8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением

s = t ³ + 4 t ² - t +8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала ее движения.

9. Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8 t - 0,2 t ³. Найти скорость, тангенциальное‚ нормальное и полное ускорение в момент времени З с.

10. Тело вращается равноускоренно с начальной угловой скоростью 5 с^-1 и угловым ускорением 1 с^-2. Сколько оборотов сделает тело за 10 с?

11. Параллелепипед размером 2 × 2 × 4 см³ движется параллельно большему ребру. При какой скорости движения он будет казаться кубом.

12. Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?

13. π -мезон – нестабильная частица. Собственное время жизни его

2,6 ∙ 10^-8 с. Какое расстояние пролетит π -мезон до распада, если он движется со скоростью 0,9 с?

14. Найти собственное время жизни нестабильной частицы μ -мезона, движущегося со скоростью 0,99 с, если расстояние, пролетаемое им до распада, равно 0,1 км.

15. Собственное время жизни π -мезона 2,6 ∙ 10^-8 с. Чему равно время жизни π -мезона для наблюдателя, относительно которого эта частица движется со скоростью 0,8 с?

16. Электрон, скорость которого 0,9 с, движется навстречу протону, имеющему скорость 0,8 с. Определять скорость их относительного движения.

17. Радиоактивное ядро, вылетевшее из ускорителя со скоростью 0,8 с, выбросило в направлении своего движения β -частицу со скоростью 0,7 с относительно ускорителя. Найти скорость частицы относительно ядра.

18. Две частицы движутся навстречу друг другу со скоростью 0,8 с. Определить скорость их относительного движения.

19. При какой скорости движения релятивистское сокращение длины движущегося тела составит 25%.

20. Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились на 75%.

21. Сплошной цилиндр массой 0,1 кг катится без скольжения с постоянной скоростью 4 м/с. Определить кинетическую энергию цилиндра, время до его остановки, если на него действует сила трения 0,1 Н.

22. Сплошной шар скатывается по наклонной плоскости, длина которой 1 м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.

23. Полый цилиндр массой 1 кг катится по горизонтальной поверхности со скоростью 10 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 2м.

24. Маховик, имеющий форму диска массой 10 кг и радиусом 0,1 м, был

раскручен до частоты 120 мин^-1. Под действием силы трения диск остановился

через 10 с. Найти момент сил трения, считая его постоянным.

25. Обруч и диск скатываются с наклонной плоскости, составляющей угол 30° с горизонтом. Чему равны их ускорения в конце спуска? Силой трения пренебречь.

26. С покоящимся шаром массой 2 кг сталкивается такой же шар, движущийся со скоростью 1 м/с. Вычислить работу, совершенную вследствие деформации при прямом центральном неупругом ударе.

27. Масса снаряда 10 кг, масса ствола орудия 500 кг. При выстреле снаряд получает кинетическую энергию 1,5 ∙ 10⁶ Дж. Какую кинетическую энергию получает ствол орудия вследствие отдачи?

28. Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 2 кг со скоростью 10 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед 0,02.

29. Молекула водорода, двигающаяся со скоростью 400 м/с, подлетает к стенке сосуда под углом 60° и упруго ударяется о нее. Определить импульс, полученный стенкой. Принять массу молекул равной 3 ∙ 10^-27 кг.

30. Стальной шарик массой 50 г упал с высоты 1 м на большую плиту, передав ей импульс силы, равный 0,27 Н ∙ с. Определить количество теплоты выделившегося при ударе и высоту, на которую поднимается шарик.

31. С какой скоростью движется электрон, если его кинетическая энергия 1,02 МэВ? Определять импульс электрона.

32. Кинетическая энергия частицы оказалась равной ее энергии покоя. Какова скорость этой частицы?

33. Масса движущегося протона 2,5 ∙ 10^-27 кг. Найти скорость и кинетическую энергию протона.

34. Протон прошел ускоряющую разность потенциалов в 200 МВ. Во сколько раз его релятивистская масса больше массы покоя? Чему равна скорость протона?

35. Определить скорость электрона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергию электрона.

36. Вычислить скорость, полную и кинетическую энергию протона в тот момент, когда его масса равна массе покоя α -частицы.

37. Найти импульс, полную и кинетическую энергию электрона, движущегося со скоростью, равной 0,7 с.

38. Протон и α -частица проходят одинаковую ускоряющую разность потенциалов, после чего масса протона составила половину массы покоя

α -частицы. Определить разность потенциалов.

39. Найти импульс, полную и кинетическую энергию нейтрона, движущегося со скоростью 0,6 с.

40. Во сколько раз масса движущегося дейтрона больше массы движущегося электрона, если их скорости соответственно равны 0,6 с и 0,9 с. Чему равны их кинетические энергии.

41. Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0,20 г водорода при температуре 27 °С.

42. Давление идеального газа 10 мПа, концентрация молекул

2 ∙ 10¹² см^-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.

43. Определить среднее значение полной кинетической энергии одной молекулы аргона и водяного пара при температуре 500К.

44. Средняя кинетическая энергия поступательного движения молекул газа равна 15 ∙ 10^-21 Дж. Концентрация молекул равна 9 ∙ 10¹⁹ см^-3. Определить давление газа.

45. В баллоне емкостью 50 л находится сжатый водород при 27 °С. После того как часть воздуха выпустили, давление понизилось на 1 ∙ 10⁵ Па. Определить массу выпущенного водорода. Процесс считать изотермическим.

46. В сосуде, имеющем форму шара, радиус которого 0,1 м, находится 5,6 г азота. До какой температуры можно нагреть сосуд если его стенки выдерживают давление 5 ∙ 10⁵ Па?

47. При температуре 300 К и давления 1,2 ∙ 10⁵ Па плотность смеси водорода и азота 1 кг/м³. Определить молярную массу смеси.

48. В баллоне емкостью 0,8 м³ находится 2 кг водорода и 2,9 кг азота. Определять давление смеси, если температура окружающей среды 27 °С.

49. До какой температуры можно нагреть запаянный сосуд, содержащий 36 г воды, чтобы он не разорвался, если известно, что стенки сосуда выдерживают давление 5 ∙ 10⁶ Па. Объем сосуда 5 л.

50. При температуре 27 °С и давлении 10⁶ Па плотность смеси кислорода и азота 12 г/дм³. Определить молярную массу смеси.

51. В сосуде емкостью 1 л содержится кислород массой 32 г. Определить среднее число соударений молекул в секунду при температуре 100 К.

52. Определить среднюю длину и среднюю продолжительность свободного пробега молекул углекислого газа при температуре 400 К и давлении 1,38 Па.

53. В сосуде емкостью 1 л находятся 4,4 г углекислого газа. Определить среднюю длину свободного пробега молекул.

54. Определить коэффициент диффузии гелия при давлении 1 ∙ 10⁶ Па и температуре 27 °С.

55. Определить коэффициент внутреннего трения кислорода при температуре 400 К.

56. В сосуде емкостью 5 л содержится 40 г аргона. Определить среднее число соударений молекул в секунду при температуре 400 К.

57. Определить коэффициент внутреннего трения воздуха при температуре 100 К.

58. Определить коэффициент диффузии азота при давлении 0,5 ∙ 10⁵ Па и температуре 127 °С.

59. Коэффициент внутреннего трения кислорода при нормальных условиях 1,9 ∙ 10^-4 кг/м ∙ с. Определить коэффициент теплопроводности кислорода.

60. Коэффициент диффузии водорода при нормальных условиях

9,1 ∙ 10^-5 м²/с. Определить коэффициент теплопроводности водорода.

61. Определить, какое количество теплоты необходимо сообщить аргону массой 400 г, чтобы нагреть его на 100 К: а) при постоянном объеме; б) при постоянном давлении.

62. Во сколько раз увеличится объем 2 молей кислорода при изотермическом расширений при температуре 300 К, если при этом газу сообщили 4 кДж теплоты.

63. Какое количество теплоты нужно сообщать 2 молям воздуха, чтобы он совершил работу в 1000 Дж: а) при изотермическом процессе; б) при изобарическом процессе.

64. Найти работу и изменение внутренней энергии при адиабатном расширении 28 г азота, если его объем увеличился в два раза. Начальная температура азота 27 °С.

65. Кислород, занимающий объем 10 л и находящийся под давлением

2 ∙ 10⁵ Па, адиабатно сжат до объема 2 л. Найти работу сжатия и изменение внутренней энергии кислорода.

66. Определить количество теплоты, сообщенное 88 г углекислого газа, если он был изобарически нагрет от 300 К до 350 К. Какую работу при этом может совершить газ и как изменится его внутренняя энергия?

67. При каком процессе выгоднее производить расширение воздуха: изобарическом или изотермическом, если объем увеличивается в пять раз. Начальная температура газа в обоих случаях одинаковая.

68. При каком процессе выгоднее производить нагревание 2 молей аргона на 100 К: а) изобарическом; б) изохорическом.

69. Азоту массой 20 г при изобарическом нагревании сообщили 3116 Дж теплоты. Как изменялась температура и внутренняя энергия газа.

70. При изотермическом расширении одного моля водорода была затрачена теплота 4 кДж, при этом объем водорода увеличился в пять раз. При какой температуре протекает процесс? Чему равно изменение внутренней энергии газа, какую работу совершает газ?

71. Определить изменение энтропии 14 г азота при изобарном нагревании его от 27 °С до 127 °С.

72. Как изменится энтропия 2 молей углекислого газа при изотермическом расширении, если объем газа увеличивается в четыре раза.

73. Совершая цикл Карно, газ отдал холодильнику 0,65 теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 400 К.

74. Тепловая машина работает по циклу Карно, к.п.д. которого 0,4. Каков будет к.п.д. этой машины, если она будет совершать тот же цикл в обратном направлении?

75. Холодильная машина работает по обратному циклу Карно, к.п.д. которого 400%. Каков будет к.п.д. этой машины, если она работает по прямому циклу Карно.

76. При прямом цикле Карно тепловая машина совершает работу

1000 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя.

77. Найти изменение энтропии при нагревании 2 кг воды от 0 до 100 °С и последующем превращении ее в пар при той же температуре.

78. Найти изменение энтропии при плавлении 2 кг свинца и дальнейшем его охлаждении от 327 до 0 °С.

79. Определить изменение энтропии, происходящее при смешивании 2 кг воды, находящихся при температуре 300 К, и 4 кг воды при температуре 370 К.

80. Лед массой 1 кг, находящийся при температуре 0°С, нагревают до температуры 57 °С. Определить изменение энтропии.

http://reshuzadachi.ru/predmet/fizika/reshebnik-po-fizike-metodichka-prokofeva

10102_bgtu06_k1t1_v1

1 Определите скорость и полное ускорение а точки в момент времени t = 2 с, если она движется по окружности радиусом R = 1 м согласно уравнению s = At + Bt 3, где А = 8 м/с; В = − 1 м/с3; s − криволинейная, т. е. дуговая координата, отсчитанная вдоль дуги окружности от некоторой точки на траектории, принятой за начальную.

21 На обод маховика диаметром d = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определите осевой момент инерции Ix маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t 1 = 3 с приобрел угловую скорость 1 = 9 рад/с.

41. Горизонтальная платформа массой m 1 = 120 кг вращается с частотой n 1 = 6 об/мин. Человек массой m 2 = 80 кг стоит на краю платформы. С какой частотой п2 начнет вращаться платформа, если человек перейдет в ее центр? Платформу принять за однородный диск, а человека считайте материальной точкой.

51 Найдите скорость течения углекислого газа по трубе, если известно, что за время t = 30 мин через поперечное сечение трубы протекает газ массой m = 0,51 кг. Плотность газа = 7,5 кг/м3, диаметр трубы d = 2 см. Газ считать идеальным, несжимаемым.

61 Определите возвращающую силу F 1 в момент времени t 1 = = 0,25 с и полную энергию Е1 точки массой m = 20 г, совершающей гармонические колебания согласно уравнению x = A sin t, где A = = 15 см; = 4 с−1.

71 Твердое тело замедленно вращается вокруг неподвижной оси с угловым ускорением k, где k − положительная постоянная; − угловая скорость. В начальный момент времени его угловая скорость 0. Найдите среднюю угловую скорость за время, в течение которого тело будет вращаться.

81 Коэффициенты сжимаемости k ртути, воды и воздуха соответственно равны 3·10−10 Па−1; 5·10−10 Па−1 и 0,71·10−5 Па−1, а

плотности − 13,6 г/см 3; 1 г/см 3 и 1,2·10−3г/см3. Определите скорости звуковых волн в этих средах.

91 Свободный электрон, пройдя определенную ускоряющую разность потенциалов, движется вдоль оси х с постоянной скоростью, равной 1% от скорости света в вакууме. Определите его корпускулярные (m, p, E, К) и волновые (, k и) характеристики. Пользуясь формулой Эйлера (e− i = cos − i sin), запишите выражения для действительной 1 и мнимой 2 частей волновой функции = 1 + i 2 этого электрона. Чему будет равна дебройлевская длина волны, если скорость электрона станет равной

90% от скорости света?

10103_bgtu06_k1t1_v2

2 По прямой линии движутся две материальные точки согласно уравнениям: x 1 = A 1 + B 1 t + C 1 t 2 и x 2 = A 2 + B 2 t + C 2 t 2, где A 1 = 10 м; B 1 == 1 м/с; C 1 = 2 м/с2; A 2 = 3 м; B 2 = 2 м/с; C 2 = 1 м/с2. В какой момент времени скорости этих точек будут одинаковы? Найдите ускорения a 1 и a 2 этих точек

22. Нить с привязанными к ее концам грузами массой m 1 = 50 г и m 2 = 60 г перекинута через блок диаметром d = 4 см. Определите осевой момент инерции блока, если он вращается с угловым ускорением = 1,5 рад/с2.

42 Тонкий стержень длиной 0,5 м и массой 1 кг вращается вокруг вертикальной оси, проходящей через центр масс стержня. Симметрично оси вращения на расстоянии d = 10 см от нее на стержне расположены два небольших груза массой по m = 0,2 кг каждый.

Угловая скорость вращения 1 = 2 рад/с. Чему будет равна угловая скорость 2, если под действием внутренних сил грузы переместить на концы стержня?

52 В дне цилиндрического сосуда диаметром D = 0,5 м имеется малое круглое отверстие диаметром d = 1 см. Найдите зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найдите значение этой скорости для высоты h = 0,2 м. Примите во внимание, что при D d скорость будет много меньше, чем скорость вытекания воды из малого отверстия

62 Определите период Т0 колебаний стержня массой m длиной l = 30 см вокруг горизонтальной оси, перпендикулярной стержню и проходящей через его конец.

72 Пуля, пробив доску толщиной h, изменила свою скорость от 0 до Найдите время Т движения пули в доске, считая силу сопротивления пропорциональной квадрату скорости пули.

82. Определите скорости продольных и поперечных упругих волн в золоте. Плотность золота = 19,3 г/см3, модуль Юнга Е =

= 7,8·1010Па, модуль сдвига G = 2,7·1010Па.

92 Свободный протон, пройдя определенную ускоряющую разность потенциалов, движется вдоль оси х с постоянной скоростью, равной 5% от скорости света в вакууме. Определите его корпускулярные (m, p, К, E) и волновые (, k и) характеристики. Пользуясь формулой), запишите выражения для действительной 1 и мнимой 2 частей волновой функции = этого электрона. Как изменится дебройлевская длина волны,

если скорость протона станет равной 95% от скорости света?

10104_bgtu06_k1t1_v3

3 Точка движется по окружности радиусом R = 9 м. В некоторый момент времени нормальное ускорение an точки равно 4 м/с2, вектор полного ускорения a образует в этот момент с вектором нормального ускорения an угол = 60°. Найдите cкорость и тангенциальное ускорение a точки.

.23 Стержень массой m = 0,3 кг и длиной l = 40 см вращается вокруг оси, проходящей через его середину согласно уравнению = At + Bt 3, где В = 0,2 рад/с3. Определите вращающий момент М,

действующий на стержень в момент времени t 1 = 2 с.

43 Вертикально расположенный стержень массой m = 2 кг и длиной l = 1 м может вращаться вокруг горизонтальной оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой m 2 = 10 г, летящая перпендикулярно оси и стержню со скоростью = 500 м/с. Определите угловую скорость, с которой начнет вращаться стержень, если пуля застрянет в нем.

53 В сосуд льется вода, причем за единицу времени наливается объем воды V1 = 0,2 л/с. Каким должен быть диаметр d малого отверстия в дне широкого сосуда, чтобы вода в нем поддерживалась на постоянном уровне h = 8,3 см?

63 Определите максимальное ускорение a max материальной точки, совершающей гармонические колебания с амплитудой А = 15

см, если наибольшая скорость точки max = 30 см/с.

наименьшим усил передвигать его

волоком по горизонтальной поверхности с

заданным постоянным ускорением а (рис. 15)? Коэффициент трения

равен. Чему равна при этом сила F, т. е. ее минимальное возможное значение?

.83 В однородной среде распространяется плоская упругая волна, описываемая уравнением s = a exp(− x) cos(t − kx). Положив длину волны = 0,1 м и = 0,1 м−1, найдите разность фаз в точках, для которых отношение амплитуд А смещения частиц среды = = А1 /А2 = 1,01.

93 Электрон находится в бесконечно глубокой потенциальной яме шириной L = 0,1 нм. Получите выражение для плотности вероят-

ности f того, что электрон в основном энергетическом состоянии (n =

= 1) имеет координату х. Постройте график функции f = f (x) в

интервале 0 x L. При каком значении n энергия электрона в потенциальной яме будет равна его энергии покоя?

10105_bgtu06_k1t1_v4

4. Точка движется по прямой согласно уравнению x = At + Bt 3,

где А = 6 м/с; В = − 0,125 м/с3. Определите среднюю путевую скорость

á срñ точки в интервале времени от t 1 = 2 с до t 2 = 6 с.

24 По горизонтальной плоской поверхности катится без скольжения диск со скоростью 0 = 8 м/с. Определите эффективный коэффициент силы сопротивления (F c = N), приложенной к центру диска, если он, будучи предоставленным самому себе, остановился, пройдя равнозамедленно путь s = 18 м.

44. Вертикально расположенный стержень длиной l = 1 м и массой m 1 = 1 кг может вращаться вокруг горизонтальной оси, проходящей через его верхний конец. В другой конец стержня попадает летящая горизонтальная пуля массой m 2 = 5 г и застревает в нем. Найдите первоначальную кинетическую энергию пули, если стержень отклонился на 60°.

54 Какое давление p создает компрессор в краскопульте, если струя жидкой краски вытекает из него через малое отверстие со скоростью = 25 м/с? Плотность краски = 0,8·10 3кг/м3.

64. Точка совершает гармонические колебания, уравнение которых x = A sin t, где А = 40 см; 0 = 2 с−1. В момент времени t 1,когда на точку действовала возвращающая сила F 1 = 5 мН, точка имела потенциальную энергию П1 = 0,1 мДж. Найдите этот момент времени t 1.

. 74 Цепочка массой m = 1 кг и длиной l = 14 м висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найдите полный импульс р, который она передала столу.

84 Покоящийся источник испускает по всем направлениям

звуковую волну с длиной, равной 0. Как изменится длина волны, регистрируемая неподвижным приемником, если источник привести в движение в направлении к приемнику со скоростью, равной половине скорости звука?

94 Электрон находится в бесконечно глубокой потенциальной яме шириной L = 0,2 нм. Получите выражение для плотности вероятности f того, что электрон в первом возбужденном энергетическом состоянии (n = 2) имеет координату х. Постройте

график функции f = f (x) в интервале 0 x L. При каком значении

энергия электрона в потенциальной яме будет равна половине его энергии покоя?

10106_bgtu06_k1t1_v5

5 Материальная точка движется прямолинейно. Уравнение движения имеет вид x = At + Bt 3, где А = 3 м/с; В = 0,06 м/с3. Найдите скорость и ускорение а точки в моменты времени t 1 = 0 и t 2 = 3 с. Каковы средние значения скорости á срñ и ускорения á a срñ за первые 3 с движения?

25 Определите момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n 0 = 12 с−1, чтобы он при равнозамедленном торможении остановился в течение времени t = = 8 с. Диаметр блока d = 30 см. Массу блока m = 6 кг считать равномерно распределенной по ободу.

45. Вертикально расположенный стержень длиной l = 1 м и массой m 1 = 5 кг может вращаться вокруг горизонтальной оси, проходящей через его верхний конец. В другой конец стержня попадает пуля массой m 2 = 5 г, летящая со скоростью = 500 м/с перпендикулярно оси и стержню, и застревает в нем. Определите угловую скорость 1 стержня после попадания в него пули.

. 55 По горизонтальному участку трубы АВ течет жидкость (рис.В трубках а и b разность уровней этой жидкости h = 10 см. Диаметры трубок а и b одинаковы. Найдите скорость течения жидкости в трубе АВ.

65. Определите частоту 0 гармонических колебаний диска с радиусом R = 20 см относительно горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости

75 Какую работу нужно совершить, чтобы длинную доску, лежащую на земле, повернуть в горизонтальной плоскости вокруг одного из концов на угол? Длина доски l, масса m, коэффициент трения между доской и землей.

.85 По прямому шоссе едет со скоростью 1 = 60 км/ч легковой автомобиль. Его догоняет движущаяся со скоростью 2 = 90 км/ч спе- циальная автомашина с включенным звуковым сигналом частоты 0 = = 1 кГц. Сигнал какой частоты будут слышать пассажиры автомобиля? Скорость звука считать равной 340 м/с.

95. Протон находится в бесконечно глубокой потенциальной яме шириной L = 0,1 нм. Получите выражение для плотности вероят- ности f того, что электрон в основном энергетическом состоянии (n == 1) имеет координату х. Постройте график функции f = f (x) в интервале 0 x L. При каком значении n энергия протона в потенциальной яме будет равна его энергии покоя?

10107_bgtu06_k1t1_v6

6 Диск радиусом R = 0,2 м вращается согласно уравнению = = A + Bt + Ct 3, где А = 3 рад; В = − 1 рад/с; С = 0,1 рад/с3. Определите

тангенциальное а, нормальное an и полное а ускорения точек на ободе диска для момента времени t 1 = 10 с.

26 Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием сил натяжения нити, к концам которой подвешены грузы массами m 1 = 0,3 кг и m 2 = 0,7 кг. Определите силы T 1 и T 2 натяжения нити по обе стороны блока.

46. Горизонтально расположенный деревянный стержень массой m 1 = 0,8 кг и длиной l = 1, 8 м может вращаться вокруг перпендикулярной к нему вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массой m 2

= 3 г, летящая перпендикулярно к оси и к стержню со скоростью 2 = 50 м/с. Определите угловую скорость, с которой начинает вращаться стержень.

56. Насосная станция города поддерживает в трубах водопровода на уровне первого этажа давление 5 атм. Определите 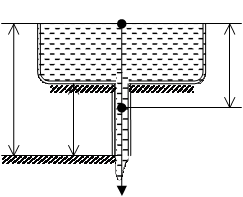(пренебрегая трением при течении O жидкости) скорость струи воды, вытекающей из крана на первом, втором и третьем этажах, если краны каждого последующего этажа А расположены на 4 м выше. На какой этаж вода по водопроводу уже не поднимется?

66 Определите период Т0 гармонических колебаний диска радиусом R = 40 см относительно горизонтальной оси, проходящей через образующую диска.

76. Определите минимальную работу, которую нужно затратить, чтобы насыпать из песка (набирая его малыми порциями с поверхности земли) конус, радиус которого R = 12 м, а высота h = 10 м. Плотность песка = 2·103кг/м3.

86 Определите уровень громкости звука L = lg (I / I 0), создаваемого в воздухе упругой волной s = А cos(t − kx), где A = 1·10−4м; == 6280 с−1; k = 18,5 м−1. Интенсивность I 0, соответствующая порогу слышимости, равна 10−12 Вт/м2; плотность воздуха = 1,29 кг/м3.

96 Протон находится в бесконечно глубокой потенциальной яме шириной L = 0,2 нм. Получите выражение для плотности вероятности f того, что электрон в первом возбужденном энергетическом состоянии (n = 2) имеет координату х. Постройте график функции f = f (x) в интервале 0 x L. При каком значении n энергия протона в потенциальной яме будет равна половине его энергии покоя?

10108_bgtu06_k1t1_v7

.7 Скорость точки, движущейся по окружности радиусом 4 м, изменяется по закону = At + Bt 2, где А = 1 м/с2; В = 3 м/с3. Найдите: 1) путь, пройденный точкой за 6 с после начала движения; 2) тангенциальное и полное ускорения точки в момент времени t 1 = 1 с.

.27 К ободу однородного сплошного диска массой m = 10 кг, насаженного на ось, приложена касательная сила F = 30 Н. Определите радиус R диска, если через время t 1 = 4 с после начала действия силы угловая скорость 1 стала равной 240 рад/с.

47. Решите предыдущую задачу, заменив пулю пластмассовым шариком той же массы и движущимся с той же скоростью. Удар считайте абсолютно упругим. Определите угловую скорость стержня и скорость и шарика сразу же после удара.

57. Сосуд с водой подвешен к потолку. Высота воды в сосуде h. На сколько изменится натяжение подвеса, если в днище сосуда открыть маленькое отверстие, из которого вытекает струя с поперечным сечением S? Плотность воды.

67 На невесомом стержне длиной l = 30 см укреплены два одинаковых груза: один в середине стержня, другой − на одном из его концов. Стержень с грузами колеблется относительно горизонтальной оси, проходящей через свободный конец стержня. Определите приведенную длину l пр маятника и период Т0 гармонических колебаний.

.77 Какую минимальную работу А требуется совершить, чтобы вырыть прямоугольную яму площадью основания S и глубиной H, считая, что выбираемый из ямы малыми порциями грунт поднимается до уровня H = 0. Плотность грунта.

87 Упругая волна s = A cos (t − x /) распространяется в воде. Определите среднее значение плотности энергии волны и волновой поток энергии через отверстие площадью S в экране, установленном параллельно плоскому фронту волны (S = 0,3 м3). Амплитуда A = = 10−4 м; частота = 103 Гц; длина волны = 1,48 м.

97 Электрон как квантовый осциллятор с частотой 0 = 5·1014Гц находится в основном, т. е. невозбужденном, состоянии. Получите выражение для плотности вероятности f того, что он имеет координату х. При вычислении нормировочной постоянной А0

10109_bgtu06_k1t1_v8

8 Найдите линейную скорость и нормальное ускорение точек поверхности Земли в ее суточном вращении на широте Минска (= = 54°, cos 54° = 0,5878). Радиус Земли принять равным 6400 км.

28 К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 100 Н. При вращении диска на него действует момент сил трения Мтр = 2 Н·м. Определите

массу m диска, если известно, что его угловое ускорение постоянно и равно = 16 рад/с2.

48 На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек. Масса платформы М = 200 кг, масса человека m = 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найдите, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью u = 2 м/с относительно платформы.

58 Из широкого сосуда через узкую цилиндрическую трубку длиной h вытекает несжимаемая жидкость плотности (рис. 14). Как зависит давление р и скорость жидкости в сосуде и трубке от положения точки А с координатой х? Давление воздуха p 0.

68 Найдите максимальную кинетическую энергию Кmax

материальной точки массой m = 2 г, совершающей гармонические колебания с амплитудой А = 4 см и частотой = 5 Гц.

.78 Маховик, масса которого 6 кг равномерно распределена по ободу радиусом 18 см, вращается на валу с частотой п0 = 600 мин−1. Под действием тормозящего момента М = 10 + 0,1 (в Н·м) маховик останавливается. Найдите зависимость угловой скорости и время

торможения.

88. Волновой пакет состоит из двух поверхностных волн на воде, которые распространяются в одном направлении с близкими фазовыми скоростями (1 = 24 см/с; 2 = 25 м/с). Их волновые числа k 1

и k 2 равны 3,92 см−1 и 3,69 см−1 соответственно. Рассчитайте групповую скорость этого пакета, используя средние значения фазовой скорости и длины волны

98 Протон как квантовый осциллятор с частотой 0 = 5·1014Гц находится в основном, т. е. невозбужденном, состоянии. Получите выражение для плотности вероятности f того,чтоон имеет координату х. При вычислении нормировочной постоянной А0

10110_bgtu06_k1t1_v9

9. Свободно падающее тело в последнюю секунду движения проходит половину всего пути. С какой высоты падает тело и каково время t 1 его падения?

29. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите осевой момент инерции барабана, если известно, что груз опускается с ускорением а =

2,04 м/с2.

49. На скамье Жуковского стоит человек и держит в руках стержень, расположенный вертикально по оси вращения скамейки. Скамья с человеком вращается с угловой скоростью 1 = 1 рад/с. С какой угловой скоростью 2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный осевой момент инерции человека и скамейки I = 6 кг·м2. Длина стержня l = 2,4 м, его масса m = 8 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.

.59 Бак с площадью основания S 1 = 10 м 2 и объемом 100 м 3

заполнен водой. Пренебрегая вязкостью воды, определите время Т, необходимое для полного опустошения бака, если на дне бака образовалось малое отверстие площадью S 2 = 8 см 2.

69 Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x = A 1 sin 1 t и y = A 2 cos 2 t, где А1 = 8 см; А2 = 4 см; 1 = 2 = 2 с−1. Получите уравнение траектории и постройте ее на чертеже; укажите направление движения точки по этой траектории.

79. Стержень длиной l = 50 см совершает колебания относительно горизонтальной оси, проходящей через точку О, находящуюся на расстоянии b от центра масс стержня. Определите период колебаний стержня как функцию от расстояния b, а затем найдите минимальное значение периода Т0 и соответствующее ему значение b 0.

89. Плоская волна распространяется вдоль прямой со скоростью

= 25 м/с. Период колебаний Т = 0,02 с. Запишите уравнение этой волны и найдите разность фаз колебаний двух точек среды, находящихся на указанной прямой на расстоянии х = 30 см друг от друга.

99. Электрон как квантовая частица с энергией Е = 1,5 эВ движется навстречу прямоугольному потенциальному барьеру высотой U 0 = 1,2 эВ и шириной L = 0,1 нм. Рассчитайте коэффициент прозрачности D и поясните его физический смысл. Определите дебройлевскую длину волны этого электрона. Во сколько раз энергия покоя электрона отличается от заданной энергии Е?

10111_bgtu06_k1t1_v10

10. Найдите угловое ускорение колеса, если известно, что через время t 1 = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол = 60° с вектором ее линейной скорости.

30. Вентилятор вращается с частотой n 0 = 10 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Найдите осевой момент инерции вентилятора, если момент сил торможения равен 9,4·10−2Н·м. 50. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n 1 = 8 мин−1, стоит человек массой m 1 = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n 2 = 10 мин−1. Определите массу m 2 платформы. Момент инерции человека рассчитывать как для материальной точки.

60. Бак высотой Н = 1,5 м наполнен до краев водой. На расстоянии h = 1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии b от бака падает на пол струя, вытекающая из отверстия?

70. Складываются два колебания одинакового направления и одинакового периода: x 1 = A 1 sin 1 t и x 2 = A 1 sin 2(t +), где А1 = А2 = = 3 см; 1 = 2 = с−1; = 0,5 с. Определите амплитуду А и начальную фазу 0 результирующего колебания. Напишите его уравнение.

80. Используя выражение для амплитуды А вынужденных колебаний (см. формулу (1.65)), зависящей от частоты р вынуждающей внешней периодической силы, определите ее максимальное значение. Как называется частота колебаний с максимально возможной амплитудой?

90. Уравнение плоской волны, распространяющейся в упругой среде, имеет вид s = 1·10−8sin(6280 t − 1,256 x). Определите длину волны, скорость ее распространения и плотность w энергии.

100. Протон как квантовая частица с энергией Е = 1,3 эВ движется навстречу прямоугольному потенциальному барьеру высотой U 0 = 1,5 эВ и шириной L = 0,1 нм. Рассчитайте коэффициент прозрачности D и поясните его физический смысл. Определите дебройлевскую длину волны этого протона. Во сколько раз энергия покоя протона отличается от заданной энергии Е?

Поиск по сайту: