 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Габец БГУИр 1997 До
| Вариант | НОМЕРА ЗАДАЧ | |||||||||
201. Частица совершает гармонические колебания амплитуды А и периода Т. Найти время, за которое смещение частицы изменяется от 0 до А/4.
202. Черва сколько времени от начала движения точка, совершающая колебательное движение, согласно уравнению х = 7sin0,5p t, проходит путь от положения равновесия до максимального смещения.
203. Частица совершает колебания вдоль оси х по закону х = 6cos0,5(t+l) см. Найти путь, пройденный частицей за период, а также среднее значение скорости <V> за первую четверть периода.
204. Частица совершает гармонические колебания с периодом 2 с и амплитудой 4 см. Найти скорость точки в момент времени, когда смещение частицы равно 2 см.
205. Найти период Т и амплитуду А гармонических колебаний частицы, если при смещениях x1 и х2 от положения равновесия скорости равны соответственно V1 и V2
206. Точка совершает гармонические колебания по закону х = Acosw t. В некоторый момент времени смещение равно 5 см; когда фаза колебаний увеличилась вдвое, смещение стало равным 8 см. Найти амплитуду А колебаний.
207. Газ совершает цикл Карно, абсолютная температура нагревателя в три раза выше температуры холодильника. Какую работу выполняет гав, если он от нагревателя получает количество теплоты 90 МДж?
208. Колебания точки происходят по закону х = Acos(w t+j). В некоторый момент времени смещение точки равно 5 см, ее скорость V = 20 см/с и ускорение а = - 80 см/с2. Найти амплитуду А. циклическую частоту w, период колебаний Т и фазу (w t+j) в рассматриваемый момент времени.
209. Определить период Т колебаний математического маятника, если его модуль максимального перемещения D r = 18 см и максимальная скорость Vmax = 16 см/с.
210. Материальная точка совершает гармонические колебания так, что в начальный момент времени смещение х0 = 4 см, а скорость! V0 = 10 см/с. Определить амплитуду А и начальную фазу j 0 колебаний, если их период Т = 2 с.
211. Найти возвращающую силу в момент, t = 1 с и полную энергию частицы, совершающей колебания по закону х = Acosw t, где А = 20 см, w = 2л/3 с -1. Масса частицы m = 10 г.
212. Колебания частицы происходят согласно уравнение х = Acosw t, где А = 8 см, w = л/6 с –1. В момент времени, когда возвращающая сила в первый раз достигла значения F = -5 мН, потенциальная энергия U = 100 мкДж. Определить этот момент времени и соответствующую ему фазу (w t).
213. Шарик c m = 100 г, подвешенный кневесомой пружине с коэффициентом жесткости k = 10 Н/м, совершает гармонические колебания с амплитудой А = 4-10 -2 м. Начальная фаза равна нулю. Найти:
а) смещение шарика через t = 52,36-10 -3 с после начала колебаний;
б) полную энергию шарика и его кинетическую энергию в момент прохождения им положения равновесия.
214. Маятник состоит из шарика с m = 100 г, подвешенного на нити длиной 0,5 м. Определить энергию маятника, если наибольший угол отклонения равен 15°.
215. Уравнение колебаний частицы массой 1.6-10 -2 кг имеет вид х = 0,lsln(p t/8 + л/4) (м). Построить график зависимости от времени силы F, действующей на частицу. Найти значение максимальной силы.
216. Частица m = 10 г колеблется согласно уравнению х =5sln(p t/5 + л/4) (см). Найти максимальную силу, действующую на частицу и полную энергию колебаний.
217. Найти отношение кинетической энергии точки совершающей гармонические колебания, к ее потенциальной энергии для моментов времени: 1) t = Т/12 с; 2) t = Т/8 с. Начальная фаза колебаний равна нулю.
218. Полная энергия тела, совершающего гармонические колебания, равна 3-10 -5 Дж. максимальная сила, действующая на тело, равна 1,5-10 -3 Н. Написать уравнение движения этого тела, если период колебаний равен 2 с и начальная фаза 60°.
219. Найти возвращающую силу F в момент t = 1 с и полную энергию Е точки, совершающей колебания по закону х = Acos(w t, где А = 20 см; w = 2p /3 с -1. Масса m = 10 г.
220. Амплитуда гармонических колебаний частицы А = 2 см, полная энергия колебаний Е = 3-10 -7 Дж. При каком смешении от положения равновесия на точку действует сила F = 2,25-10 -5 Н?
221. Определить период колебаний стержня длиной 20 см около горизонтальной оси, перпендикулярной стержню и проходящей через его конец.
222 Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стенку, колеблется в плоскости, параллельной стенке. Радиус обруча равен 20 см. Найти период колебаний обруча.
223. Диск радиусом 20 см колеблется около горизонтальной оси, походящей через середину радиуса перпендикулярно плоскости диска. Определить приведенную длину и период колебаний.
224. Тонкий стержень длиной 1 м свободно вращается вокруг горизонтальной оси, отстоящей на х = 20 см от его середины. Определить период колебаний стержня. Построить график зависимости Т(х).
225. На стержне длиной 40 см укреплены два одинаковых грузика: один в середине стержня, другой на одном из его концов. Определить период колебаний стержня относительно горизонтальной оси, проходящей через свободный конец стержня. Масса стержня М, а грузиков - m.
226. Стержень длиной 60 см колеблется около горизонтальной оси, проходящей через его конец. Во сколько раз изменится период колебаний, если точку подвеса сдвинуть на 10 см от конца стержня?
227. Шар массой М и радиусом R подвешен на стержне длиной l и массой m в точке, лежащей на поверхности шара. Определить период колебания системы.
228. Физический маятник в виде тонкого прямого стержня длиной 120 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние L от центра масс стержня. При каком значении L период Т колебаний имеет наименьшее значение?
229. Тело массой 5 кг, закрепленное на горизонтальной оси, совершало колебания с периодом Т = 0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период колебаний стал равным 1,2 с. Радиус диска равен 24 см, масса его равна массе тела. Найти момент инерции тела относительно оси колебаний.
230. Определить период Т гармонических колебаний диска радиусом 40 см около горизонтальной оси, проходящей черев образующую диска.
231. Найти число полных колебаний системы, если период собственных колебаний системы равен 1с, а логарифмический декремент А = 0,01.
232. Продольная волна с частотой 262 Гц имеет скорость в воздухе 345 м/с. Найти длину волны и время, за которое фaзa в данной точке меняется на 90°, а также разность фаз (в градусах) между точками, отстоящими друг от друга на 6,4 см.
233. От источника колебаний распространяется волна вдоль оси х. Амплитуда А колебаний равна 10 см. Найти точку, удаленную от источника на х = Зl /4, в момент, когда от начала колебаний прошло время t = 0,9 Т.
234. Определить скорость, если разность фаз D j колебаний двух точек среды, отстоящих друг от друга на D x = 10 см, равна p /З. Частота колебаний равна 25 Гц.
235. Две точки находятся на расстоянии 50 см друг от друга на прямой, вдоль которой распространяется волна со скоростью V = 50 м/с. Период колебаний Т равен 0,05 с. Найти разность фаз D j колебаний в этих точках.
236. Найти разность фаз D j колебаний двух точек, лежащих на луче на расстоянии 2 м, если длина волны равна 1 м.
237. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии l = l /12, для момента t = Т/6. Амплитуда колебаний равна 0,05 м.
238. Смещение точки, находящейся на расстоянии 4 см от источника колебаний в момент t = Т/6, равно половине амплитуды. Найти длину бегущей волны.
239. Амплитуда затухающих колебаний маятника за 5 мин уменьшилась в 2 раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь paз?
240. За время 6 мин амплитуде затухающих колебаний уменьшилась в три раза. Определить коэффициент затухания,
241. В баллоне объемом 10 л находится аргон Определить плотность гaзa, если температура Т = 300 К, а давление р = 1 атм.
242. Определить массу неона и число молекул, если при давлении 9,8-105 Па и температуре 300 К он занимает объем 3 л.
243. Азот находился в баллоне объемом 5 л при температуре 300 К. Когда выпустили некоторое количество газа, давление изменилось на 5-104 Па. Определить массу вытекшего газа.
244. В сосуде под давлением 106 Па находится азот N2. Определить массу азота, если добавление в сосуд 2 г углекислого газа вызывает изменение давления 1,5-104 Па.
245. Вычислить плотность азота, находящегося в баллоне под давлением 2 МПа и имеющего температуру 400 К.
246. 12 г газа занимают объем 4-10 -3 м3 при температуре 7°С. После нагревания газа при постоянном давлении его плотность стала равна 6-10 -4 г/см3. До какой температуры нагрели газ?
247. В закрытом сосуде емкостью 1 м3 находятся 0,9 кг воды и 1,6 кг кислорода. Найти давление в сосуде при температуре 500°С, зная, что при этой температуре вся вода превращается в пар.
248. При изменении давления газа на 200 Па объем газа изменится на 3 л. Если давление изменить на 500 Па, объем изменится на 5 л. Найти начальный объем и давление raзa. Температура газа сохраняется постоянной.
249. В баллоне находилось некоторое количество газа при нормальном давлении. При открытом вентиле баллон был нагрет, после чего вентиль закрыли и газ остыл до температуры 283° К. При этом давление в баллоне упало до 70 кПа. На сколько градусов нагрели баллон?
250. Давление воздуха внутри закупоренной бутылки при температуре 280 К было равно 100 кПа. На сколько градусов необходимо нагреть бутылку, чтобы из нее вылетела пробка, если известно, что ив холодной бутылки без нагревания пробку можно вынуть силой 10 Н? Сечение пробки 4 см2.
251. Какая часть молекул азота при Т = 273 К обладает скоростями от V1 = 250 м/с до V2 = 225 м/с?
252. Определить отношение наиболее вероятных скоростей молекул метана NH4 и гелия, находящихся при температуре Тm = 300°К и Тг = 200°К.
253. Найти с помощью распределения Максвелла <V2x> среднее значение квадрата проекции скорости молекулы газа при температуре Т.
254. Восколько раз изменится среднеквадратичная скорость молекул газа при увеличении его температуры в 4 раза.
255. Определить среднюю квадратичную скорость молекулы газа, заключенного в сосуд объемом 2л, под давлением 200 кПа. Масса газа m = 0,3 г.
256. При какой температуре средняя кинетическая энергия поступательного движения молекулы газа равна 4,14-10 -21 Дж?
257. Средняя квадратичная скорость молекул некоторого газа равна 450 м/с. Давление газа р =25 кПа. Найти удельный объем V0 газа при этих условиях (V0 =V/m)
258. При какой температуре средняя кинетическая энергия теплового движения атомов гелия окажется достаточной для того, чтобы атомы гелия покинули атмосферу Земли?
259. Найти отношение средних квадратичных скоростей молекул водорода и кислорода при одинаковых температурах.
260. Водород находится при нормальных условиях в объеме 1 см3. Определить число молекул в этом объеме, обладающих скоростями, меньше 1 м/с.
261. Определить внутреннюю энергию кислорода массой 3 г при температуре 300°К.
262. Определить показатель адиабаты газа, если 2 моля при температуре 300°К имеют такую же внутреннюю энергию, как 50 кг гелия при температуре 400°К
263. При изотермическом расширении азота массой 0,2 кг и температурой 280 °К объем еro увеличился в два раза. Определить работу, изменение внутренней энергии и количество теплоты, полученное газом.
264. При адиабатическом сжатии давление воздуха было увеличено от 50 кПа до 0,5 МПа. Затем, при неизменном объеме, температура воздуха была понижена до первоначальной. Определить давление газа в конце процесса.
265. Найти работу, совершающуюся при изотермическом расширении водорода массой 5 г, при температуре 290°К. при увеличении объема газа в три раза.
266. 1 кг азота занимает объем 0,3 м3 под давлением 5-105 Па. Затем газ расширяется, в результате чего его объем становится равным 1м3, а давление - равным 10" Па. Определить приращение внутренней анергии газа D U. Можно ли вычислить работу, совершенную raзoм при расширении?
267. В результате обратимого изотермического (при Т = З00°К) расширения 531 г азота N2 давление газа уменьшается от 20-105 до 2-105 Па. Найти работу, совершаемую газом при расширении, и количество полученного газом тепла Q.
268. 321 г гелия находится при температуре 20°С и давлении 105 Па, затем его адиабатически сжимают до давления 107 Па. Считая процесс обратимым, определить температуру газа в конце сжатия и работу, совершаемую газом. Во сколько раз уменьшился объем газа?
269. Идеальный газ, расширяясь изотермически при 400°К, совершает работу 800 Дж. Что происходит при этом с энтропией газа?
270. При обратимом изотермическом процессе при температуре 350 К тело совершает работу 80 Дж, а внутренняя энергия тела получает приращение 7,5 Дж. Что происходит с энтропией тела?
271. В каком случае КПД цикла Карно повысится больше: при увеличении температуры нагревателя на D Т или при уменьшении температуры холодильника на ту же величину?
272. Во сколько раз увеличится КПД цикла Карно при увеличении температуры нагревателя от t1 = 300°К до T 2 = 380 К при температуре холодильника T2 = 200°К?
273. Какова полезная работа А, совершаемая в цикле Карно, если при температурах нагревателя t1 = 400°К и холодильника T2 = 300°К полученная газом теплота составляет Q = 300 Дж?
274. Газ, совершающий цикл Карно, получает теплоту 75 Дж и совершает работу 50 Дж. Определить температуру холодильника, если температура нагревателя t1 = 300°К.
275. В ходе цикла Карно рабочее вещество получает тепло 300 кДж. Температура нагревателя 450°К, холодильника - 280°К. Найти работу, совершаемую рабочим веществом за цикл.
276. Идеальная тепловая машина работает по циклу Карно. При этом 80% тепла, получаемого от нагревателя, передается холодильнику. Количество тепла, получаемое от нагревателя, равно 1,5 ккал. Найти КПД цикла и работу, совершенную при полном цикле.
277. Идеальная холодильная машина, работающая по обратному циклу Карно, совершает за один цикл работу 3,104 Дж. При этом она берет тепло от тела с температурой -10°С и передает тепло телу с
температурой +17°С. Найти КПД цикла, количество тепла, отнятого у холодного тела за один цикл.
278. Газ совершает цикл Карно, абсолютная температура нагревателя в три раза выше температуры холодильника. Какую работу выполняет гав, если он от нагревателя получает количество теплоты
90 МДж?
279. Найти КПД цикла, состоящего из двух изотерм с температурами t1 и Т2 (T1>T2) и двух изохор с объеми и V2 (Vi>V2).
280. Найти КПД цикла, состоящего из двух изотерм с температурами Т1 и Т2 (T1>T2) и двух изобар с давлениями и р2 (p1>p2).
10043_bguir11gor_v2
1.
Ускорение материальной точки изменяется по закону  , где
, где  ;
;  . Найти кинематический закон движения точки, а также модуль ее перемещения за время
. Найти кинематический закон движения точки, а также модуль ее перемещения за время  , где
, где  , если при
, если при 
 и
и  .
.
2. Частица массой m в момент  начинает двигаться под действием силы
начинает двигаться под действием силы  , где
, где  и ω – постоянные. Найти путь, пройденный частицей, в зависимости от t.
и ω – постоянные. Найти путь, пройденный частицей, в зависимости от t.
3. Тело массой  начинают поднимать с поверхности Земли под действием силы
начинают поднимать с поверхности Земли под действием силы 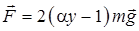 , где
, где  – положительная постоянная. Найти работу всех сил, действующих на тело на высоте
– положительная постоянная. Найти работу всех сил, действующих на тело на высоте 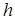 .
.
4. На гладкой наклонной плоскости, составляющей угол 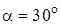 с горизонтом, находится катушка с ниткой, свободный конец которой укреплен, как показано на рис. 1.8. Масса катушки
с горизонтом, находится катушка с ниткой, свободный конец которой укреплен, как показано на рис. 1.8. Масса катушки  г, ее момент инерции относительно собственной оси
г, ее момент инерции относительно собственной оси 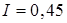 г·м2, радиус намотанного слоя ниток
г·м2, радиус намотанного слоя ниток  cм. Найти ускорение оси катушки.
cм. Найти ускорение оси катушки.
5. Через какое минимальное время  после начала колебаний смещение колеблющейся материальной точки составит половину амплитуды. Период колебаний
после начала колебаний смещение колеблющейся материальной точки составит половину амплитуды. Период колебаний  с. Найти среднюю скорость точки за это время. Амплитуда колебаний
с. Найти среднюю скорость точки за это время. Амплитуда колебаний  см,
см,  .
.
6. Водород  находится при температуре
находится при температуре  . Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также кинетическую энергию всех молекул газа, если количество вещества
. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также кинетическую энергию всех молекул газа, если количество вещества  .
.
7. Найти молярную массу газа, если при нагревании  кг этого газа на
кг этого газа на  изобарически требуется на
изобарически требуется на  кДж тепла больше, чем при изохорическом нагревании.
кДж тепла больше, чем при изохорическом нагревании.
8.. Идеальный газ, совершающий цикл Карно, получает теплоту  . Определить работу газа, если температура нагревателя
. Определить работу газа, если температура нагревателя  в 2 раза выше температуры холодильника
в 2 раза выше температуры холодильника  .
.
10044_bguir11gor_v3
Скорость материальной точки, движущейся в плоскости ХУ, изменяется со временем по закону  , где
, где  и
и  – положительные постоянные. Найти: 1) зависимость от времени модуля скорости и ускорения точки; 2) зависимость от времени радиуса-вектора точки; 3) модуль радиуса-вектора точки в момент времени
– положительные постоянные. Найти: 1) зависимость от времени модуля скорости и ускорения точки; 2) зависимость от времени радиуса-вектора точки; 3) модуль радиуса-вектора точки в момент времени  . В момент
. В момент  радиус-вектор точки равен нулю.
радиус-вектор точки равен нулю.
В момент  частица массой m начинает двигаться под действием силы
частица массой m начинает двигаться под действием силы  , где
, где  и ω – постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время?
и ω – постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время?
Тело массой  бросили под углом
бросили под углом  к горизонту с начальной скоростью
к горизонту с начальной скоростью  . Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.
. Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.
Однородный шар скатывается без скольжения по наклонной плоскости, составляющей угол  с горизонтом. Найти ускорение центра шара и значение коэффициента трения качения.
с горизонтом. Найти ускорение центра шара и значение коэффициента трения качения.
Частица совершает гармонические колебания вдоль оси Х из положения равновесия. Циклическая частота колебаний частицы  рад/с. Найти момент времени
рад/с. Найти момент времени  после начала движения, когда частица первый раз окажется в точке с координатой
после начала движения, когда частица первый раз окажется в точке с координатой 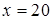 см, со скоростью
см, со скоростью  м/с.
м/с.
53. Азот  находится при температуре
находится при температуре  . Определить среднюю кинетическую энергию поступательного и вращательного движения одной молекулы, а также ее среднюю квадратичную скорость
. Определить среднюю кинетическую энергию поступательного и вращательного движения одной молекулы, а также ее среднюю квадратичную скорость
63Один моль некоторого идеального газа изобарически нагрели на  К, сообщив ему количество тепла
К, сообщив ему количество тепла 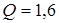 кДж. Найти приращение его внутренней энергии и величину
кДж. Найти приращение его внутренней энергии и величину  .
.
Идеальный газ совершает цикл Карно. Определить температуру холодильника  и КПД цикла, если теплота, полученная газом за цикл, в 4 раза больше совершенной им работы. Температура нагревателя
и КПД цикла, если теплота, полученная газом за цикл, в 4 раза больше совершенной им работы. Температура нагревателя 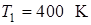 .
.
10045_bguir11gor_v4
1. Точка движется в плоскости ХУ по закону  ,
,  , где
, где  и
и 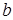 – положительные постоянные. Найти: 1) уравнение траектории точки
– положительные постоянные. Найти: 1) уравнение траектории точки  , изобразить ее график; 2) зависимость от времени модуля скорости и ускорения точки; 3) зависимость от времени угла
, изобразить ее график; 2) зависимость от времени модуля скорости и ускорения точки; 3) зависимость от времени угла  между векторами скорости и ускорения.
между векторами скорости и ускорения.
2. Катер массой m движется по озеру со скоростью  . В момент
. В момент  выключили его двигатель. Считая силу сопротивления пропорциональной скорости катера,
выключили его двигатель. Считая силу сопротивления пропорциональной скорости катера,  ,
,  , найти: 1) время движения катера с выключенным двигателем; 2) скорость катера в зависимости от пути, пройденного с выключенным двигателем; 3) полный путь до остановки.
, найти: 1) время движения катера с выключенным двигателем; 2) скорость катера в зависимости от пути, пройденного с выключенным двигателем; 3) полный путь до остановки.
3. Частица массой  движется по окружности радиусом
движется по окружности радиусом  с нормальным ускорением, которое меняется со временем по закону
с нормальным ускорением, которое меняется со временем по закону  , где
, где  – постоянная. Найти зависимость от времени мощности всех сил, действующих на частицу, а также среднее значение этой мощности за первые
– постоянная. Найти зависимость от времени мощности всех сил, действующих на частицу, а также среднее значение этой мощности за первые  секунд после начала движения.
секунд после начала движения.
4. 4 Однородный шар массой  кг скатывается без скольжения по наклонной плоскости, составляющей угол
кг скатывается без скольжения по наклонной плоскости, составляющей угол 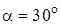 с горизонтом. Найти кинетическую энергию шара через
с горизонтом. Найти кинетическую энергию шара через  с после начала движения.
с после начала движения.
5. Пружинный маятник вывели из положения равновесия и отпустили. Через какое минимальное время  , считая от начала колебания, его потенциальная энергия станет равна кинетической, если масса маятника
, считая от начала колебания, его потенциальная энергия станет равна кинетической, если масса маятника  г, а жесткость пружины
г, а жесткость пружины 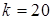 Н/м?
Н/м?
6. 54. Определить среднюю квадратичную скорость молекулы газа, масса которого  заключена в сосуде объемом
заключена в сосуде объемом  под давлением
под давлением  .
.
1. 64. Водород  занимает объем
занимает объем  м3 при давлении
м3 при давлении  МПа. Его нагрели при постоянном объеме до давления
МПа. Его нагрели при постоянном объеме до давления  МПа. Определить изменение
МПа. Определить изменение  внутренней энергии водорода, работу
внутренней энергии водорода, работу  , совершенную им, и теплоту
, совершенную им, и теплоту  , сообщенную газу.
, сообщенную газу.
2. 74. Идеальный газ совершает цикл Карно. Температура нагревателя 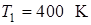 , температура холодильника
, температура холодильника  . Определить КПД цикла, а также работу газа при изотермическом расширении, если при изотермическом сжатии совершена работа
. Определить КПД цикла, а также работу газа при изотермическом расширении, если при изотермическом сжатии совершена работа  .
.
10046_bguir11gor_v5
Точка движется в плоскости ХУ по закону  ,
, 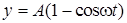 , где А и ω – положительные постоянные. Найти: 1) скорость и ускорение точки в зависимости от времени; 2) путь s, проходимый точкой за время
, где А и ω – положительные постоянные. Найти: 1) скорость и ускорение точки в зависимости от времени; 2) путь s, проходимый точкой за время  .
.
К бруску массой  , лежащему на гладкой горизонтальной плоскости, приложили постоянную по модулю силу
, лежащему на гладкой горизонтальной плоскости, приложили постоянную по модулю силу  . В процессе его прямолинейного движения угол
. В процессе его прямолинейного движения угол  между направлением этой силы и горизонтом меняют по закону
между направлением этой силы и горизонтом меняют по закону  , где
, где  – постоянная,
– постоянная,  – пройденный бруском путь (из начального положения). Найти скорость бруска как функцию угла
– пройденный бруском путь (из начального положения). Найти скорость бруска как функцию угла  .
.
В результате упругого центрального столкновения частицы 1 массой  с покоившейся частицей 2 обе частицы разлетелись в противоположных направлениях с одинаковыми скоростями. Найти массу частицы 2.
с покоившейся частицей 2 обе частицы разлетелись в противоположных направлениях с одинаковыми скоростями. Найти массу частицы 2.
 На ступенчатый вал, радиусы которого
На ступенчатый вал, радиусы которого  и
и  , намотаны нити, нагруженные одинаковыми массами
, намотаны нити, нагруженные одинаковыми массами  (рис. 1.9). Момент инерции вала
(рис. 1.9). Момент инерции вала  . Массой нити и трением в оси блока пренебречь. Найти ускорение
. Массой нити и трением в оси блока пренебречь. Найти ускорение 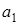 и
и  грузов.
грузов.
Частица совершает колебания вдоль оси 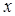 по закону
по закону  . Найти путь, пройденный частицей за период, а также среднее значение скорости
. Найти путь, пройденный частицей за период, а также среднее значение скорости  и среднее значение ускорения
и среднее значение ускорения 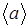 за первую четверть периода.
за первую четверть периода.
.55
Определить среднюю квадратичную скорость и среднюю кинетическую энергию поступательного движения молекулы кислорода 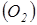 , находящегося при температуре
, находящегося при температуре  .
.
Кислород  нагревают при постоянном давлении
нагревают при постоянном давлении  . Его объем увеличивается от
. Его объем увеличивается от  до
до  . Определить изменение
. Определить изменение  внутренней энергии кислорода, работу
внутренней энергии кислорода, работу  , совершенную газом при расширении, а также теплоту
, совершенную газом при расширении, а также теплоту  , сообщенную кислороду при нагревании.
, сообщенную кислороду при нагревании.
Идеальный газ совершает цикл Карно. Определить температуру  нагревателя, если за один цикл газ отдает холодильнику
нагревателя, если за один цикл газ отдает холодильнику  , а при температуре холодильника
, а при температуре холодильника  работа цикла
работа цикла  .
.
10046_bguir11gor_v9
Колесо вращается вокруг неподвижной оси так, что угол  его поворота зависит от времени, как
его поворота зависит от времени, как  , где
, где  рад/с2. Найти полное ускорение а точки А на ободе колеса в момент
рад/с2. Найти полное ускорение а точки А на ободе колеса в момент  c, если скорость точки А в этот момент
c, если скорость точки А в этот момент  м/с.
м/с.
Частица массой  г движется из начала координат прямолинейно вдоль оси Х под действием силы
г движется из начала координат прямолинейно вдоль оси Х под действием силы 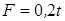 . Найти кинематический закон движения частицы и ее координату в момент времени
. Найти кинематический закон движения частицы и ее координату в момент времени  с. В начальный момент времени скорость частицы была равна 1 м/с.
с. В начальный момент времени скорость частицы была равна 1 м/с.
Пуля массой 20 г, летящая со скоростью 300 м/с, застревает в нижнем конце вертикального стержня длиной 1 м и массой 2 кг, который может вращаться вокруг горизонтальной оси, проходящей через верхний конец. Найти угловую скорость стержня сразу после попадания пули и его кинетическую энергию.
По горизонтальной плоскости катится однородный диск с начальной скоростью  м/с. Определить коэффициент трения между плоскостью и диском, если диск, будучи предоставленным самому себе, остановится, пройдя путь
м/с. Определить коэффициент трения между плоскостью и диском, если диск, будучи предоставленным самому себе, остановится, пройдя путь 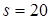 м.
м.
Материальная точка совершает гармонические колебания так, что в начальный момент времени ее смещение  см, а скорость
см, а скорость  см/с. Определить амплитуду
см/с. Определить амплитуду  и начальную фазу
и начальную фазу  колебаний точки, если ее период
колебаний точки, если ее период  с.
с.
59. Определить внутреннюю энергию 1 моля водорода  и среднюю кинетическую энергию молекулы водорода, если газ находитсяпри температуре
и среднюю кинетическую энергию молекулы водорода, если газ находитсяпри температуре  .
.
69. Азот  массой
массой  изобарно нагревают от температуры
изобарно нагревают от температуры  до температуры
до температуры  . Определить изменение внутренней энергии азота
. Определить изменение внутренней энергии азота  , работу
, работу  , совершенную газом, и полученную им теплоту
, совершенную газом, и полученную им теплоту  в этом процессе.
в этом процессе.
79. Тепловой двигатель работает по циклу Карно. За цикл двигатель совершает работу  и 70 % теплоты, полученной от нагревателя, отдает холодильнику. Найти КПД цикла и количество теплоты
и 70 % теплоты, полученной от нагревателя, отдает холодильнику. Найти КПД цикла и количество теплоты  , полученной двигателем от нагревателя.
, полученной двигателем от нагревателя.
10047_bntu_120_v1
101.Материальная точка движется прямолинейно. Уравнение движения имеет вид: S = 2t + 0,04t3 (расстояние - в метрах, время - в секундах). Найти скорость и ускорение точки в моменты времени tj = 0 и <2=5 с. Каковы средние значения скорости и ускорения за первые 5 с движения?
111. По небольшому куску мягкого железа, лежащему на наковальне массой гщ = 300 кг, ударяет молот массой = 8 кг. Определить к.п.д. удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
141. Определить работу растяжения двух соединенных последовательно пружин жесткостями к] = 400 Н/м и кг = 400 Н/м, если первая при этом растянулась на = 2 см.
142. Нить с привязанными к ее концам грузами массами 50 г и = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции I блока, если под действием силы тяжести грузов он получил угловое ускорение е = 1,5 рад/с2. Трением и проскальзыванием нити по блоку пренебречь.
143. Точка совершает простые гармонические колебания, уравнение которых х = A sin cot, где А = 5 см, со = 2 с"1. В момент времени, когда точка обладала потенциальной энергией Wp = 0,1 мДж, на нее действовала возвращающая сила F = 5 нН. Найти этот момент времени tj.
201. Определить внутреннюю энергию 2 моль водорода, а также среднюю кинетическую энергию поступательного и вращательного движения одной молекулы этого газа при температуре 7°С.
202. При изобарическом расширении двухатомного газа была совершена работа 156,8 Дж. Какое количество теплоты было сообщено газу?
251. Объем аргона, находящегося при давлении 80 кПа, увеличивается от 1 л до 2 л. Найти изменение внутренней энергии газа в двух случаях: при изобарном и при адиабатическом расширении
газа.
271 Найти среднюю продолжительность свободного пробега молекул кислорода при температуре -23°С и давлении 100 кПа. Считать эффективный диаметр молекулы кислорода равным 0,27 нм.
10048_bntu_120_v2
102Материальная точка движется по окружности радиуса 80 см согласно уравнению S = 10t - 0,113 (расстояние - в метрах, время - в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения точки в момент времени 2 с.
132 Шар массой 3 кг движется со скоростью v =2 м/с и сталкивается с покоящимся шаром массой = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
142 Из шахты глубиной 600м поднимают клеть массой mi = 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия подъемного устройства?
152 На скамье Жуковского сидит человек и держит на вытянутых руках гири массой m = 5 кг каждая. Расстояние от каждой гири до оси скамьи I = 70 см. Скамья вращается с частотой щ = 1 с-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до 12 = 20 см? Момент инерции человека и скамьи (вместе) относительно оси I = 2,5 кгм2.
172 Определить частоту v простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости
232 Средняя кинетическая энергия вращательного движения молекулы кислорода в сосуде равна 5-10-21 Дж, а кинетическая энергия поступательного движения всех молекул этого газа составляет 4,5 кДж. Вычислить температуру и количество кислорода в сосуде.
242 При изотермическом расширении 2 кг азота при температуре 7 “С его объем увеличился в 2 раза. Определить работу, совершенную газом при расширении, изменение внутренней энергии и количество теплоты, полученное газом в этом процессе.
252 Определить молярную массу двухатомного газа и его удельные теплоемкости ср и cv, если известно, что разность последних равна 260 Дж/(кг-К). Вычислить также молярные теплоемкости этого газа Ср и С¥.
272 Определить среднюю длину свободного пробега и число соударений за 1 с, проходящих между всеми молекулами водорода, находящимися в сосуде объемом 1 л при температуре 27°С и давлении 10 кПа. Считать эффективный диаметр молекулы водорода равным 0,23 нм.
10049_bntu_120_v3
103 Точка движется по прямой согласно уравнению х = 6t-t3/8 (м). Определите среднюю скорость движения точки в интервале времени от t1 = 2 с до t2 = 6 с, скорость и ускорение точки в момент времени t2 = 6 с.
133 Молот массой m = 5 кг, двигаясь со скоростью v = 4 м/с, ударяет по железному изделию, лежащему на наковальне. Масса наковальни с изделием равна М = 95 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на ковку (деформацию) изделия. Чему равен к.п.д. процесса ковки при данных условиях?
143 Пружина жесткостью к = 500 Н/м сжата силой F = 100 Н. Определить работу А внешней силы, дополнительно сжимающей пружину еще на А1 = 2 см.
153 На скамье Жуковского сидит человек и держит в руках стержень вертикально параллельно оси скамьи. Скамья с человеком вращается с угловой скоростью cot = 4 рад/с. С какой угловой скоростью га2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи 1 = 5 кг м2. Длина стержня 1 = 1,8 м; масса ш = 6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
173 Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
233 Средняя кинетическая энергия поступательного движения молекулы кислорода равна 7,25-10 2! Дж, а кинетическая энергия всех молекул этого газа в сосуде составляет 364 Дж. Вычислить температуру и массу газа в сосуде.
243 Двухатомному газу сообщено 2,093 кДж теплоты. Газ расширяется изобарически. Найти работу расширения газа и изменение его внутренней энергии.
253 Трехатомный газ под давлением 240 кПа и температуре 20°С занимает объем 10 л. Определить теплоемкость этого газа при постоянном давлении и при постоянном объеме.
10050_bntu_120_v4
104 Движения двух материальных точек выражается уравнениями: Xj = 20 + 2t -4t2 (м) и х2 = 2 + 21 +0,5t2 (м). В какой момент времени скорости этих материальных точек будут одинаковыми? Чему равны скорости и ускорения точек в этот момент?
134 Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью Vi = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью V2 = 580 м/с. С какой скоростью откатилось при этом орудие?
144 Две пружины жесткостью к) = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации А1 = 4 см.
154 На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой щ = 8 мин ', стоит человек массой mj = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой п2=10мин-1. Определить массу ш2 платформы. Момент инерции человека рассчитывать, как для материальной точки,
174 Определить период Т колебаний математического маятника, если модуль его максимального перемещения Дг = 18 см и максимальная скорость Vmax= 16 СМ/с.
234 Средняя кинетическая энергия вращательного движения молекулы кислорода равна 3,96-10“21 Дж, а кинетическая энергия вращательного движения всех молекул этого газа в сосуде составляет 477 Дж. Определить температуру и количество кислорода в сосуде, а также массу одной молекулы кислорода
244 Двухатомный идеальный газ расширяется изотермически от объема 100 л до объема 300 л. Конечное давление газа равно 200 кПа. Определить изменение внутренней энергии газа, совершенную им при этом работу и количество полученного газом тепла.
254 Определить показатель адиабаты идеального газа, который при температуре 77°С и давлении 0,4 МПа занимает объем 300 л и имеет теплоемкость при постоянном объеме 857 Дж/К. Найти также число степеней свободы молекул данного газа.
Определить диффузию и динамическую вязкость гелия, находящегося при температуре -73°С и давлении 10кПа. Считать эффективный диаметр молекулы гелия равным 0,19 нм
10051_bntu_120_v5
105 Зависимость пройденного телом пути S от времени t дается уравнением S = At-Bt2 +С13(м), где А = 2 м/с, В = 3 м/с2, С = 4 м/с3. Найти: 1) зависимость скорости v и ускорения а от времени t; 2) расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения,
135 Шар массой, движущийся горизонтально с некоторой скоростью vb столкнулся с неподвижным шаром массой г. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму?
145 Какую нужно совершить работу, чтобы пружину жесткостью к = 800 Н/м, сжатую на х = 6 см, дополнительно сжать на Ах = 8 см?
155 На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой = 6 кг стоит человек массой ш2 = 60 кг. С какой угловой скоростью га начнет вращаться скамья, если человек поймает летящий на него мяч массой щ = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии г = 0,4 м от оси скамьи. Скорость мяча v = 5 м/с.
175 Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с2, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.
235 Найти полную кинетическую энергию 200 г аммиака (NH3) при температуре 27°С, а также среднюю кинетическую энергию вращательного движения молекулы этого газа при тех же условиях.
245 Работа изотермического расширения 10 г некоторого газа, в результате которого его объем удвоился, оказалась равной 575 Дж. Найти среднеквадратичную скорость молекул газа. Вычислить также кинетическую энергию поступательного движения всех молекул данного газа после расширения.
255 В закрытом сосуде объемом 2 л при нормальных условиях содержатся одинаковые массы азота и аргона. Какое количество теплоты надо сообщить этой газовой смеси, чтобы нагреть ее на 100°С?
275 Найти динамическую вязкость воздуха при температуре 100°С и нормальном давлении, если при нормальных условиях она равна 17,2 мкПа с.
10052_bntu_120_v6
106 Зависимость пройденного телом пути S от времени t дается уравнением S = A-Bt + Ct2 (м), где А = 6м, В = 3м/с, С = 2 м/с2. Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 до 4 с, скорость и ускорение в момент времени = 4 с.
136 Человек массой 60 кг. бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее, 1) С какой скоростью станет двигаться тележка?
1) С какой скоростью будет двигаться тележка, если человек бежал ей навстречу?
146 С какой скоростью двигался вагон массой 20 т, если при ударе о стенку каждый буфер сжался на 10 см? Известно, что пружина каждого из буферов сжимается на 1 см под действием силы в 9,8-103 Н.
156 Горизонтальная платформа массой m = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой п = 8 мин'1. Человек массой т2 = 70 кг стоит при этом на краю платформы. С какой угловой скоростью со начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым однородным диском, а человека - материальной точкой.
176 Шарик массой m = 60 г колеблется с периодом Т = 2 с. В начальный момент времени смещение шарика х = 4,0 см и он обладает энергией Е = 0,02 Дж. Записать уравнение гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
236 Вычислить кинетическую энергию вращательного движения молекул, содержащихся в 440 г углекислого газа при температуре 80°С, и их полную кинетическую энергию. Определить также массу одной молекулы углекислого газа.
246 Определить количество теплоты, которое надо сообщить кислороду объемом 50 л при его изохорном нагревании, чтобы давление газа повысилось на 0,5 МПа.
256 Определить удельную теплоемкость Су смеси газов, содержащей 5 л водорода и З л гелия. Газы находятся при одинаковых условиях.
10053_bntu_120_v7
107 Зависимость пройденного телом пути S от времени t дается уравнением S = А + Bt + Ct2 (м), где А = 3 м, В = 2 м/с и С = 1 м/с2. Найти среднюю скорость и среднее ускорение тела за первую, вторую и третью секунды его движения.
137 Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Какую скорость получит вагон, если: 1) вагон стоял неподвижно, 2) вагон двигался со скоростью 36 км/ч в направлении, что и снаряд, 3) вагон двигался со скоростью 36 км/ч в направлении, противоположном движению снаряда?
147 Тонкий длинный стержень массой 300 г и длиной 50 см вращается с угловой скоростью 10 с'1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найти угловую скорость, если в процессе вращения в той же плоскости стержень переместился так, что ось вращения пройдет через конец стержня.
157 Определить скорость v распространения волн в упругой среде, если разность фаз Дер колебаний двух точек, отстоящий друг от друга на Ах = 15 см, равна я/2. Частота колебаний v = 25 Гц.
237 Внутренняя энергия 1 моль некоторого двухатомного газа равна 6 кДж. Вычислить среднюю кинетическую энергию вращательного движения одной молекулы этого газа, считая его идеальным.
247 Двухатомный газ, находящийся при давлении 2 МПа и температуре 27°С, сжимается адиабатически так, что его объем уменьшается в 2 раза. Найти температуру и давление газа после сжатия.
257 Определить показатель адиабаты частично диссоциировавшего на атомы азота, степень диссоциации которого а = 0,4.
10054_bntu_120_v8
108 Зависимость пройденного телом пути S от времени t дается
уравнением S = A + Bt + Ct2 +Dt3(M), где С = 0,14 м/с2 и D = = 0,01 м/с3. 1) Через сколько времени после начала движения ускорение тела будет равно 1 м/с2? 2) Чему равно среднее ускорение тела за этот промежуток времени?
138 Граната, летящая со скоростью 10 м/с, разорвалась на два осколка. БбльшиЙ осколок, масса которого составляла 60% массы всей гранаты, продолжал двигаться в прежнем направлении, но со скоростью, равной 25 м/с. Найти скорость меньшего осколка.
148 Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью v = 0,6 м/с, остановился, сжав пружину на Д1 = 8 см. Найти общую жесткость к пружин буфера.
158 Платформа в виде диска диаметром D = 3 м и массой mi = 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью coi будет вращаться эта платформа, если по ее краю пройдет человек массой т2 = 70 кг со скоростью v = 1,8 м/с относительно платформы?
178 Поперечная волна распространяется вдоль упругого шнура со скоростью 10 м/с. Период колебаний точек шнура 1 с, амплитуда 1,5 см. Определить длину волны, скорость и ускорение точки, отстоящей от источника колебаний на расстоянии 20 см, в момент времени 5 с.
238 Вычислить кинетическую энергию поступательного и вращательного движения 200 г водорода при нормальных условиях.
248 Некоторый газ совершает процесс, в ходе которого давление р изменяется с объемом V по закону: р = р0ехр [-ct(V-V0)] Па, где р0 = 600 кПа, а = 0,2 м“3, V0 = 2 м3. Найти работу, совершаемую газом при расширении от V1 = 3 м3 до V2 = 4 м.
258 Кислород массой 2 кг занимает объем 1 м3и находился под давлением 0,2 МПа. Газ был нагрет сначала изобарно до объема 3 м\ а затем изохорно до давления 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданное газу.
10055_bntu_120_v9
109 Тело движется прямолинейно под действием постоянной силы 15 Н. Зависимость координаты от времени имеет вид х = 10 - 5t + 2t2 (м). Найти массу тела.
139 Тело массой 1 кг, движущееся горизонтально со скоростью 1 м/с, догоняет второе тело 0,5 кг и неупруго сталкивается с ним. Какую скорость получат тела, если: 1) второе тело стояло неподвижно; 2) второе тело двигалось со скоростью 0,5 м/с в том же направлении, что и первое тело; 3) второе тело двигалось со скоростью 0,5 м/с в направлении, противоположном направлению движения первого тела.
149 Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на = 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
159 Какой скоростью должен обладать шар, катящийся без скольжения, чтобы подняться по наклонной плоскости, составляющей с горизонтом угол 30°, на высоту 2 м, если сила сопротивления равна 0,2 веса шара? Чему равно время подъема?
179, Определить скорость распространения волн в упругой среде, если разность фаз колебаний двух точек среды, отстоящих друг от друга на расстоянии 20 см, равна л/3. Частота колебаний 50 Гц.
239 Найти внутреннюю энергию 20 г кислорода при температуре 10°С. Какая энергия приходится на долю поступательного движения молекул этого газа, а какая - на долю вращательного движения. Вычислить также массу молекулы кислорода.
249 Идеальный двухатомный газ, находящийся при температуре 0°С, подвергаю! двум независимым процедурам адиабатического сжатия. В результате первого сжатия объем газа уменьшается в 10 раз. В результате другого сжатия (при прежних начальных условиях) давление газа увеличивается в 10 раз. Определить температуру газа в результате каждого из этих двух процессов.
259 Плотность некоторого двухатомного газа при нормальных условиях равна 1,43 кг/м. Найти удельные теплоемкости Ср и Су этого газа. Определить также среднеквадратичную скорость молекул этого газа при тех же условиях.
279 При каком давлении средняя длина свободного пробега молекул кислорода равна 125 см, если температура газа 47°С? Эффективный диаметр молекулы кислорода 0,27 нм. Чему равна теплопроводность кислорода при таких условиях?
10056_bntu_120_v10
110 Тело массой 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути S от времени t дается уравнением S = А - Bt + Ct2 - Dt3 (м), где С = 5м/с2 и D=1m/c3. Найти силу, действующую на тело в конце первой секунды движения.
140 Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. Найти, на какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения коньков о лед равен 0,02.
150 Определить работу растяжения двух соединенных последовательно пружин жесткостями к1 = 400 Н/м и к2 = 250 Н/м, если первая пружина при этом растянулась на = 2 см.
160 Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами = 0,3 кг и = 0,7 кг. Определить силы натяжения T1 и Т2 нити по обе стороны блока.
180 Волны в упругой среде распространяются со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 3 м от источника колебаний, через 4 с от начала колебаний? Период колебаний 1 с, амплитуда колебаний 2 см
240 Найти полную кинетическую энергию всех молекул двухатомного газа, находящегося в сосуде объемом 2 л под давлением 150 кПа.
250 Кислород занимает объем V) =! mj и находится под давлением р1=200кПа. Газ нагрели сначала изобарно до объема V2 = 3 м3, а затем изохорно до давления р2 = 500 кПа. Построить график процесса и найти: 1) изменение внутренней энергии газа; 2) совершенную им работу; 3) количество теплоты, переданное газу.
260 Вычислить удельные теплоемкости газа ср и cv, зная, что его молярная масса равна 4 г/моль, а показатель адиабаты для него равен 1,67. Определить также молярные теплоемкости Ср и Cv данного газа.
10057_bntu_2882k1_v1
101. Вагон движется равнозамедленным с отрицательным ускорением –0,5 м/с2. Начальная скорость вагона 54 км/ч. Через сколько времени и на каком расстоянии от начальной точки вагон остановится?
111 Диск радиусом 20 см вращается согласно уравнению 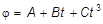 , где А = 3 рад, В = -1 рад/с, С = 0,1 рад/с3. Найти тангенциальное, нормальное и полное ускорения точек на окружность диска в конце десятой секунды после начала вращения.
, где А = 3 рад, В = -1 рад/с, С = 0,1 рад/с3. Найти тангенциальное, нормальное и полное ускорения точек на окружность диска в конце десятой секунды после начала вращения.
121. На барабан массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением нити пренебречь, шнур считать невесомым и нерастяжимым.
131. Определить частоту гармонических колебаний диска радиусом 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
141 Котел объемом 20 л содержит углекислый газ массой 500 г под давлением 1,3 МПа. Определить температуру газа.
151 Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул гелия и азота при температуре 270С. 161 Определить полную энергию всех молекул 100 г каждого из газов.
В сосуде объемом 10 л находится кислород (О 2) под давлением 105 Па. Стенки сосуда могут выдержать внутреннее давление до 106 Па. Газ идеальный, СP / СV =1,4. Определить, какое максимальное количество теплоты можно сообщить газу в этом сосуде.
171 Определить КПД цикла, имеющего на диаграмме Т, S вид, изображенный на рис. 1.8. t 1=6500С, t 2=2500С.
10058_bntu_2882k1_v2
102 Зависимость пройденного телом пути S от времени t дается уравнением S=A+Bt+Сt2+Dt3 Через сколько времени после начала движения ускорение тела будет равно a. Чему равно среднее ускорение тела за этот промежуток времени?
112 Шайба, пущенная по поверхности льда с начальной скоростью 20 м/с, остановилась через 40 с. Найти коэффициент трения шайбы о лед.
122 Маховое колесо, имеющее момент инерции 245  , вращается, делая 20 oб/с. Через минуту после того, как на его перестал действовать вращающий момент, оно остановилось. Найти: а) момент сил трения; б) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
, вращается, делая 20 oб/с. Через минуту после того, как на его перестал действовать вращающий момент, оно остановилось. Найти: а) момент сил трения; б) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
132. Определить возвращающую силу в момент времени 0,2 с и полную энергию точки массой 20 г, совершающей гармонические колебания согласно уравнению  , где А = 15 см;
, где А = 15 см;  .
.
Поиск по сайту: