АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм 2.2. Расчет эмпирического корреляционного отношения

Читайте также:
  1. I. Расчет накопительной части трудовой пенсии.
  2. I. Расчет производительности технологической линии
  3. I. Расчет размера страховой части трудовой пенсии.
  4. I.2.4. Алгоритм симплекс-метода.
  5. I.Диагностика самоотношения.
  6. II. 4.1. Алгоритм метода ветвей и границ
  7. II. Определяем годовые и расчетные часовые расходы газа на бытовое и коммунально - бытовое потребление для населенного пункта
  8. II. Расчетная часть задания
  9. III. Расчет процесса в проточной части ЦВД после камеры смешения.
  10. IV. Расчет продуктов сгорания топлива.
  11. IV. ТИПОВОЙ ПРИМЕР РАСЧЕТОВ.
  12. LU – алгоритм нахождения собственных значений для несимметричных задач

1. В ячейке, выделенной для общей дисперсии (А63), перед формулой поставить знак равенства «=»;

2. Enter;

3. В ячейке, выделенной для средней из внутригрупповых дисперсий (В63), перед формулой поставить знак равенства «=»;

4. Enter;

►Примечание. В случае если при выполнении вычисления в ячейке В63 выдается сообщение "Ошибка в формуле", то разделительный знак «,» между аргументами функции СУМПРОИЗВ(Д1,Д2) необходимо заменить на знак «;».

5. В ячейке, выделенной для значения межгрупповой (факторной) дисперсии (С63), перед формулой поставить знак равенства «=»;

6. Enter;

7. В ячейке, выделенной для эмпирического корреляционного отношения (D63), перед формулой поставить знак равенства «=»;

8. Enter.

Результат работы алгоритма 2.2 для демонстрационного примера представлен в табл.2.4–ДП.

  A B C D
  Таблица 2.4–ДП
  Показатели дисперсий и эмпирического корреляционного отношения
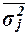
  Общая дисперсия Средняя из внутригрупповых дисперсий Межгрупповая дисперсия Эмпирическое корреляционное отношение η
  1450,288889 551,6853535 898,6035354 0,787148735

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)