Деление пополам

Отчет по лабораторным работам

по курсу: «Методы оптимизации»

Студент: _________ (Степанов В.В.) Группа ИУ6-52.

Руководитель: __________ (Грибов А.Ф.)

Москва, 2011

Одномерная минимизация

Поразрядный поиск

Можно усовершенствовать метод перебора с целью уменьшения количества значений F(x), которые необходимо находить в процессе минимизации. Во-превых, если оказывается, что F(xi)<= F(x[i+1]), то отпадает необходимость вычислять F(x) в точках x[i+2], x[i+3] и т.д.. Во-вторых, разумно было бы сначала определить отрезок, содержащий оптимальную точку, грубо, т.е. найти точку xm с небольшой точностью, а затем искать ее на этом отрезке с меньшим шагом дискретизации, повышая точность. Эти возможности улучшения и реализованы в методе поразрядного поиска. В этом методе перебор точек отрезка происходит сначала с шагом d=x[i+1]-xi > eps до тех пор, пока не выполнится условие F(xi) < F(x[i+1]) или пока очередная из точек не совпадет с концом отрезка. После этого шаг уменьшается (обычно в 4-5 раза), и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения F(x) снова не перестанут уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит eps.

Исходныйкод.

#include"stdafx.h"

#include<math.h>

#include<iostream>

#include<conio.h>

usingnamespace std;

float fun(float x)

{

return (x+3)*(x+3)-2;

}

int _tmain(int argc, _TCHAR* argv[])

{

setlocale(LC_ALL,"Russian");

float a,b,eps,min_i,min_f;

int n=0;

cout<<"Координата левого края ";

cin>>a;

cout<<"Координата правого края ";

cin>>b;

cout<<"Точность";

cin>>eps;

float k=10000;

float ab=(b-a)/k;

b=a+ab;

while(eps<abs(b-a))

{

min_f=fun(a+ab);

min_i=0;

for(int i=1;i<(k-1);i++)

{

if (min_f>fun(a+(i)*ab))

{

min_i=i;

min_f=fun(a+(i)*ab);

}

}

if(n==0)

{

a=a+min_i*ab;

n=1;

}

else

{

b=a+min_i*ab;

n=0;

}

ab=(b-a)/k;

cout<<" a = "<<a<<" b = "<<b<<" ab = "<<ab<<" fun = "<<fun(a+(b-a)/2)<<'\n';

}

getch();

return 0;

}

Деление пополам

Рассмотрим функцию F, которую требуется минимизировать на интервале [a1, b1]. Предположим, что F строго квазивыпукла. Очевидно, что наименьшее число вычислений значений функции, которые необходимы для сокращения интервала неопределенности, равно двум. Одной из стратегий является выбор этих двух точек симметрично на расстоянии eps>0 от середины интервала. Здесь число eps настолько мало, чтобы длина нового интервала неопределенности eps+(b1-a1)/2 являлась достаточно близкой к теоретическому значению (b1-a1)/2, и в то же время такое, чтобы значение функции в этих двух точках были различимы.

Исходныйкод.

#include"stdafx.h"

usingnamespace std;

float fun(float x)

{

return x*x;

}

void _tmain()

{

float a,b,x1,x2,eps,d;

d=0.001;

setlocale(LC_ALL,"Russian");

cout<<"ВВедитеточность: ";

cin>>eps;

cout<<"Началоотрезка: ";

cin>>a;

cout<<"Конецотрезка: ";

cin>>b;

while ((b-a) >= eps) // пока длина отрезка [a,b] >= заданной точности

{

cout<<"Отрезок: "<<a<<" "<<b<<"\n";

getch();

if (a>=0)//если а положительное

{

x1=a+((b-a)/2)-d;

x2=a+((b-a)/2)+d;

}

else

{

if (b>=0)//еслиb>=0иa<=0

{

x1=((b+a)/2)-d;

x2=((b+a)/2)+d;

}

else//еслиb<=0иa<=0

{

x1=b+((a-b)/2)-d;

x2=b+((a-b)/2)+d;

}

}

fun(x1)<=fun(x2)?b=x1:a=x1; //

}

a=x1;b=x2;

b=a+(x2-x1)/2;

cout<<"*********************************\n";

cout<<"Результат: \n min: "<<b<<"\n";

cout<<"f(min)"<<fun(b)<<"\n";

getch();

}

Тестирование для функции .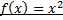

ВВедите точность: 0.01

Начало отрезка: -2

Конец отрезка: 2

Отрезок: -2 2

Отрезок: -0.0001 2

Отрезок: -0.0001 0.99985

Отрезок: -0.0001 0.499775

Отрезок: -0.0001 0.249738

Отрезок: -0.0001 0.124719

Отрезок: -0.0001 0.0622094

Отрезок: -0.0001 0.0309547

Отрезок: -0.0001 0.0153273

*********************************

Результат:

min: 0.00761367

f(min)5.7968e-005

Поиск по сайту: