Метод деформированного симплекса

Правильным симплексом в пространстве En называется множество из n+1 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса.

В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, а в E3 - правильного тетраэдра. Если x0 - одна из вершин правильного симплекса в En, то координаты остальных n вершин x1,..., xn можно найти, например, по формулам:

xj0 + d1, i!= j,

xji ={.....................................................................(1)

xj0 + d2, i=j,

где d1 = a(sqrt(n+1) - 1) / n*sqrt(2), d2 = a(sqrt(n+1) + n - 1) / n*sqrt(2), a - длинаребра.

Вершину x0 симплекса, построенного по формулам (1), будем называть базовой. В алгоритме симплексного метода используется следующее важное свойство правильного симплекса. По известному симплексу можно построить новый симплекс путем отражения какой-либо вершины, например, xk симметрично относительно центра тяжести xc остальных вершин симплекса. Новая и старая вершины y и xk связаны соотношением: (y+ xk)/2 = xс, где xc = (1/n)Sum(xi) для всех i!=k. В результате получаем новый симплекс с тем же ребром и вершинами y=2xс-xk, xi, i=0,...,n, i!=k. Таким образом происходит перемещение симплекса в пространстве. На рисисунке представлена иллюстрация этого свойства симплекса для двумерной области.

Построение нового симплекса в Е2 отражением точки х2.

Поиск точки минимума функции f(x) с помощью правильных симплексов производится следующим образом. На каждой итерации сравниваются значения функции в вершинах симплекса. Затем проводится описанная выше процедура отражения для той вершины, в которой f(x) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. Если же попытка отражения не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину x0 старого симплекса, в которой функция принимает минимальное значение. Поиск точки минимума f(x) заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.

Алгоритм минимизации по правильному симплексу можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения. А именно, положение новой вершины y вместо вершины xn, соответствующей наибольшему значению функции, находится сравнением и выбором наименьшего среди значений целевой функции в точках:

z1= xc - a(xc - xn), 0<a<1;

z2 = xc + a(xc - xn), 0<a<1;............................................................(2)

z3 = xc + b(xc - xn), b приближенно равно 1;

z4 = xc + g(xc - xn), g<1.

Геометрическая иллюстрация этих процедур для двумерного пространства приведена на рисунке.

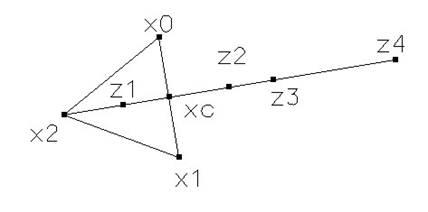
Пробные точки z1, z2, z3, z4 для перехода к новому симплексу

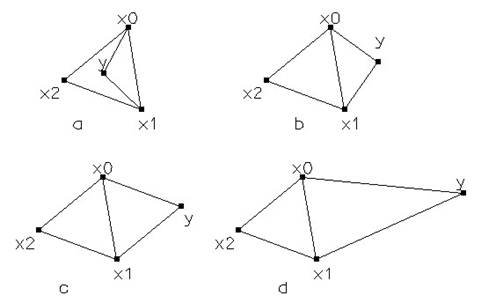
Новые симплексы полученные в результате процедуры сжатия (a,b); отражения (c); растяжения (d)

Так как величина a принадлежит интервалу (0;1), то выбор точек z1 и z2 соответствует сжатию симплекса; b приближенно равно 1, поэтому выбор точки z3 соответствует отражению, а g>1 и выбор точки z4 приводит к растяжению симплекса.

Отметим, что при деформациях утрачивается свойство правильности исходного симплекса.

На практике хорошо зарекомендовал себя следующий набор параметров a=1/2, b=1, g=2.

Исходный код.

#include"stdafx.h"

usingnamespace std;

float func(float x, float y)

{

return 100*(y-x*x)*(y-x*x)+(1-x)*(1-x);

}

bool shodimost (float fh, float fl, float fg, float eps)

{

float f0=(fh+fl+fg)/3;

float disp=(fh-f0)*(fh-f0);

disp=disp+(fl-f0)*(fl-f0);

disp=disp+(fg-f0)*(fg-f0);

disp=sqrt(disp/3);

if (disp < eps) return 1;

elsereturn 0;

}

int _tmain(int argc, _TCHAR* argv[])

{

float x[3],y[3],f[3]; // начальные точки

float h[2],l[2],g[2],fh,fl,fg,c[2],z3[2],fz3,z4[2],fz4,eps,z1[2],fz1;

eps=0.00001;

printf("Vvedite koordinati tochki 1: ");scanf_s("%f %f",&x[0],&y[0]);

printf("Vvedite koordinati tochki 2: ");scanf_s("%f %f",&x[1],&y[1]);

printf("Vvedite koordinati tochki 3: ");scanf_s("%f %f",&x[2],&y[2]);

f[0]=func(x[0],y[0]);

f[1]=func(x[1],y[1]);

f[2]=func(x[2],y[2]);

if (f[0]>f[1])

if (f[1]>f[2])

{ h[0]=x[0];h[1]=y[0];fh=f[0];

l[0]=x[2];l[1]=y[2];fl=f[2];

g[0]=x[1];g[1]=y[1];fg=f[1];}

else

if (f[2]>f[0])

{ h[0]=x[2];h[1]=y[2];fh=f[2];

l[0]=x[1];l[1]=y[1];fl=f[1];

g[0]=x[0];g[1]=y[0];fg=f[0];}

else { h[0]=x[0];h[1]=y[0];fh=f[0];

l[0]=x[1];l[1]=y[1];fl=f[1];

g[0]=x[2];g[1]=y[2];fg=f[2];}

else

if (f[0]>f[2])

{ h[0]=x[1];h[1]=y[1];fh=f[1];

l[0]=x[2];l[1]=y[2];fl=f[2];

g[0]=x[0];g[1]=y[0];fg=f[0];}

else

if (f[2]>f[1])

{ h[0]=x[2];h[1]=y[2];fh=f[2];

l[0]=x[0];l[1]=y[0];fl=f[0];

g[0]=x[1];g[1]=y[1];fg=f[1];}

else { h[0]=x[1];h[1]=y[1];fh=f[1];

l[0]=x[0];l[1]=y[0];fl=f[0];

g[0]=x[2];g[1]=y[2];fg=f[2];}

while (shodimost(fh,fl,fg,eps)==0)

{

c[0]=(l[0]+g[0])/2;

c[1]=(l[1]+g[1])/2;

z3[0]=c[0]+c[0]-h[0];

z3[1]=c[1]+c[1]-h[1];

fz3=func(z3[0],z3[1]);

if (fz3<fl)

{ //правильный выбор.пробуем еще раз в ту же сторону

z4[0]=c[0]+2*(c[0]-h[0]);

z4[1]=c[1]+2*(c[1]-h[1]);

fz4=func(z4[0],z4[1]);

if (fz4<fl) {h[0]=z4[0];h[1]=z4[1];fh=fz4;} //правильный выбор - заменяем наибольшую вершину

else {h[0]=z3[0];h[1]=z3[1];fh=fz3;} //замена на предыдущую точку

}

else

if (fz3>fg) //пробная точка не наименьшая

if (fz3>fh) //неправильное направление

{

z1[0]=c[0]-(c[0]-h[0])/2; //двигаемся назад

z1[1]=c[1]-(c[1]-h[1])/2;

fz1=func(z1[0],z1[1]);

if (fz1>fh) //если все равно больше, то:

{

h[0]=(h[0]+l[0])/2;

h[1]=(h[1]+l[1])/2;

g[0]=(g[0]+g[0])/2;

g[1]=(g[1]+g[1])/2;

f[0]=func(l[0],l[1]); f[1]=func(g[0],g[1]); f[2]=func(h[0],h[1]);

x[0]=l[0]; x[1]=g[0]; x[2]=h[0];

y[0]=l[1]; y[1]=g[1]; y[2]=h[1];

}

else {h[0]=z1[0];h[1]=z1[1];fh=fz1;}

}

else {h[0]=z3[0];h[1]=z3[1];fh=fz3;}

else {h[0]=z3[0];h[1]=z3[1];fh=fz3;}

f[0]=fl; f[1]=fg; f[2]=fh;

x[0]=l[0]; y[0]=l[1];

x[1]=g[0]; y[1]=g[1];

x[2]=h[0]; y[2]=h[1];

if (f[0]>f[1])

if (f[1]>f[2])

{ h[0]=x[0];h[1]=y[0];fh=f[0];

l[0]=x[2];l[1]=y[2];fl=f[2];

g[0]=x[1];g[1]=y[1];fg=f[1];}

else

if (f[2]>f[0])

{ h[0]=x[2];h[1]=y[2];fh=f[2];

l[0]=x[1];l[1]=y[1];fl=f[1];

g[0]=x[0];g[1]=y[0];fg=f[0];}

else { h[0]=x[0];h[1]=y[0];fh=f[0];

l[0]=x[1];l[1]=y[1];fl=f[1];

g[0]=x[2];g[1]=y[2];fg=f[2];}

else

if (f[0]>f[2])

{ h[0]=x[1];h[1]=y[1];fh=f[1];

l[0]=x[2];l[1]=y[2];fl=f[2];

g[0]=x[0];g[1]=y[0];fg=f[0];}

else

if (f[2]>f[1])

{ h[0]=x[2];h[1]=y[2];fh=f[2];

l[0]=x[0];l[1]=y[0];fl=f[0];

g[0]=x[1];g[1]=y[1];fg=f[1];}

else { h[0]=x[1];h[1]=y[1];fh=f[1];

l[0]=x[0];l[1]=y[0];fl=f[0];

g[0]=x[2];g[1]=y[2];fg=f[2];}

}

printf("\nZnachenie funkcii: %3.5f\n",fl);

printf("Tochka minimuma: (%3.5f,%3.5f)",l[0],l[1]);

getch();

return 0;

}

Поиск по сайту: