АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Изложение метода

Читайте также:
  1. I.2.4. Алгоритм симплекс-метода.
  2. II. 4.1. Алгоритм метода ветвей и границ
  3. II. Проблема источника и метода познания.
  4. SWOT-анализ в качестве универсального метода анализа.
  5. Административными методами можно предотвратить необоснованные расходы (хищение, злоупотребление).
  6. Алгоритм метода
  7. Алгоритм метода ветвей и границ
  8. Алгоритм метода ДФП
  9. Алгоритм метода касательных
  10. Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
  11. Алгоритм метода покоординатного спуска, не использующий одномерной оптимизации.
  12. Алгоритм метода скорейшего спуска решения ЗММ.

Метод штрафных функций относится к группе методов внутренней точки, т.е. он начинает работать с допустимой точки и генерирует последовательность допустимых точек . Метод барьерных функций, наоборот, относится к группе методов внешней точки, он начинает поиск с недопустимой точки и генерирует последовательность недопустимых решений, которая приближается к оптимальному решению извне допустимой области.

Пусть имеется задача минимизировать при ограничениях

,

,

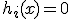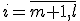
В частности, для искомых функций – ограничений целесообразно использовать барьерную функцию следующего вида:

- непрерывные функции, которые удовлетворяют условиям:

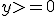, если и 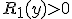, если ,

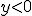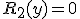, если и , если .

Типичными являются следующие выражения для функций :

,

, где р – целое положительное число.

Далее от исходной задачи переходим кзадачи безусловной оптимизации вспомогательной функции: минимизировать , где - штрафной коэффициент.

Пусть α– непрерывная функция. Обозначим .

Подход, связанный с барьерной функцией состоит в решении задачи вида:

максимизировать 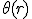при ограничении


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)